Как эквидистантно пересчитать линию (или кривую)?
у меня есть строка l_1 дано с точечным рядом p_1,...,p_n. Теперь я хочу новую строку l_2 С k вопросы: q_1,...,q_k. но для всех i in {1,...,k-1}: abs( q_i - q_i+1 ) = const, т. е. сегментов l_2 равноудалены или униформа.
k >= 2- и
p_1и ценность должна быть вl_2. -
abs( p_i - p_i+1 )не const
одним из решений является аппроксимация линии сплайном, а затем снова подмножество, чтобы иметь равномерную длину тогда сегменты. Могу я сделать лучше? Есть ли для этого код на C++?
Ах, я пропустил конкретную деталь: те q_i должно быть l_1, то есть, либо они находятся на сегментах линии l_1 или они являются образцами точек l_1.
2 ответов
использование параметрической функции
вы можете определить кусочно-параметрическую функцию:
f[t_] := Piecewise[
When x[i] <= t <= x[i + 1]
f[t]= (y[i+1]-y[i]) (t - x[i]) / (x[i+1]-x[i]) + y[i],
For {i, 1 ... N};
затем выберите свои точки q, идеально расположенные меньше минимального p[i+1] - p[i]
наконец, образец f[q]с равными интервалами t.
пример результата:
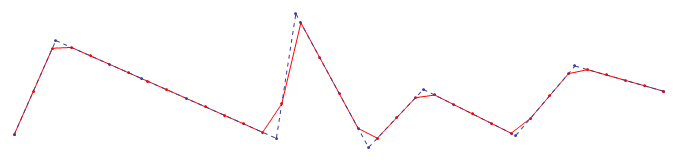
здесь вы можете увидеть эффект уменьшения размера интервала от самого большого до самого маленького в оригинале пример:

вы можете оценить добротность аппроксимации, складывая области (интегрируя) между исходной и повторно отобранной кривыми:
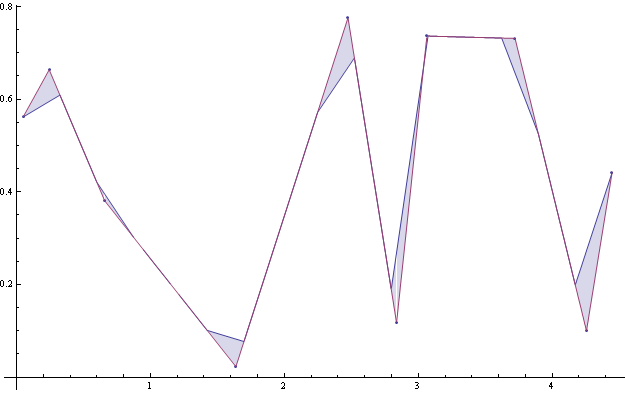
если вы строите интегралы для разных размеров интервалов, вы можете решить, что такое хорошая выборка:
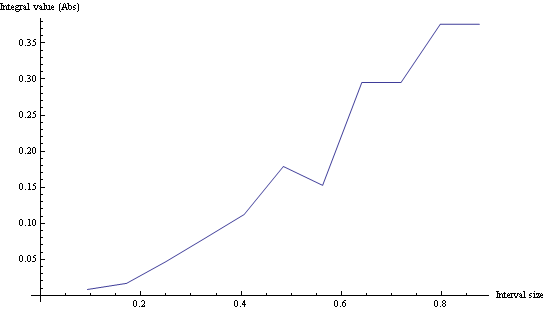
просто для записи, код в Mathematica:
a = 0;
p = Table[{ a = a + RandomReal[], RandomReal[]}, {10}];
f[t_, h_] := Piecewise[Table[{(h[[i + 1, 2]] - h[[i, 2]]) (t - h[[i, 1]]) /
(h[[i + 1, 1]] - h[[i, 1]]) + h[[i, 2]],
h[[i, 1]] <= t <= h[[i + 1, 1]]},
{i, 1, Length[h] - 1}]];
minSeg[h_] := Min[Table[Norm[h[[i, 1]] - h[[i + 1, 1]]], {i, Length[h] - 1}]];
newSegSize[h_] := (h[[Length@h, 1]] - h[[1, 1]])/
Ceiling[(h[[Length@h, 1]] - h[[1, 1]])/minSeg[h]]
qTable = Table[{t, f[t, p]}, {t, p[[1, 1]], p[[Length@p, 1]], newSegSize[p]}];
Edit: ответ на ваш комментарий
прокомментировал код pgm:
a = 0; (* Accumulator to ensure an increasing X Value*)
p = Table[{a = a + RandomReal[],
RandomReal[]}, {10}]; (*Generates 10 {x,y} Rnd points with \
increasing x Value*)
f[t_, h_] := (* Def. a PWise funct:
Example of resulting function:
f[t,{{1,2},{2,2},{3,4}}]
Returns teh following function definition:
Value for Range
2 1<=t<=2
2+2*(-2+t) 2<=t<=3
0 True
*)
Piecewise[
Table[{(h[[i + 1, 2]] -
h[[i, 2]]) (t - h[[i, 1]])/(h[[i + 1, 1]] - h[[i, 1]]) + h[[i, 2]],
h[[i, 1]] <= t <= h[[i + 1, 1]]},
{i, 1, Length[h] - 1}]];
minSeg[h_] := (* Just lookup the min input point separation*)
Min[Table[Norm[h[[i, 1]] - h[[i + 1, 1]]], {i, Length[h] - 1}]];
newSegSize[h_] := (* Determine the new segment size for having
the full interval length as a multiple of the
segment size *)
(h[[Length@h, 1]] - h[[1, 1]])/
Ceiling[(h[[Length@h, 1]] - h[[1, 1]])/minSeg[h]]
qTable = (*Generates a table of points using the PW function *)
Table[
{t, f[t, p]},
{t, p[[1, 1]], p[[Length@p, 1]],newSegSize[p]}];
ListLinePlot[{qTable, p}, PlotStyle -> {Red, Blue}] (*Plot*)
Это зависит от ваших точек линии-каковы они? Если они определяют гладкую линию, то пересчет кубического сплайна является хорошей ставкой.
по сути, если вы делаете точки, равноудаленные, вам нужно определить, что вы хотите видеть между точками - это плавность важнее, чем верность исходной строки? Есть ли ограничение скорости?
насколько я вижу, вы, скорее всего, закончите итерационный процесс здесь, потому что, если ваши исходные точки определяют гладкая линия, не просто вычислить даже длину этой линии, не говоря уже о том, чтобы разделить ее на равные части и определить координаты этих точек.
Если вы используете кубические сплайны, для каждого сплайна вы сможете рассчитать его длину по формуле on статья длины дуги Википедии. Однако это требует от вас интеграции - когда вы делаете численное интегрирование, оно известно как'квадратура'. Для кубического (для вычисления длины отрезок линии между двумя исходными точками), это должно закончиться как взвешенная сумма коэффициентов кубического сплайна - особенно если вы используете гауссову квадратуру.
однако вы, вероятно, могли бы получить разумный ответ, используя кусочно-кубические полиномы (генерировать кубический полином из 2 точек и 2 точек по обе стороны от них) и итерационный алгоритм, который улучшает значения догадки xi, чтобы дать равноудаленные точки. Но это при условии, что вы хотите скорость, а не точность.
