Как генерировать спектрограмму 1D-сигнала в python?
Я не уверен, как это сделать, и я приводил пример, спектрограммы, например, но это в 2D.
У меня есть код, который создает сочетание частот, и я могу забрать их в БПФ, как я могу видите это на спектрограмме? Я понимаю, что частоты в моем примере не меняются со временем; значит ли это, что я увижу прямую линию через спектрограмму?
мой код и вывод изображения:
# create a wave with 1Mhz and 0.5Mhz frequencies
dt = 2e-9
t = np.arange(0, 10e-6, dt)
y = np.cos(2 * pi * 1e6 * t) + (np.cos(2 * pi * 2e6 *t) * np.cos(2 * pi * 2e6 * t))
y *= np.hanning(len(y))
yy = np.concatenate((y, ([0] * 10 * len(y))))
# FFT of this
Fs = 1 / dt # sampling rate, Fs = 500MHz = 1/2ns
n = len(yy) # length of the signal
k = np.arange(n)
T = n / Fs
frq = k / T # two sides frequency range
frq = frq[range(n / 2)] # one side frequency range
Y = fft(yy) / n # fft computing and normalization
Y = Y[range(n / 2)] / max(Y[range(n / 2)])
# plotting the data
subplot(3, 1, 1)
plot(t * 1e3, y, 'r')
xlabel('Time (micro seconds)')
ylabel('Amplitude')
grid()
# plotting the spectrum
subplot(3, 1, 2)
plot(frq[0:600], abs(Y[0:600]), 'k')
xlabel('Freq (Hz)')
ylabel('|Y(freq)|')
grid()
# plotting the specgram
subplot(3, 1, 3)
Pxx, freqs, bins, im = specgram(y, NFFT=512, Fs=Fs, noverlap=10)
show()
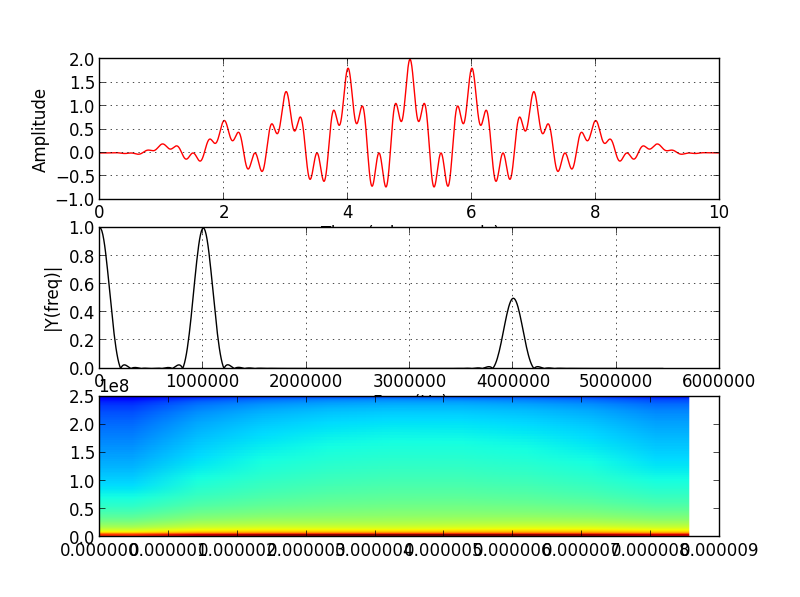
3 ответов
то, что вы технически правильно, но вам просто нужно посмотреть на сигнал с интересным спектрограммы. Для этого вам нужно частота меняются со временем. (И для этого вам нужно много колебаний, так как для установления частоты требуется несколько колебаний, а затем вам нужно много из них, чтобы иметь изменение частоты со временем интересным способом.)
ниже я изменил код как можно меньше, чтобы получить частоту, которая делает что-то интересное (fscale просто увеличивает частоту с течением времени). Я отправляю весь код, чтобы заставить это работать, но я меняю только три из четырех верхних строк.
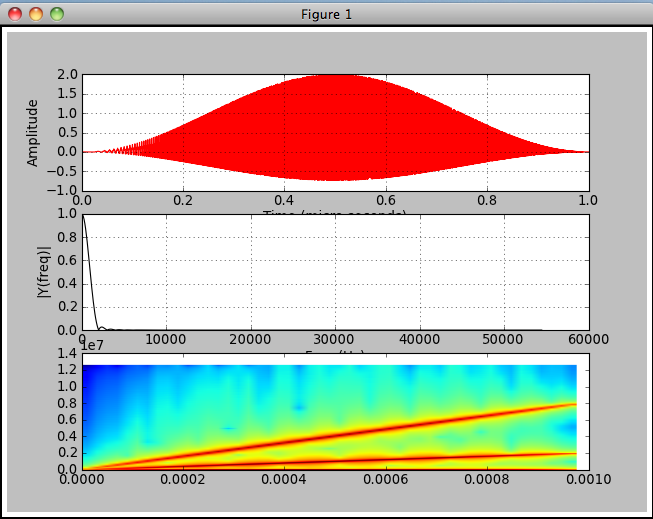
# create a wave with 1Mhz and 0.5Mhz frequencies
dt = 40e-9
t = np.arange(0, 1000e-6, dt)
fscale = t/max(t)
y = np.cos(2 * pi * 1e6 * t*fscale) + (np.cos(2 * pi * 2e6 *t*fscale) * np.cos(2 * pi * 2e6 * t*fscale))
y *= np.hanning(len(y))
yy = np.concatenate((y, ([0] * 10 * len(y))))
# FFT of this
Fs = 1 / dt # sampling rate, Fs = 500MHz = 1/2ns
n = len(yy) # length of the signal
k = np.arange(n)
T = n / Fs
frq = k / T # two sides frequency range
frq = frq[range(n / 2)] # one side frequency range
Y = fft(yy) / n # fft computing and normalization
Y = Y[range(n / 2)] / max(Y[range(n / 2)])
# plotting the data
subplot(3, 1, 1)
plot(t * 1e3, y, 'r')
xlabel('Time (micro seconds)')
ylabel('Amplitude')
grid()
# plotting the spectrum
subplot(3, 1, 2)
plot(frq[0:600], abs(Y[0:600]), 'k')
xlabel('Freq (Hz)')
ylabel('|Y(freq)|')
grid()
# plotting the specgram
subplot(3, 1, 3)
Pxx, freqs, bins, im = specgram(y, NFFT=512, Fs=Fs, noverlap=10)
show()
кроме того, обратите внимание, что полезна только спектрограмма. Если вы можете увидеть хорошую форму волны или спектры, то спектрограмма вероятно не будет интересна: 1) Если форма волны ясна, то вы вероятно не имеете достаточные данные и время над которыми частота и хорошо определена и изменяет достаточно чтобы быть интересным; 2) если полные спектры ясны, у вас, вероятно, недостаточно вариаций частоты для спектрограммы, поскольку спектр в основном представляет собой среднее значение того, что вы видите, меняющееся со временем в спектрограмме.
Если вы действительно хотите увидеть спектрограмму исходного сигнала, вам просто нужно увеличить ось y, чтобы увидеть пики, которые вы ожидаете (обратите внимание, что ось Y спектрограммы равна 2.5e8, должно быть больше, чем в вашем спектре):
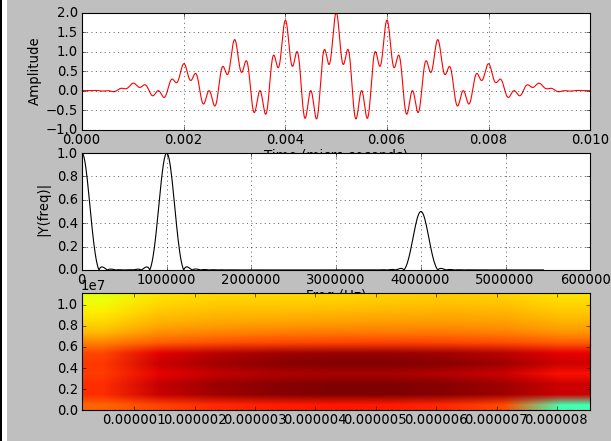
чтобы получить то, что вы после:
1) образец формы волны 1d на частоте коротковолнового диапазона (по крайней мере 5 времен частота своего компонента самой высокой частоты)
2) используйте блоки образцов (мощности 2, такие как 1024,16384 и т. д.) Для вычисления БПФ
3) для каждого спектра постройте вертикальную линию пикселей, цвет которой представляет амплитуду каждой частоты.
4) Повторите шаги 2 и 3 для каждого блока выборок.
в вашем случае сюжет имеет целая радуга цветов, которые не должны присутствовать только с парой очень разных частот. Ваш спектральный график имеет довольно широкие полосы вокруг пиков, но это может быть связано с низкой частотой дискретизации и плавным построением графика.
Я только начинаю на Python 3.6 Спасибо за образец кода спектрограммы!
однако с Python 3.6 я немного боролся, чтобы сделать этот образец кода спектрограммы для работы (вызовы функций и разделение float Я отредактировал код, поэтому теперь он работает на python 3.6 для моих друзей-новичков python.
наслаждайтесь
'''
Original Script for Python 2.7
https://stackoverflow.com/questions/19052324/how-do-i-generate-a-spectrogram-of-a-1d-signal-in-python
Modified in August 2017 for Python 3.6
Python 2.7 two integers / Division generate Integer
Python 3.6 two integers / Division generate Float
Python 3.6 two integers // Division generate integer
'''
import numpy as np
from scipy import fftpack
import matplotlib.pyplot as plt
dt = 40e-9
t = np.arange(0, 1000e-6, dt)
fscale = t/max(t)
y = np.cos(2 * np.pi * 1e6 * t*fscale) + (np.cos(2 * np.pi * 2e6 *t*fscale) * np.cos(2 * np.pi * 2e6 * t*fscale))
y *= np.hanning(len(y))
yy = np.concatenate((y, ([0] * 10 * len(y))))
# FFT of this
Fs = 1 / dt # sampling rate, Fs = 500MHz = 1/2ns
n = len(yy) # length of the signal
k = np.arange(n)
T = n / Fs
frq = k / T # two sides frequency range
frq = frq[range(n // 2)] # one side frequency range
Y = fftpack.fft(yy) / n # fft computing and normalization
Y = Y[range(n // 2)] / max(Y[range(n // 2)])
# plotting the data
plt.subplot(3, 1, 1)
plt.plot(t * 1e3, y, 'r')
plt.xlabel('Time (micro seconds)')
plt.ylabel('Amplitude')
plt.grid()
# plotting the spectrum
plt.subplot(3, 1, 2)
plt.plot(frq[0:600], abs(Y[0:600]), 'k')
plt.xlabel('Freq (Hz)')
plt.ylabel('|Y(freq)|')
plt.grid()
# plotting the specgram
plt.subplot(3, 1, 3)
Pxx, freqs, bins, im = plt.specgram(y, NFFT=512, Fs=Fs, noverlap=10)
plt.show()
