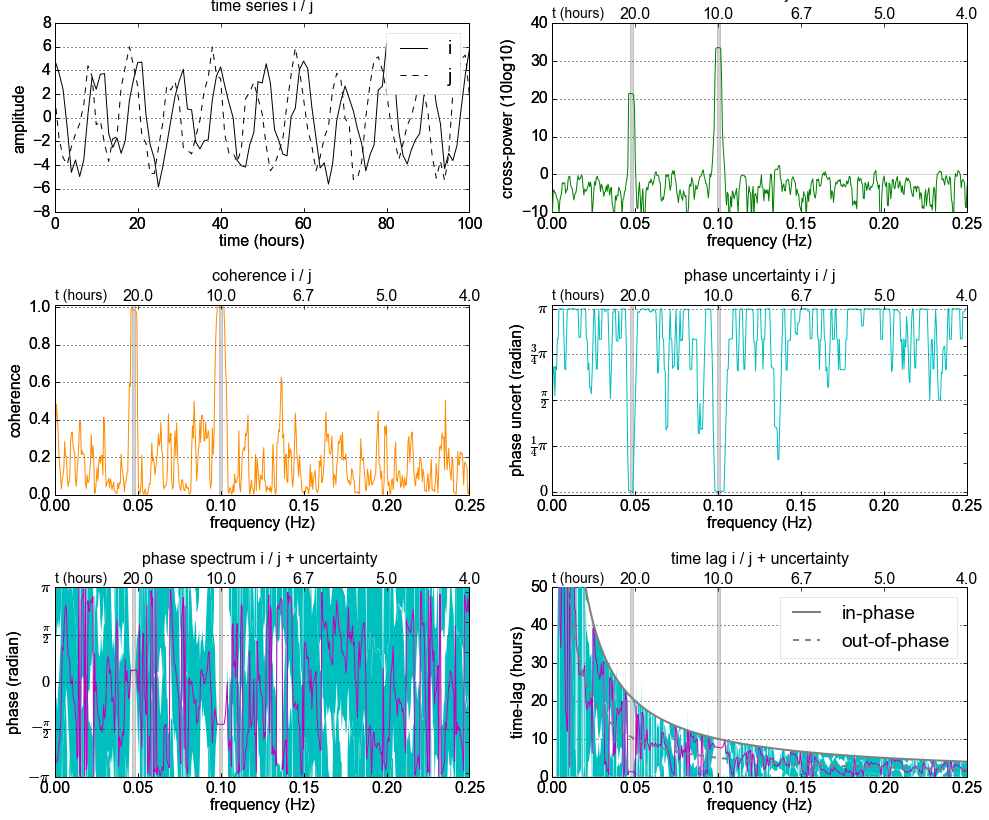
Как использовать кросс-спектральную плотность для вычисления фазового сдвига двух связанных сигналов

У меня есть два сигнала, из которых я ожидаю, что один отвечает на другой, но с определенным фазовым сдвигом.

теперь я хотел бы вычислить когерентность или нормализованную поперечную спектральную плотность, чтобы оценить, есть ли какая-либо причинность между входом и выходом, чтобы узнать, на каких частотах появляется эта когерентность.

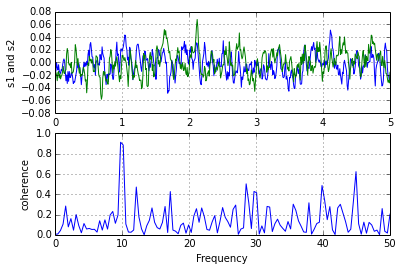
см., например, это изображение (от здесь) который, кажется, имеет высокую когерентность на частоте Десять: enter image description here

теперь я знаю, что могу рассчитать фазовый сдвиг двух сигналов с помощью перекрестной корреляции, но как я могу использовать когерентность (частоты 10) для вычисления фазового сдвига?

код для изображения:

"""
Compute the coherence of two signals
"""
import numpy as np
import matplotlib.pyplot as plt

# make a little extra space between the subplots
plt.subplots_adjust(wspace=0.5)

nfft = 256
dt = 0.01
t = np.arange(0, 30, dt)
nse1 = np.random.randn(len(t))                 # white noise 1
nse2 = np.random.randn(len(t))                 # white noise 2
r = np.exp(-t/0.05)

cnse1 = np.convolve(nse1, r, mode='same')*dt   # colored noise 1
cnse2 = np.convolve(nse2, r, mode='same')*dt   # colored noise 2

# two signals with a coherent part and a random part
s1 = 0.01*np.sin(2*np.pi*10*t) + cnse1
s2 = 0.01*np.sin(2*np.pi*10*t) + cnse2

plt.subplot(211)
plt.plot(t, s1, 'b-', t, s2, 'g-')
plt.xlim(0,5)
plt.xlabel('time')
plt.ylabel('s1 and s2')
plt.grid(True)

plt.subplot(212)
cxy, f = plt.cohere(s1, s2, nfft, 1./dt)
plt.ylabel('coherence')
plt.show()

.
.
EDIT:

для чего это стоит, я добавил ответ, может быть, это правильно, может быть, это неправильно. Я не уверен..

9
cross-correlation matplotlib python signal-processing spectral-density

3 ответов

позвольте мне попытаться ответить на мой собственный вопрос, и, возможно, однажды это может быть полезно для других или функционировать в качестве отправной точки для (нового) обсуждения:

во-первых, вычисления спектральной плотности мощности двух сигналов, 

subplot(121)
psd(s1, nfft, 1/dt)
plt.title('signal1')

subplot(122)
psd(s2, nfft, 1/dt)
plt.title('signal2')

plt.tight_layout()
show()

в результате: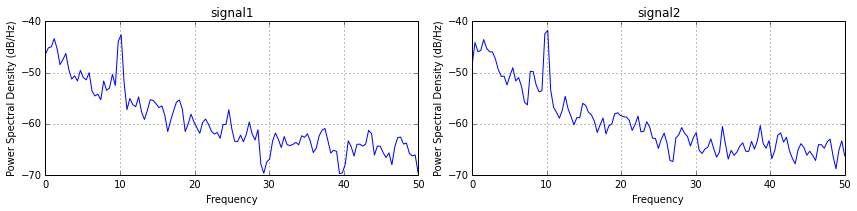enter image description here

во-вторых, вычислите кросс-спектральную плотность, которая является преобразованием Фурье кросс-корреляционной функции:

csdxy, fcsd = plt.csd(s1, s2, nfft, 1./dt)
plt.ylabel('CSD (db)')
plt.title('cross spectral density between signal 1 and 2')
plt.tight_layout()
show()

что дает:

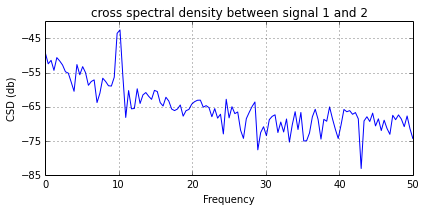
enter image description here

чем используя кросс-спектральную плотность, мы можем рассчитать фазу, и мы можем рассчитать когерентность (которая разрушит фазу). Теперь мы можем комбинировать когерентность и пики, которые поднимаются выше 95% уровня доверия

# coherence
cxy, fcoh = cohere(s1, s2, nfft, 1./dt)

# calculate 95% confidence level
edof = (len(s1)/(nfft/2)) * cxy.mean() # equivalent degrees of freedom: (length(timeseries)/windowhalfwidth)*mean_coherence
gamma95 = 1.-(0.05)**(1./(edof-1.))
conf95 = np.where(cxy>gamma95)
print 'gamma95',gamma95, 'edof',edof

# Plot twin plot
fig, ax1 = plt.subplots()
# plot on ax1 the coherence
ax1.plot(fcoh, cxy, 'b-')
ax1.set_xlabel('Frequency (hr-1)')
ax1.set_ylim([0,1])
# Make the y-axis label and tick labels match the line color.
ax1.set_ylabel('Coherence', color='b')
for tl in ax1.get_yticklabels():
    tl.set_color('b')

# plot on ax2 the phase
ax2 = ax1.twinx()
ax2.plot(fcoh[conf95], phase[conf95], 'r.')
ax2.set_ylabel('Phase (degrees)', color='r')
ax2.set_ylim([-200,200])
ax2.set_yticklabels([-180,-135,-90,-45,0,45,90,135,180])

for tl in ax2.get_yticklabels():
    tl.set_color('r')

ax1.grid(True)
#ax2.grid(True)
fig.suptitle('Coherence and phase (>95%) between signal 1 and 2', fontsize='12')
plt.show()

в результате:

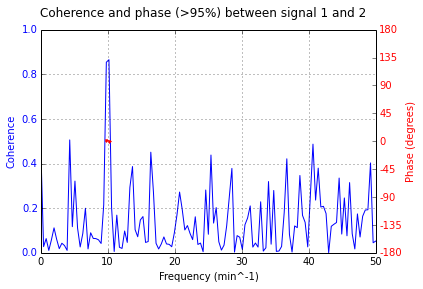
enter image description here

подводя итог: фаза самого когерентного пика составляет ~1 градус (S1 приводит s2) в течение 10 мин (при условии dt - это минутное измерения) -> (10**-1)/dt

но специалист по обработке сигналов может исправить меня, потому что я уверен на 60%, если я сделал это правильно

6

Я не уверен, где фазовая переменная была вычислена в ответе @Mattijn.

вы можете рассчитать фазовый сдвиг от угла между реальным и мнимая часть кросс-спектральной плотности.

from matplotlib import mlab

# First create power sectral densities for normalization
(ps1, f) = mlab.psd(s1, Fs=1./dt, scale_by_freq=False)
(ps2, f) = mlab.psd(s2, Fs=1./dt, scale_by_freq=False)
plt.plot(f, ps1)
plt.plot(f, ps2)

# Then calculate cross spectral density
(csd, f) = mlab.csd(s1, s2, NFFT=256, Fs=1./dt,sides='default', scale_by_freq=False)
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
# Normalize cross spectral absolute values by auto power spectral density
ax1.plot(f, np.absolute(csd)**2 / (ps1 * ps2))
ax2 = fig.add_subplot(1, 2, 2)
angle = np.angle(csd, deg=True)
angle[angle<-90] += 360
ax2.plot(f, angle)

# zoom in on frequency with maximum coherence
ax1.set_xlim(9, 11)
ax1.set_ylim(0, 1e-0)
ax1.set_title("Cross spectral density: Coherence")
ax2.set_xlim(9, 11)
ax2.set_ylim(0, 90)
ax2.set_title("Cross spectral density: Phase angle")

plt.show()

fig = plt.figure()
ax = plt.subplot(111)

ax.plot(f, np.real(csd), label='real')
ax.plot(f, np.imag(csd), label='imag')

ax.legend()
plt.show()

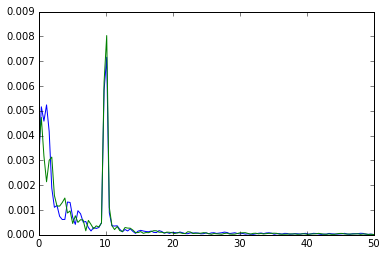
спектральная плотность мощности двух коррелируемых сигналов: The power spectral density of the two signals to be correlated

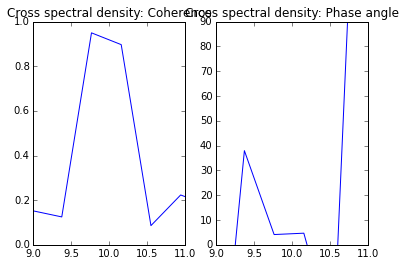
когерентность и фаза двух сигналов (увеличена до 10 Гц): The coherence and the phase of the two signals (zoomed in to 10 Hz)

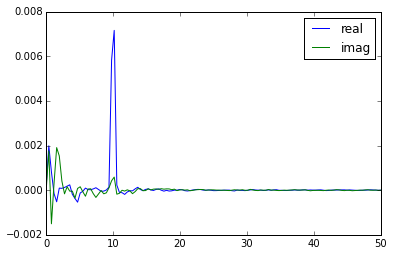
а вот реальное и мнимое(!) часть креста спектральная плотность: real and imaginary part of the cross spectral density

5

Я приготовил Jupyter Notebook что объясняет кросс-спектральный анализ, включая его неопределенности.

скриншот: enter image description here

2