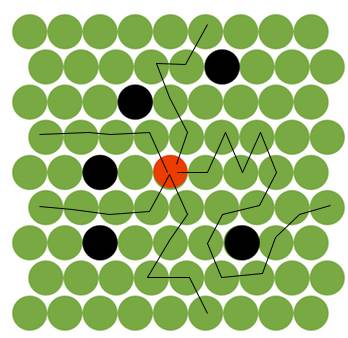
Как найти кратчайший путь в этом типе лабиринт
Red Dot - Represents the initial location
Black Dot - Already occupied
Green - Free to occupy
Destination - Boundry of the matrix [which means either x = 0 or y = 0 or x = 8 or y = 8]
на red dot может помещать себя только один ход за раз и может двигаться в одном из шести зеленых кругов, которые прикреплены к нему.
Каким будет самый быстрый метод расчета кратчайшего пути в этом типе лабиринта.
3 ответов
прежде всего, вам не нужна Dijkstra, потому что все значения ребер одинаковы. Вы можете использовать простой BFS или DFS. В худшем случае сложности одинаковы, но я бы использовал BFS, поскольку он имеет лучшую среднюю сложность случая. Тем не менее, O(|V|+|E|) - самый быстрый, который вы можете получить здесь, и это доказано.
Как представить ваш график? Лучший способ сохранить список соседей для каждого Node. Черные точки из вашего примера не учитываются как соседи. Таким образом, в вашем примере каждый узел будет иметь 0(полностью покрытый черными точками) до 6 соседей. Затем, вы можете получить в любом месте вы можете получить из любой точки узла через эти списки.
алгоритм BFS имеет свойство, которое назначает каждому узлу слой, что означает, как далеко он находится от начального узла. Вы начинаете с начальной точки, и ваш текущий слой будет равен 0. Затем вы просто следуете за всеми узлами из текущего слоя (обычно хранящегося в очереди) и пытаетесь найти его соседей(из их список соседей), которому не назначен слой, и вы назначаете им +1 более высокий слой. Как только вы найдете свой узел (который все еще может иметь X, y в качестве атрибутов для проверки границы (или границы свойства bool)), на границе вашего лабиринта, вы знаете, что это так далеко, как ваше значение слоя. Если вы хотите напечатать точный способ, вам нужно только найти путь назад (через ваши списки соседей), который соответствует условию, что каждый шаг на -1 слое ниже. Это будет печатать путь от конца до начала, но я уверен вы получите свой результат с небольшой помощью Stack структура данных :)
У вас есть "простая" проблема с графом. Связности графа является юридическим ходов. Начальный узел - это ваша красная точка. Чтобы получить один терминальный узел, придумайте еще один круг за пределами данного лабиринта; соедините все реальные выход узлов на новый круг с движением нулевой стоимости.
теперь примените алгоритм Дейкстры. Сделанный.
другой способ взглянуть на проблему с рекурсией. Переместите красную точку, отметив старое местоположение черным. Повторите с новой позиции. Возврат при выходе (длина пути возврата 1) или без законных перемещений (длина пути возврата бесконечна). Держите кратчайший известный путь.
Это поможет вам распаковать?
а* алгоритм поиска
(от: https://en.wikipedia.org/wiki/A * _search_algorithm)
следующий псевдокод описывает алгоритм[сомнительных – обсудить]:
function A*(start,goal)
ClosedSet := {} // The set of nodes already evaluated.
OpenSet := {start} // The set of tentative nodes to be evaluated, initially containing the start node
Came_From := the empty map // The map of navigated nodes.
g_score := map with default value of Infinity
g_score[start] := 0 // Cost from start along best known path.
// Estimated total cost from start to goal through y.
f_score := map with default value of Infinity
f_score[start] := g_score[start] + heuristic_cost_estimate(start, goal)
while OpenSet is not empty
current := the node in OpenSet having the lowest f_score[] value
if current = goal
return reconstruct_path(Came_From, goal)
OpenSet.Remove(current)
ClosedSet.Add(current)
for each neighbor of current
if neighbor in ClosedSet
continue // Ignore the neighbor which is already evaluated.
tentative_g_score := g_score[current] + dist_between(current,neighbor) // length of this path.
if neighbor not in OpenSet // Discover a new node
OpenSet.Add(neighbor)
else if tentative_g_score >= g_score[neighbor]
continue // This is not a better path.
// This path is the best until now. Record it!
Came_From[neighbor] := current
g_score[neighbor] := tentative_g_score
f_score[neighbor] := g_score[neighbor] + heuristic_cost_estimate(neighbor, goal)
return failure
function reconstruct_path(Came_From,current)
total_path := [current]
while current in Came_From.Keys:
current := Came_From[current]
total_path.append(current)
return total_path
Итак, насколько я понимаю , вы можете установить свой начальный узел в положение красной точки \ центральное положение, а целевой узел как x = 0 или y = 0 или x = 8 или y = 8 (вы можете сделать 4 вызова функций и взять минимум)
as для эвристических значений для узла-просто установите черные заблокированные узлы очень высокие эвристические значения, что сделает их недостижимыми, поэтому алгоритм будет проходить вокруг них.