Как найти наименьший эллипс, покрывающий заданную долю множества точек в R?

меня интересует: есть ли какая-то функция / умный способ найти маленький эллипс, охватывающий заданную долю набора 2d-точек в R? С маленький Я имею в виду эллипс наименьшей площади.

пояснение: Я в порядке с приблизительно правильным решением, если количество точек велико (как я думаю, точное решение должно было бы попробовать все комбинации подмножеств точек)

этот вопрос может звучать как дубликат вопроса эллипс, содержащий процент заданных точек в R но то, как этот вопрос сформулирован, результирующий ответ не приводит к маленький эллипс. Например, используя решение, данное эллипс, содержащий процент заданных точек в R:

require(car)
x <- runif(6)
y <- runif(6)
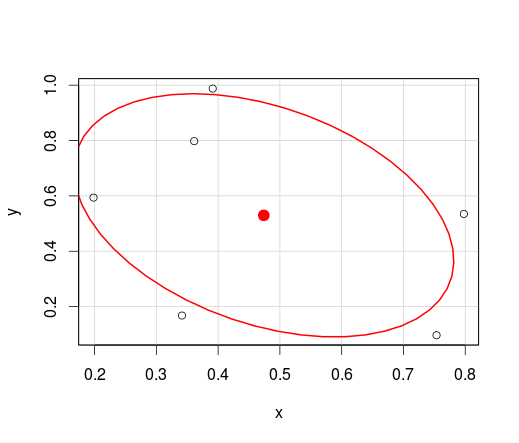
dataEllipse(x,y, levels=0.5)

полученный эллипс явно не самый маленький эллипс, содержащий половину точек, которая, я думаю, будет небольшим эллипсом закрываем три точки в левом верхнем углу.

enter image description here

6
ellipse minimum r

2 ответов

Я думаю, что у меня есть решение, которое требует двух функций cov.rob С MASS пакета и ellipsoidhull С cluster пакета. cov.rob(xy, quantile.used = 50, method = "mve") находит приблизительно "лучшие" 50 точек из общего числа 2d точек в xy которые содержатся в эллипсе минимального объема. Однако,cov.rob не возвращает напрямую этой эллипс, а скорее какой-то другой эллипс, оцененный из лучших точек (цель состоит в том, чтобы надежно оценить ковариационную матрицу). Чтобы найти подскажите минимальный эллипс, мы можем дать лучшие точки для ellipsoidhull который находит минимальный эллипс, и мы можем использовать predict.ellipse выйти координаты пути определения корпуса elllipse.

я не уверен на 100%, что этот метод является самым простым и / или что он работает на 100% (похоже, что можно избежать секундного шага использования ellipsoidhull но я не разобрался как.). Кажется, это работает на моем примере игрушки в наименьший....

хватит болтать, вот код:

library(MASS)
library(cluster)

# Using the same six points as in the question
xy <- cbind(x, y)
# Finding the 3 points in the smallest ellipse (not finding 
# the actual ellipse though...)
fit <- cov.rob(xy, quantile.used = 3, method = "mve")
# Finding the minimum volume ellipse that contains these three points
best_ellipse <- ellipsoidhull( xy[fit$best,] )
plot(xy)
# The predict() function returns a 2d matrix defining the coordinates of
# the hull of the ellipse 
lines(predict(best_ellipse), col="blue")

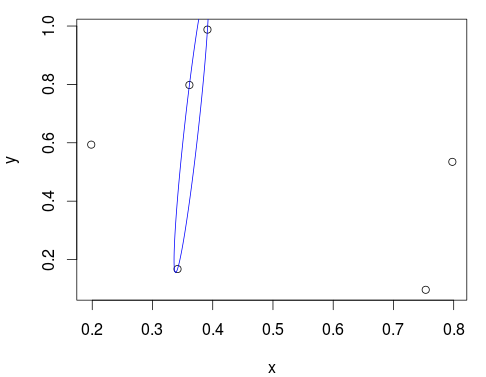
enter image description here

выглядит неплохо! Вы также можете проверить ellipse объект для получения дополнительной информации

best_ellipse
## 'ellipsoid' in 2 dimensions:
##  center = ( 0.36 0.65 ); squared ave.radius d^2 =  2 
##  and shape matrix =
##         x      y
## x 0.00042 0.0065
## y 0.00654 0.1229
##   hence, area  =  0.018

вот удобная функция, которая добавляет эллипс к существующему базовому графическому графику:

plot_min_ellipse <- function(xy, points_in_ellipse, color = "blue") {
  fit <- cov.rob(xy, quantile.used = points_in_ellipse, method = "mve")
  best_ellipse <- ellipsoidhull( xy[fit$best,] )
  lines(predict(best_ellipse), col=color)
}

давайте использовать его на большее количество точек:

x <- runif(100)
y <- runif(100)
xy <- cbind(x, y)
plot(xy)
plot_min_ellipse(xy, points_in_ellipse = 50)

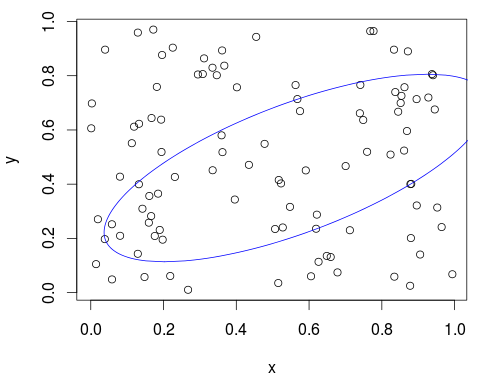
enter image description here

4

Это звучит очень похоже на доверительный интервал 2D. Попробуйте http://stat.ethz.ch/R-manual/R-devel/library/cluster/html/ellipsoidhull.html. Вероятно, вам нужно будет запустить его на каждой комбинации из N точек, а затем выбрать наименьший результат.

0