как обрабатывать асимптоту / разрыв с Matplotlib

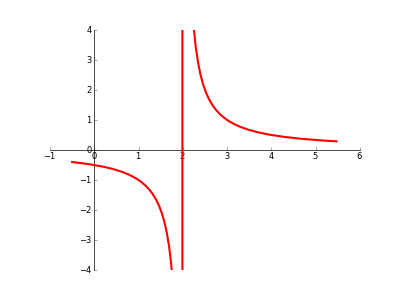
при построении графика с разрывом / асимптотой/сингулярностью / что угодно, есть ли автоматический способ предотвратить Matplotlib от "соединения точек" через "разрыв"? (см. код / изображение ниже).
Я читал, что у Sage есть средство [detect_poles], которое выглядело хорошо, но я действительно хочу, чтобы оно работало с Matplotlib.

import matplotlib.pyplot as plt 
import numpy as np
from sympy import sympify, lambdify
from sympy.abc import x

fig = plt.figure(1) 
ax = fig.add_subplot(111) 

# set up axis 
ax.spines['left'].set_position('zero') 
ax.spines['right'].set_color('none') 
ax.spines['bottom'].set_position('zero') 
ax.spines['top'].set_color('none') 
ax.xaxis.set_ticks_position('bottom') 
ax.yaxis.set_ticks_position('left') 

# setup x and y ranges and precision
xx = np.arange(-0.5,5.5,0.01) 

# draw my curve 
myfunction=sympify(1/(x-2))
mylambdifiedfunction=lambdify(x,myfunction,'numpy')
ax.plot(xx, mylambdifiedfunction(xx),zorder=100,linewidth=3,color='red') 

#set bounds 
ax.set_xbound(-1,6)
ax.set_ybound(-4,4) 

plt.show()

Discontinuity

22
equation matplotlib numpy python sympy

3 ответов

это может быть не элегантное решение, которое вы ищете, но если просто хотите получить результаты в большинстве случаев, вы можете "обрезать" большие и малые значения ваших построенных данных в +∞ и -∞ соответственно. Библиотек matplotlib не сюжет эти. Конечно, вы должны быть осторожны, чтобы не сделать ваше разрешение слишком низким или порог отсечения слишком высоким.

utol = 100.
ltol = -100.
yy = 1/(xx-2)
yy[yy>utol] = np.inf
yy[yy<ltol] = -np.inf

ax.plot(xx, yy, zorder=100, linewidth=3, color='red')
13

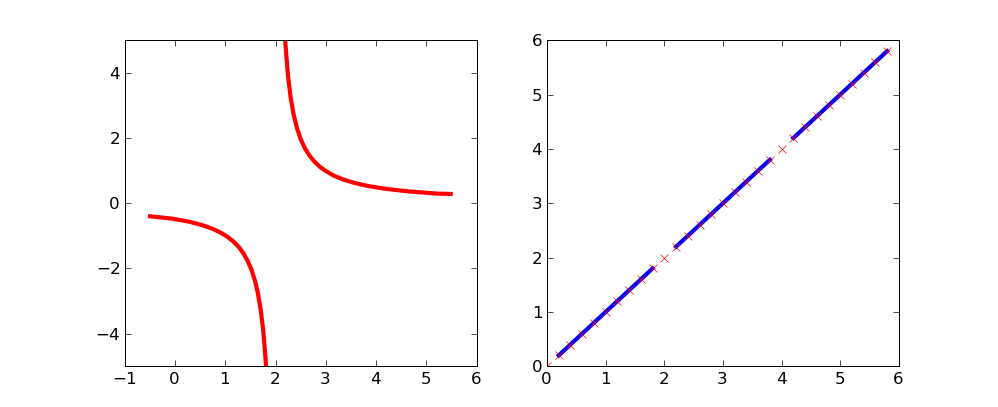
С помощью массивы в масках вы можете избежать построения выбранных областей кривой.

удалить сингулярность при x=2:

import matplotlib.numerix.ma as M    # for older versions, prior to .98
#import numpy.ma as M                # for newer versions of matplotlib
from pylab import *

figure()

xx = np.arange(-0.5,5.5,0.01) 
vals = 1/(xx-2)        
vals = M.array(vals)
mvals = M.masked_where(xx==2, vals)

subplot(121)
plot(xx, mvals, linewidth=3, color='red') 
xlim(-1,6)
ylim(-5,5)

эта простая кривая может быть немного более ясной, на которой точки исключены:

xx = np.arange(0,6,.2) 
vals = M.array(xx)
mvals = M.masked_where(vals%2==0, vals)
subplot(122)
plot(xx, mvals, color='b', linewidth=3)
plot(xx, vals, 'rx')
show()

enter image description here

21

Нет, я думаю, что нет встроенного способа сказать matplotlib игнорировать эти точки. В конце концов, он просто соединяет точки и ничего не знает о функциях или что происходит между точками.

однако, вы можете использовать sympy чтобы найти полюса, а затем соединить непрерывные части вашей функции вместе. Вот какой-то, по общему признанию, уродливый код, который делает именно это:

from pylab import *
from sympy import solve
from sympy.abc import x
from sympy.functions.elementary.complexes import im

xmin = -0.5
xmax = 5.5
xstep = 0.01

# solve for 1/f(x)=0 -- we will have poles there
discontinuities = sort(solve(1/(1/(x-2)),x))

# pieces from xmin to last discontinuity
last_b = xmin
for b in discontinuities:
    # check that this discontinuity is inside our range, also make sure it's real
    if b<last_b or b>xmax or im(b):
      continue
    xi = np.arange(last_b, b, xstep)
    plot(xi, 1./(xi-2),'r-')
    last_b = b

# from last discontinuity to xmax
xi = np.arange(last_b, xmax, xstep)
plot(xi, 1./(xi-2),'r-')

xlim(xmin, xmax)
ylim(-4,4)
show()

пример http://i43.tinypic.com/30mvbzb.jpg

5