Как определить, пересекает ли эллипс (сталкивается с) кругом

эллипс определяется набором точек, сумма расстояния до точки A и расстояния до точки B постоянна e. (A и B называются фокусами эллипса).

все точки P, сумма AP + BP которых меньше e, лежат внутри эллипса.

круг определяется как множество точек, расстояние до точки C равно r.

простой тест на пересечение круга и эллипса следующий:

найти
P как пересечение круг и линия AC и
Q как пересечение окружности и линии BC.

круг и Эллипс пересекаются (или круг лежит полностью внутри эллипса), если
AP + BP

редактировать:

после комментария Мартина Демелло и адаптации моего ответа соответственно я подумал больше о проблеме и обнаружил, что ответ (со 2-й проверкой) все еще не обнаруживает все перекрестках:

Если круг и Эллипс пересекаются только очень редко (только немного больше, чем касательная) P и Q не будут лежать внутри эллипса:

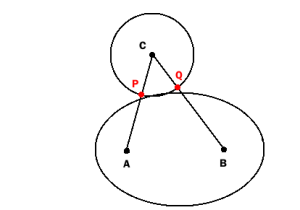
таким образом, описанный выше тест обнаруживает столкновение только в том случае, если перекрытие "достаточно большое". Возможно, это достаточно хорошо для ваших практических целей, хотя математически это не идеально.

увеличьте большой и малый радиусы эллипса на радиус окружности. Затем проверьте, находится ли центр данной окружности внутри этого нового большего эллипса, суммируя расстояния до фокусов увеличенного эллипса.

этот алгоритм довольно эффективен. Вы можете рано выйти, если данный круг не пересекает круг, который описывает эллипс. Это медленнее, чем тест с ограничительной рамкой, но найти ограничительную рамку не выровненного по оси эллипса сложно.

найдите точку на эллипсе, ближайшую к центру круга
а затем проверьте, меньше ли расстояние от этой точки радиуса окружности
если вам нужна помощь в этом, просто прокомментируйте, но это просто исчисление

edit: вот пути к решению, так как есть что-то не так с творогом

заданный центр α β на эллипсе
и (из-за отсутствия запоминания термина) радиус x A, радиус y b этот параметризация
Р(Θ) = (АВ)/( ( (BcosΘ)^2 + (asinΘ)^2 )^.5)
x(Θ) = α + sin(Θ)r (Θ)
y(Θ) = β + cos(Θ)r (Θ)

а затем просто возьмите круг с центром в (φ, ψ) и радиусом r тогда расстояние d (Θ) = ((φ - x (Θ))^2 + (ψ - y (Θ) )^2)^.5

минимум этого расстояния, когда d ' (Θ) = 0 ('для производной)

д'(Θ) = 1/Д(Θ) * (-φx'(Θ) + х(Θ)х'(Θ) - ψy'(Θ) + г(Θ)г'(Θ) )
==>
x'(Θ) * (- φ + x (Θ)) = y ' (Θ) * (ψ - y (Θ))

и продолжайте идти и идти, и, надеюсь, вы можете решить для Θ
Рамки, в которых вы работаете, могут помочь вам решить эту проблему, и вы всегда можете найти простой выход и приблизительные корни через метод Ньютона

если круг и Эллипс сталкиваются, то либо их границы пересекаются 1, 2, 3 или 4 раза(или бесконечно много в случае кругового эллипса, совпадающего с кругом), либо круг находится внутри эллипса или наоборот.

Я предполагаю, что круг имеет уравнение (x-a)^2 + (y - b)^2

чтобы проверить, находится ли один из них внутри другого, вы можете оцените уравнение окружности по координатам центра эллипса (x=c, y=e) или наоборот и посмотрите, выполняется ли неравенство.

чтобы проверить другие случаи, в которых их границы пересекаются, вы должны проверить, имеет ли система уравнений, описанная (1) и (2), какие-либо решения.

вы можете сделать это, добавив (1) и (2), давая вам

(x - a)^2 + (y - b)^2 + [(x - c)^2]/[d^2] + [(y - e)^2]/[f^2] = r^2 + 1

далее вы умножаете условия, давая

x^2 - 2ax + a^2 + y^2 - 2by + b^2 + x^2/d^2 - 2cx/d^2 + c^2/d^2 + y^2/f^2 - 2ey/f^2 + e^2/f^2 = r^2 + 1

собирая как термины, мы получаем

(1 + 1/d^2)x^2 - (2a + 2c/d^2)x + (1 + 1/f^2)y^2 - (2b + 2e/f^2)y = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

теперь m = (1 + 1/d^2), n = -(2a + 2c/d^2), o = (1 + 1/f^2), and p = -(2b + 2e/f^2)

уравнение теперь mx^2 + nx + oy^2 + py = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

теперь нам нужно заполнить квадраты на левой стороне

m[x^2 + (n/m)x] + o[y^2 + (p/o)y] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m[x^2 + (n/m)x + (n/2m)^2 - (n/2m)^2] + o[y^2 + (p/o)y + (p/2o)^2 - (p/2o)^2] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m[(x + n/2m)^2 - (n/2m)^2] + o[(y + p/2o)^2 - (p/2o)^2] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m(x + n/2m)^2 - m(n/2m)^2 + o(y + p/2o)^2 - o(p/2o)^2 = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m(x + n/2m)^2 + o(y + p/2o)^2 = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2 + m(n/2m)^2 + o(p/2o)^2

эта система имеет решение iff 11 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2 + m(n/2m)^2 + o(p/2o)^2 >= 0

вот оно что, если бы я не сделал никаких алгебраических ошибок. Я не знаю, насколько вы можете упростить полученное выражение, поэтому это решение может быть довольно вычислительно дорого, если вы собираетесь проверить много кругов / эллипсов

забудьте о математическом решении. Как вы можете легко видеть на рисунке, у вас может быть до четырех решений, и, следовательно, вероятно, полином четвертого класса.

вместо этого просто выполните двоичный поиск по краю одной из фигур. Легко определить, находится ли точка внутри эллипса и тем более в окружности (просто посмотрите, меньше ли расстояние, чем радиус).

Если вы действительно хотите пойти на математику, Wolfram MathWorld имеет хорошую статью здесь: http://mathworld.wolfram.com/Circle-EllipseIntersection.html но будьте осторожны, вам все равно придется написать решатель полиномиальных уравнений, возможно, используя что-то вроде двоичного поиска.

Это не так сложно. ответ user168715 обычно правильный, но делать исчисление не обязательно. Только тригонометрия.

найдите угол между центром двух объектов. Используя это, вы можете найти ближайшую точку к центру круга на эллипсе, используя полярную форму:

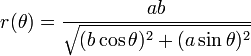
(взято из статьи Википедии о эллипсы)

теперь сравните расстояние между двумя центрами объекта, вычитая радиус эллипса и радиус окружности.

может быть, я что-то упускаю; может быть, ArcTan/Cos/Sin медленны, но я так не думаю, и при необходимости должны быть быстрые приближения.

Я знаю, что уже слишком поздно, но я надеюсь, что это поможет кому-то. Мой подход к решению этой проблемы состоял в том, чтобы интерполировать эллипс в многоугольник n-измерений, затем построить линию между каждые 2 точками и найти, пересекается ли круг с какой-либо из линий или нет. Это не обеспечивает наилучшую производительность, но это удобно и легко реализовать.

для интерполяции эллипса в n-мерный многоугольник можно использовать:

    float delta = (2 * PI) / n;

    std::vector<Point*> interpolation;

    for(float t = 0; t < (2 * PI); t += delta) {

        float x = rx * cos(t) + c->get_x();
        float y = ry * sin(t) + c->get_y();

        interpolation.push_back(new Point(x, y));
    }

c: центр эллипс. rx: радиус X-выровненной оси эллипса. ry: радиус y-выровненной оси эллипса.

теперь у нас есть точки интерполяции, мы можем найти пересечение между окружностью и линиями между каждые 2 точками. Описан один из способов найти пересечение линии-крикля здесь, пересечение происходит, если пересечение произошло между любой из линий и окружности.

надеюсь, это кому-нибудь поможет.

предположим,: эллипс центрируется в начале координат и с полу-мажором ось (длины a), ориентированная вдоль оси x, и с полу-минором ось длины b; E2-эксцентриситет в квадрате, то есть (aa-bb)/(a*a); окружность центрирована на X, Y и радиуса r.

легкие случаи: центр круга находится внутри эллипса (т. е. гипотеза (X/a, Y/b) a+r), поэтому пересечения нет.

один подход для других случаев заключается в вычислении геодезического координаты (широта, высота) центра круга. Круг пересекает эллипс тогда и только тогда, когда высота меньше радиуса.

геодезическая широта точки на эллипсе - это угол нормаль к эллипсу в точке с осью X, и высота точки вне эллипса расстояние точки с точки на ближайшем к нему эллипсе. Обратите внимание на геодезические широта не совпадает с полярным углом от центра эллипса до точки, если эллипс на самом деле круговой.

в формулах преобразование из геодезических координат lat, ht в декартовые координаты X, Y X = (nu+ht) * cos( lat), Y = (nu * (1-E2) + ht)*sin (lat) где nu = a / sqrt(1 - E2*sin (lat)sin (lat)). Точка на эллипсе, ближайшая к X, Y-точка с той же широтой, но нулевой высотой, т. е. x = нуcos(lat), y = nu * (1-E2) * sin (lat). Обратите внимание, что nu является функцией широты.

к сожалению, процесс поиска lat, ht из X, Y является итерационный один. Один из подходов заключается в том, чтобы сначала найти широту, а затем высота.

небольшая алгебра показывает, что широта удовлетворяет широта = инструмент atan2( г+ Е2*нюsin (lat), X) который может быть использован для вычисления последовательных приближений к широте, начиная с lat = atan2( Y, X(1.0-E2)), или (более эффективно) может быть решается с использованием метода Ньютона.

большой Е2, т. е. льстить эллипса, тем больше потребуются итерации. Например, если эллипс почти круговой (скажем, E2

наконец, учитывая широту, высота может быть вычислена путем вычисления (x, y): x = nucos( lat), y = ну(1-E2)*sin (lat) и тогда h-расстояние от x, y до центра круга, h = hypot (X-x, Y-y)

Я хотел бы внести некоторый вклад в более общую проблему, связанную с контактом между двумя эллипсами. Расчет расстояния наибольшего сближения двух эллипсов была давняя проблема и была решена аналитически только в течение последних десяти лет-это отнюдь не просто. Решение проблемы можно найти здесь http://www.e-lc.org/docs/2007_01_17_00_46_52/.

общий метод, чтобы определить, есть ли контакт между двумя эллипсами сначала вычислите расстояние ближайшего приближения эллипсов в их текущей конфигурации, а затем вычитайте это из их текущей величины разделения. Если этот результат меньше или равен 0, то они находятся в Контакте.

Если кто-то заинтересован, я могу опубликовать код, который вычисляет расстояние ближайшего подхода-это в C++. Код предназначен для общего случая двух произвольных эллипсов, но вы, очевидно, можете сделать это для круга и эллипса, так как круг является эллипсом с равные малые и большие оси.