Как оптимизировать вложенный цикл for в Python
поэтому я пытаюсь написать функцию python для возврата метрики, называемой значением R Mielke-Berry. Метрика вычисляется как так:
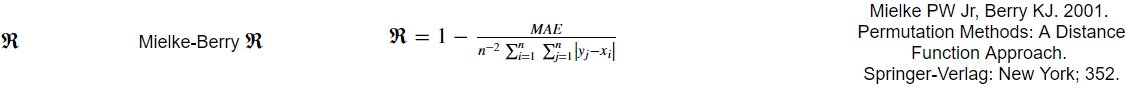
текущий код, который я написал, работает, но из-за суммы сумм в уравнении единственное, что я мог придумать, чтобы решить его, это использовать вложенный цикл for в Python, который очень медленный...
Ниже приведен мой код:
def mb_r(forecasted_array, observed_array):
"""Returns the Mielke-Berry R value."""
assert len(observed_array) == len(forecasted_array)
y = forecasted_array.tolist()
x = observed_array.tolist()
total = 0
for i in range(len(y)):
for j in range(len(y)):
total = total + abs(y[j] - x[i])
total = np.array([total])
return 1 - (mae(forecasted_array, observed_array) * forecasted_array.size ** 2 / total[0])
почему я преобразовал входных массивов в списки, потому что я слышали (еще не протестировали), что индексирование массива numpy с использованием цикла python for очень медленное.
Я чувствую, что может быть какая-то функция numpy, чтобы решить это намного быстрее, кто-нибудь знает что-нибудь?
3 ответов
вещание в numpy
если вы не ограничены памятью, первый шаг для оптимизации вложенных циклов в numpy использовать широковещание и выполнять операции векторизованным способом:
import numpy as np
def mb_r(forecasted_array, observed_array):
"""Returns the Mielke-Berry R value."""
assert len(observed_array) == len(forecasted_array)
total = np.abs(forecasted_array[:, np.newaxis] - observed_array).sum() # Broadcasting
return 1 - (mae(forecasted_array, observed_array) * forecasted_array.size ** 2 / total[0])
но в то время как в этом случае цикл происходит в C вместо Python, он включает в себя выделение массива size (N, N).
трансляция не панацея, попробуйте развернуть внутренний цикл
как было отмечено выше, вещание подразумевает огромное память. Поэтому его следует использовать с осторожностью и не всегда правильный путь. Хотя у вас может быть первое впечатление, чтобы использовать его везде - не. Не так давно я тоже был смущен этим фактом, см. мой вопрос Numpy ufuncs скорость vs для скорости петли. Чтобы не быть слишком многословным, я покажу это на вашем примере:
import numpy as np
# Broadcast version
def mb_r_bcast(forecasted_array, observed_array):
return np.abs(forecasted_array[:, np.newaxis] - observed_array).sum()
# Inner loop unrolled version
def mb_r_unroll(forecasted_array, observed_array):
size = len(observed_array)
total = 0.
for i in range(size): # There is only one loop
total += np.abs(forecasted_array - observed_array[i]).sum()
return total
небольшие массивы (вещание быстрее)
forecasted = np.random.rand(100)
observed = np.random.rand(100)
%timeit mb_r_bcast(forecasted, observed)
57.5 µs ± 359 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
%timeit mb_r_unroll(forecasted, observed)
1.17 ms ± 2.53 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
массивы среднего размера (равные)
forecasted = np.random.rand(1000)
observed = np.random.rand(1000)
%timeit mb_r_bcast(forecasted, observed)
15.6 ms ± 208 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%timeit mb_r_unroll(forecasted, observed)
16.4 ms ± 13.3 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
массивы большого размера (вещание медленнее)
forecasted = np.random.rand(10000)
observed = np.random.rand(10000)
%timeit mb_r_bcast(forecasted, observed)
1.51 s ± 18 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
%timeit mb_r_unroll(forecasted, observed)
377 ms ± 994 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
как вы можете видеть для небольших массивов транслировать версия 20x быстрее, чем развернутый, для средних массивов они , а равны, но для массивов больших размеров это 4X медленнее потому что память накладные расходы сами по себе дорого обходятся.
Numba jit и распараллеливание
другой подход-использовать numba и магия мощный
вот один векторизованный способ использоватьbroadcasting и total -
np.abs(forecasted_array[:,None] - observed_array).sum()
чтобы принять как списки, так и массивы, мы можем использовать numpy builtin для внешнего вычитания, например -
np.abs(np.subtract.outer(forecasted_array, observed_array)).sum()
мы также можем использовать numexpr модуль быстрее absolute вычисления и выполнение summation-reductions в одном numexpr evaluate вызов и как таковой будет гораздо более эффективной памятью, например -
import numexpr as ne
forecasted_array2D = forecasted_array[:,None]
total = ne.evaluate('sum(abs(forecasted_array2D - observed_array))')
в качестве примера, следующий код:
#pythran export mb_r(float64[], float64[])
import numpy as np
def mb_r(forecasted_array, observed_array):
return np.abs(forecasted_array[:,None] - observed_array).sum()
работает на следующей скорости на чистом CPython:
% python -m perf timeit -s 'import numpy as np; x = np.random.rand(400); y = np.random.rand(400); from mbr import mb_r' 'mb_r(x, y)'
.....................
Mean +- std dev: 730 us +- 35 us
и при компиляции с Pythran Я
% pythran -march=native -DUSE_BOOST_SIMD mbr.py
% python -m perf timeit -s 'import numpy as np; x = np.random.rand(400); y = np.random.rand(400); from mbr import mb_r' 'mb_r(x, y)'
.....................
Mean +- std dev: 65.8 us +- 1.7 us
так примерно X10 ускорение, на одном ядре с расширением AVX.
