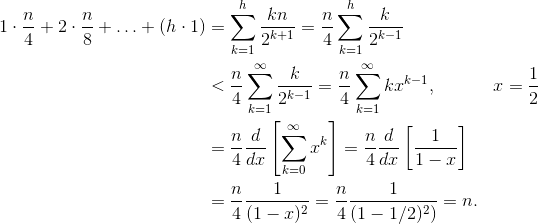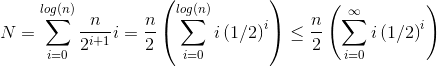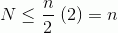Как построение кучи может быть o (n) временной сложностью?
может кто-нибудь помочь объяснить, как можно построить кучу o(n) сложности?
вставка элемента в кучу составляет O(log n), и вставка повторяется n / 2 раза (остальные-листья и не могут нарушать свойство кучи). Итак, это означает, что сложность должна быть O(n log n), Я думаю.
другими словами, для каждого элемента, который мы "нагромождаем", у него есть потенциал, чтобы отфильтровать один раз для каждого уровня для кучи до сих пор (который является log n уровни.)
что я упустил?
14 ответов
я думаю, что в этой теме есть несколько вопросов:
- как вы реализуете buildHeap, чтобы он работал в O (n) времени?
- как вы показываете, что buildHeap работает в O (n) время при правильной реализации?
- почему эта же логика не работает, чтобы выполнить сортировку кучи в O (n) времени, а не O (N log n)?
часто, ответы на эти вопросы внимания о разнице между siftUp и siftDown. Правильный выбор между siftUp и siftDown важно получить O (n) производительность buildHeap, но ничего не делает, чтобы помочь понять разницу между buildHeap и heapSort в целом. Действительно, правильные реализации обоих buildHeap и heapSort будет только использовать siftDown. The siftUp операция необходима только для выполнения вставок в существующую кучу, поэтому она будет использоваться для реализации приоритета например, очередь с использованием двоичной кучи.
я написал это, чтобы описать, как максимум куча работы. Это тип кучи, обычно используемый для сортировки кучи или для очереди приоритетов, где более высокие значения указывают на более высокий приоритет. Также полезна минимальная куча; например, при получении элементов с целочисленными ключами в порядке возрастания или строк в алфавитном порядке. Принципы точно такие же, просто изменить порядок сортировки.
на куча собственность указывает, что каждый узел в двоичной куче должен быть по крайней мере таким же большим, как оба его дочерних узла. В частности, это означает, что самый большой элемент в куче находится в корне. Просеивание вниз и просеивание вверх-это, по сути, одна и та же операция в противоположных направлениях: переместить узел-нарушитель, пока он не удовлетворит свойству кучи:
-
siftDownменяет местами слишком маленький узел с его самым большим дочерним узлом (тем самым перемещая его вниз), пока он не станет по крайней мере таким же большим, как оба узла ниже него. -
siftUpобменивает узел, который слишком велик с его родителем (тем самым перемещая его вверх), пока он не будет не больше, чем узел над ним.
количество операций, необходимых для siftDown и siftUp пропорциональна расстоянию узел мог двигаться. Для siftDown, это расстояние от нижней части дерева, так siftDown дорого для узлов в верхней части дерева. С siftUp, работа пропорциональна расстоянию от вершины дерева, поэтому siftUp дорого для узлов в нижней части дерева. Хотя обе операции O (log n) в худшем случае в куче только один узел находится вверху, тогда как половина узлов лежит в нижнем слое. Так что не должно быть слишком удивительно, что если мы должны применить операцию к каждому узлу, мы предпочли бы siftDown над siftUp.
на buildHeap функция принимает массив несортированных элементов и перемещает их, пока все они не удовлетворяют свойству кучи, таким образом, создается допустимая куча. Есть два подхода, которые можно принять за buildHeap С помощью siftUp и siftDown операции, которые мы описали.
начните с верхней части кучи (начало массива) и вызовите
siftUpпо каждому пункту. На каждом шаге ранее просеянные элементы (элементы перед текущим элементом в массиве) образуют допустимую кучу, и просеивание следующего элемента помещает его в допустимую позицию в куче. После просеивания каждого узла все элементы удовлетворяют свойству кучи.или идите в противоположном направлении: начните с конца массива и двигайтесь назад к фронту. На каждой итерации вы просеиваете элемент вниз, пока он не окажется в правильном месте.
оба этих решения создадут допустимую кучу. Вопрос в том, какая реализация для buildHeap эффективнее? Неудивительно, что это вторая операция, которая использует siftDown.
давайте h = log n определить высоту кучи. Работа, необходимая для siftDown подход задается суммой
(0 * n/2) + (1 * n/4) + (2 * n/8) + ... + (h * 1).
каждый член в сумме имеет максимальное расстояние, которое узел на данной высоте должен будет переместить (ноль для нижнего слоя, h для корня), умноженное на количество узлов на этой высоте. Напротив, сумма для вызова siftUp на каждый узел
(h * n/2) + ((h-1) * n/4) + ((h-2)*n/8) + ... + (0 * 1).
это должно быть ясно, что вторая сумма больше. Только первый срок is hn / 2 = 1/2 N log n, так что этот подход имеет сложность в лучшем случае O (N log n). Но как мы докажем, что сумма siftDown подход действительно O (n)? Один из методов (есть и другие анализы, которые также работают) - превратить конечную сумму в бесконечный ряд, а затем использовать ряд Тейлора. Мы можем игнорировать первый член, который равен нулю:
если вы не уверены, почему каждый из этих шагов работает, вот обоснование процесса в словах:
- все члены положительны, поэтому конечная сумма должна быть меньше бесконечной суммы.
- серия равна серии мощности, оцениваемой в x=1/2.
- этот степенной ряд равен (постоянное время) производной ряда Тейлора для f(x)=1/(1-x).
- x=1/2 находится в интервале сходимости этого Тейлора серии.
- таким образом, мы можем заменить ряд Тейлора с 1/(1-x), дифференцировать и оценивать, чтобы найти значение бесконечного ряда.
так как бесконечная сумма точно n, мы заключаем, что конечная сумма не больше и, следовательно,O (n).
следующий вопрос: если можно запустить buildHeap в линейное время, почему сортировка кучи требует O (N log n) времени? Ну, сортировка кучи состоит из двух этапов. Во-первых, мы называем buildHeap на массиве, который требует O (n) время, если реализован оптимально. Следующий этап-повторно удалить самый большой элемент в куче и поместить его в конец массива. Поскольку мы удаляем элемент из кучи, всегда есть открытое место сразу после конца кучи, где мы можем сохранить элемент. Таким образом, сортировка кучи достигает отсортированного порядка, последовательно удаляя следующий по величине элемент и помещая его в массив начиная с последней позиции и двигаться вперед. Именно сложность этой последней части доминирует в сортировке кучи. Петля выглядит так:
for (i = n - 1; i > 0; i--) {
arr[i] = deleteMax();
}
ясно, что цикл выполняется O (n) раз (n-1 если быть точным, последний пункт уже на месте). Сложность deleteMax для кучи O (log n). Обычно он реализуется путем удаления корня (самого большого элемента, оставшегося в куче) и замены его последним элементом в куче, который является листом, и, следовательно, одним из самых маленьких предметов. Этот новый корень почти наверняка нарушит свойство кучи, поэтому вам нужно вызвать siftDown пока вы не переместите его обратно в приемлемом положении. Это также имеет эффект перемещения следующего по величине элемента до корня. Обратите внимание, что, в отличие от buildHeap где для большинства узлов мы называем siftDown из нижней части дерева, мы назвали siftDown С вершины дерева на каждой итерации! хотя дерево сокращаясь, он не сжимается достаточно быстро: высота дерева остается постоянной, пока вы не удалите первую половину узлов (когда вы полностью очистите нижний слой). Тогда для следующей четверти высота h-1. Таким образом, общая работа для этого второго этапа
h*n/2 + (h-1)*n/4 + ... + 0 * 1.
обратите внимание на переключатель: теперь нулевой рабочий случай соответствует одному узлу и h рабочий случай соответствует половине узлов. Эта сумма O (N log n) как неэффективные версии buildHeap это реализовано с помощью siftUp. Но в этом случае у нас нет выбора, так как мы пытаемся сортировать, и мы требуем, чтобы следующий по величине элемент был удален следующим.
в общем, работа для сортировки кучи-это сумма двух этапов:O (n) время для buildHeap и о(n записей N), чтобы удалить каждый узел в порядке, поэтому сложность O (N log n). Вы можете доказать (используя некоторые идеи из теории информации), что для сортировка на основе сравнения,O (N log n) это лучшее, на что вы могли бы надеяться в любом случае, поэтому нет причин разочаровываться в этом или ожидать, что сортировка кучи достигнет o(n) привязки по времени, что buildHeap делает.
ваш анализ правильный. Однако, это не туго.
не очень легко объяснить, почему построение кучи является линейной операцией, вам лучше ее прочитать.
A большой анализ алгоритма можно увидеть здесь.
основная идея заключается в том, что в фактический heapify стоимость не O(log n)для всех элементов.
, когда heapify вызывается, время выполнения зависит о том, как далеко элемент может переместиться в дереве до завершения процесса. Другими словами, это зависит от высоты элемента в кучу. В худшем случае элемент может опуститься до уровня листа.
давайте считать работу на уровне.
на самом нижнем уровне есть 2^(h)узлы, но мы не называем heapify на любой из них, поэтому работа равна 0. На следующем уровне есть 2^(h − 1) узлы, и каждый может двигаться вниз на 1 уровень. На 3-м уровне снизу, есть 2^(h − 2) узлы, и каждый может двигаться вниз на 2 уровнях.
как вы можете видеть, не все операции heapify являются O(log n), вот почему вы получаете O(n).
интуитивно:
"сложность должна быть O (nLog n)... для каждого элемента мы "нагромождаем", у него есть потенциал, чтобы отфильтровать один раз для каждого уровня для кучи до сих пор (который является уровнем журнала n)."
не совсем. Ваша логика не создает жесткой границы - она оценивает сложность каждой кучи. Если построено снизу вверх, вставка (heapify) может быть намного меньше, чем O(log(n)). Процесс как следует:
( Шаг 1 ) первый n/2 элементы идут в нижней строке кучи. h=0, поэтому heapify не требуется.
( Шаг 2 ) следующий n/22 элементы идут в строке 1 снизу вверх. h=1, heapify фильтры 1 уровень вниз.
( пункт я )
следующий n/2i элементы идут в строку i снизу вверх. h=i, heapify filters i уровни вниз.
( пункт log (n) ) последние n/2log2(n) = 1 элемент идет в строку log(n) снизу вверх. h=log(n), heapify filters log(n) уровни вниз.
обратите внимание: что после первого шага,1/2 элементов (n/2) уже в куче, и нам даже не нужно было вызывать heapify один раз. Кроме того, обратите внимание, что только один элемент, корень, фактически вызывает полный log(n) сложности.
теоретически:
общее количество шагов N построить кучу размере n, можно записать математически.
на высоте i, мы показали (выше), что будет n/2i+1 элементы, которые нужно вызвать heapify, и мы знаем heapify на высоте i is O(i). Это дает:
решение последнего суммирования можно найти с помощью принимая производную от обеих сторон известного уравнения геометрического ряда:
и, наконец, вставляю x = 1/2 в приведенное выше уравнение дает 2. Включение этого в первое уравнение дает:
таким образом, общее количество шагов имеет размер O(n)
Это будет O (N log n), если вы построили кучу, повторно вставляя элементы. Однако вы можете создать новую кучу более эффективно, вставив элементы в произвольном порядке, а затем применив алгоритм для "нагромождения" их в надлежащем порядке (в зависимости от типа кучи, конечно).
см.http://en.wikipedia.org/wiki/Binary_heap," построение кучи " для примера. В этом случае вы по существу работаете вверх от нижнего уровня дерева, меняя местами родительские и дочерние узлы, пока не будут выполнены условия кучи.
при создании кучи, скажем, вы принимаете подход снизу вверх.
- вы берете каждый элемент и сравниваете его с его дочерними элементами, чтобы проверить, соответствует ли пара правилам кучи. Таким образом, поэтому листья попадают в кучу бесплатно. Это потому, что у них нет детей.
- двигаясь вверх, худший сценарий для узла прямо над листьями будет 1 сравнение (при максимальном они будут сравниваться только с одним поколением дети)
- двигаясь дальше, их непосредственные родители могут быть сопоставлены с двумя поколениями детей.
- продолжая в том же направлении, вы будете иметь log(n) сравнения для корня в худшем случае. и log(n)-1 для его ближайших детей, log (n)-2 для их ближайших детей и так далее.
Как мы знаем, высота кучи log (n), где n-общее количество элементов.Давайте представим его как h
Когда мы выполняем операцию heapify, то элементы на последнем уровне (h) не будет двигаться ни на шаг.
количество элементов на втором последнем уровне (h-1) is 2h-1 и они могут двигаться на max 1 уровень (во время heapify).
аналогично, для Яth, S=n + log (n)
T(C)=O (n)
в случае построения кучи, мы начинаем с высоты, logn -1 (где logn-высота дерева из n элементов). Для каждого элемента, присутствующего на высоте "h", мы идем на максимальной высоте вверх (logn-h) вниз.
So total number of traversal would be:-
T(n) = sigma((2^(logn-h))*h) where h varies from 1 to logn
T(n) = n((1/2)+(2/4)+(3/8)+.....+(logn/(2^logn)))
T(n) = n*(sigma(x/(2^x))) where x varies from 1 to logn
and according to the [sources][1]
function in the bracket approaches to 2 at infinity.
Hence T(n) ~ O(n)
последовательные вставки могут быть описаны:
T = O(log(1) + log(2) + .. + log(n)) = O(log(n!))
по приближению Старлинга,n! =~ O(n^(n + O(1))), поэтому T =~ O(nlog(n))
надеюсь, это поможет, оптимальный способ O(n) использует алгоритм сборки кучи для данного набора (порядок не имеет значения).
@bcorso уже продемонстрировал доказательство анализа сложности. Но ради тех, кто все еще изучает анализ сложности, я должен добавить следующее:
основа вашей первоначальной ошибки связана с неправильным истолкованием значения утверждения "вставка в кучу занимает O (log n) время". Вставка в кучу действительно O (log n), но вы должны признать, что n-это размер кучи при вставке.
в контексте при вставке n объектов в кучу сложность I-й вставки равна O (log n_i), где n_i-размер кучи, как при вставке i. Только последняя вставка имеет сложность O (log n).
Мне очень нравится объяснение Джереми Уэст.... другой подход, который действительно легко понять, приведен здесь http://courses.washington.edu/css343/zander/NotesProbs/heapcomplexity
поскольку, buildheap зависит от использования, зависит от heapify и используется подход shiftdown, который зависит от суммы высот всех узлов. Итак, чтобы найти сумму высоты узлов, которая задается S = суммирование от i = 0 до i = h из (2^i*(h-i)), где h = logn высота дерева решая s, получаем s = 2^(h+1) - 1 - (h+1) так как, n = 2^(h+1) - 1 s = n-h-1 = N-logn-1 s = O(n), и поэтому сложность buildheap равна O (n).
"линейная временная граница кучи сборки может быть показана путем вычисления суммы высот всех узлов в куче, которая является максимальным числом пунктирных линий. Для идеального бинарного дерева высоты h, содержащего N = 2^(h+1) – 1 узлов, сумма высот узлов равна N – H – 1. Таким образом, Это O(N)."
в основном, работа выполняется только на не-листовых узлах при построении кучи...и проделанная работа-это количество подкачки вниз для удовлетворения условия кучи...другими словами (в худшем случае) количество пропорционально высоте узла...в целом сложность задачи пропорциональна сумме высот всех не-листовых узлов..то есть (2^h+1-1)-h-1=n-h-1= O(n)
доказательство не фантазии, и довольно просто, я только доказал случай для полного двоичного дерева, результат может быть обобщен для полного двоичного дерева.
думаю, вы делаете ошибку. Взгляните на это:http://golang.org/pkg/container/heap/ построение кучи isn'y O (n). Однако вставка-O(lg (n). Я предполагаю, что инициализация O (n) если вы задаете размер кучи b/c, куча должна выделить пространство и настроить структуру данных. Если у вас есть n элементов, чтобы положить в кучу, то да, каждая вставка lg(n) и есть n элементов, поэтому вы получаете N*lg (n), как указано