Как построить линию (полигональную цепь) с numpy/scipy / matplotlib с минимальным сглаживанием

Я пытаюсь построить линию в matplotlib.. Я ищу правильный тип интерполяции.. Я хочу что-то вроде этого!--3-->

taken from canvasxpress.org/line.html

где каждая линия разглаживается. Я попробовал несколько комбинаций scipy и matplotlib, таких как

x_new = np.arange(x, x_length, 1)
tck = interpolate.splrep(x, y, s=3)
y_new = interpolate.splev(x_new, tck, der=0)
ax.plot(x_new, y_new, color+lstyle)

но лучший результат я получаю

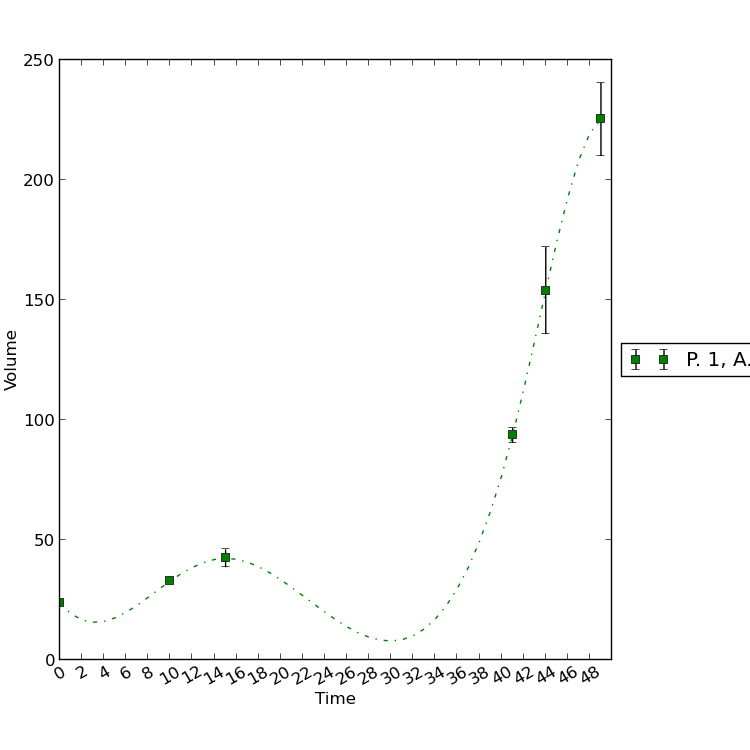
my result

строка представляет увеличение переменной.. так что это неправильное представление. Что мне искать? для?

спасибо

Edit: я думаю о реализации метода от себя, но я не знаю, было ли это уже сделано.. псевдо код после

take x and y
calculate spline for each three points 
x[0], x[1], x[2] ... x[1], x[2], x[3] ... and so on
for each y[n] sums every computation done for it and divide by number of 
computations (i.e. y[1] is computed for triplette x[0..2] and x[1..3] so the 
sum is divided by two (average for each point is taken as its value)
8
matplotlib numpy python scipy spline

5 ответов

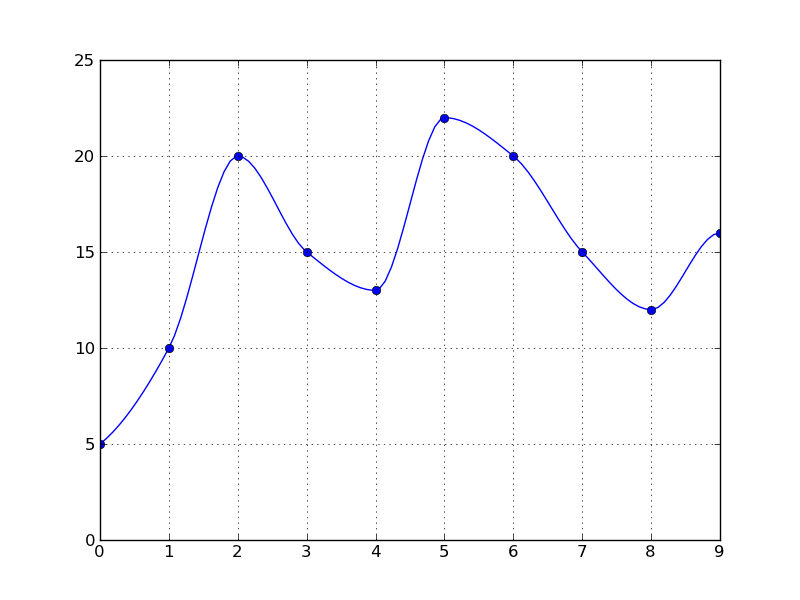
для этого типа графика вы хотите монотонная интерполяция. The PchipInterpolator class (который вы можете ссылаться на его более короткий псевдоним pchip) в scipy.интерполировать можно использовать:

import numpy as np
from scipy.interpolate import pchip
import matplotlib.pyplot as plt


# Data to be interpolated.
x = np.arange(10.0)
y = np.array([5.0, 10.0, 20.0, 15.0, 13.0, 22.0, 20.0, 15.0, 12.0, 16.0])

# Create the interpolator.
interp = pchip(x, y)

# Dense x for the smooth curve.
xx = np.linspace(0, 9.0, 101)

# Plot it all.
plt.plot(xx, interp(xx))
plt.plot(x, y, 'bo')
plt.ylim(0, 25)
plt.grid(True)
plt.show()

результат:

enter image description here

8

проблема не проблема дисплея. Это проблема интерполяции. Вы интерполяция с помощью сплайн-функции. Выбор правильного метода интерполяции очень сильно зависит от типа данных, которые у вас есть. Вы не можете ожидать, что функция интерполяции будет вести себя правильно в любых обстоятельствах (интерполяция не может знать, что ваша функция увеличивается).

1

вы должны посмотреть

scipy.интерполировать.LSQUnivariateSpline и играть с параметром k (степень сплайна)

или scipy.интерполировать.UnivariateSpline и играть с параметром k и s.

1

важно понимать, что интерполяция-это не просто линии для наглядности. Это математическая модель, представляющая, как вы думаете, ведет себя система (система, которая генерирует данные, которые вы измерили). Различные типы интерполяций представляют различные предположения о системе.

Итак, если вы знаете, что ваша система такова, что переменная может только увеличиваться, вы должны соответствовать соответствующей модели (т. е. использовать соответствующую интерполяцию). Глядя на ваши данные, похоже, полином 2-й степени или экспоненциальная функция могут хорошо подойти. Также будет работать loess (локальная регрессия). Вы можете использовать любые индивидуальные функции, такие как numpy.polyfit (), или общий штуцер кривой с scipy.оптимизировать.curve_fit(). Если у вас есть дополнительные знания о системе, вы должны использовать ее для выбора подходящей модели.

1

Я немного осмотрелся. То, что вы хотите называется

монотонная кубическая интерполяция,

посмотреть в Википедии здесь. У вас есть обсуждение mathexchange об этом здесь и я нашел реализацию в python здесь. Дайте мне знать, если это сработает!

1