Как построить матрицу смежности с помощью MATLAB

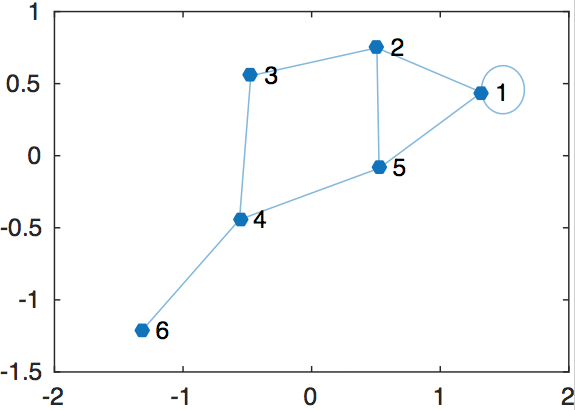
Я хочу создать график, показывающий связи между узлами из матрицы смежности, как показано ниже.

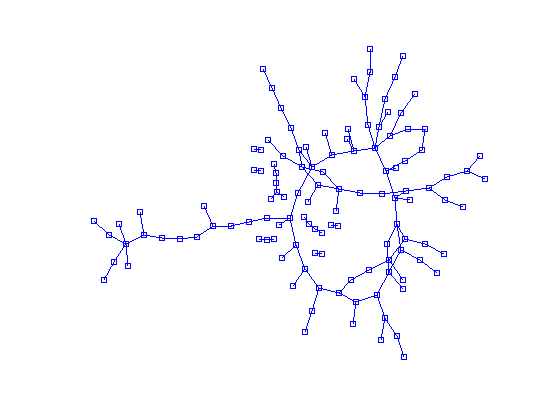
enter image description here

gplot кажется лучшим инструментом для этого. Однако, чтобы использовать его, мне нужно передать координату каждого узла. Проблема в том, что я не знаю, где должны быть координаты, я надеялся, что функция сможет найти для меня хороший макет.

например вот мой вывод, используя следующие произвольные координаты:

 A = [1 1 0 0 1 0;
      1 0 1 0 1 0;
      0 1 0 1 0 0;
      0 0 1 0 1 1;
      1 1 0 1 0 0;
      0 0 0 1 0 0];

 crd = [0 1;
        1 1;
        2 1;
        0 2;
        1 2;
        2 2];

 gplot (A, crd, "o-");

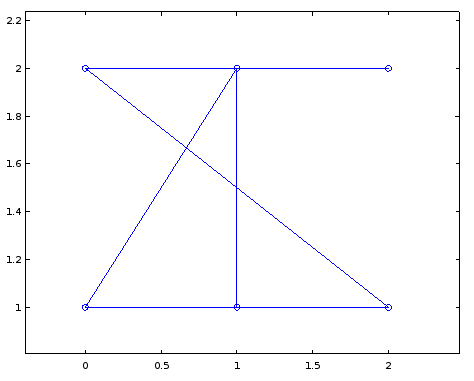
enter image description here

который трудно читать, но если я немного поиграю с координатами и изменю их на следующие, он станет намного более читаемым.

   crd = [0.5 0;
         0 1;
         0 2;
         1 2;
         1 1;
         1.5 2.5];

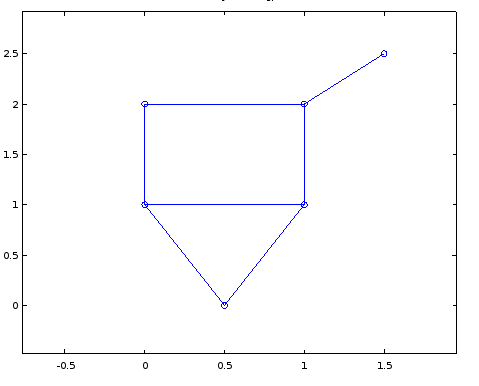
enter image description here

Я не ожидаю идеально оптимизированных координат или чего-то еще, но как я могу сказать MATLAB автоматически вычислить набор координат для меня, который выглядит нормально, используя какой-то алгоритм так что я могу график что-то похожее на верхнюю картинку.

спасибо заранее.

8
adjacency-matrix graph-theory matlab matrix octave

3 ответов

начиная с R2015b, MATLAB теперь имеет набор графовых и сетевых алгоритмов. Для этого примера вы можете создать неориентированный объект graph а затем построить его с помощью перегружен plot функции:

% Create symmetric adjacency matrix
A = [1 1 0 0 1 0;
     1 0 1 0 1 0;
     0 1 0 1 0 0;
     0 0 1 0 1 1;
     1 1 0 1 0 0;
     0 0 0 1 0 0];
% Create undirected graph object
G = graph(A);
% Plot
plot(G);

Layout created using MATLAB's graph/plot function

5

один из способов-написать свой собственный алгоритм, используя какое-то электростатическое отталкивание, так как в статье вы связаны. Возможно, это можно сделать менее чем в 40 строках Matlab (кажется другие пробовали). Но иногда лучше использовать внешние инструменты, чем делать все в Matlab. Лучший инструмент для рисования графиков, вероятно,Graphviz, который поставляется с набором инструментов для рисования различных графиков стиль. Для неориентированных графов используется neato. Я не знаю, какой алгоритм он использует для распределения узлов, но я думаю, что это что-то похожее на те, что в вашей статье (одна из ссылок даже упоминает Graphviz!).

входной сигнал для этих инструментов очень простой формат текста, который легок достаточно для генерации используя Matlab. Пример (это работает в linux, возможно, вам придется немного изменить его в windows):

% adjacency matrix
A = [1 1 0 0 1 0;
     1 0 1 0 1 0;
     0 1 0 1 0 0;
     0 0 1 0 1 1;
     1 1 0 1 0 0;
     0 0 0 1 0 0];

% node labels, these must be unique
nodes = {'A', 'B', 'C', 'D', 'E', 'F'};

n = length(nodes);
assert(all(size(A) == n))

% generate dot file for neato
fid = fopen('test.dot', 'w');
fprintf(fid, 'graph G {\n');
for i = 1:n
    for j = i:n
        if A(i, j)
            fprintf(fid, '    %s -- %s;\n', nodes{i}, nodes{j});
        end
    end
end
fprintf(fid, '}\n');
fclose(fid);

% render dot file
system('neato -Tpng test.dot -o test.png')

что дает файл :

graph G {
    A -- A;
    A -- B;
    A -- E;
    B -- C;
    B -- E;
    C -- D;
    D -- E;
    D -- F;
}

и, наконец, изображение

5

Если ваш граф связан, способ построить массив xy для перехода в gplot равен v(:,[2 3]), где v-матрица собственных векторов матрицы Лапласа, упорядоченная от наименьших собственных значений до наибольших. Поэтому мы можем сделать это так:

L=diag(sum(A))-A;
[v,~]=eig(L);
xy=v(:,[2 3])
gplot(A,xy)

или так:

L=diag(sum(A))-A;
[v,~]=eigs(L,3,'SM')
xy=v(:,[2 1])
gplot(A,xy)

второй должен быть более эффективным, особенно если большая.

это создаст хороший сюжет при нормальных обстоятельствах. Это не гарантировано для работы; в частности, это не гарантируется назначение разным узлам разных координат. Но обычно это работает довольно хорошо.

некоторую теорию за этим можно найти в https://arxiv.org/pdf/1311.2492.pdf

0