Как правильно использовать функции skew и kurtosis scipy?

на асимметричности - это параметр для измерения симметрии набора данных и эксцесс чтобы измерить, насколько тяжелы его хвосты по сравнению с нормальным распределением, см., например,здесь.

scipy.stats обеспечивает простой способ расчета этих двух величин, см. scipy.stats.kurtosis и scipy.stats.skew.

в моем понимании, асимметрия и эксцесс нормальное распределение оба должны быть 0, используя только что упомянутые функции. Однако это не относится к моему коду:

import numpy as np
from scipy.stats import kurtosis
from scipy.stats import skew

x = np.linspace( -5, 5, 1000 )
y = 1./(np.sqrt(2.*np.pi)) * np.exp( -.5*(x)**2  )  # normal distribution

print( 'excess kurtosis of normal distribution (should be 0): {}'.format( kurtosis(y) ))
print( 'skewness of normal distribution (should be 0): {}'.format( skew(y) ))

выход:

избыточный эксцесс нормального распределения (должен быть 0): -0.307393087742

асимметрия нормального распределения (должно быть 0): 1.11082371392

что я делаю не так ?

версии, которые я использую, являются

python: 2.7.6
scipy : 0.17.1
numpy : 1.12.1
10
numpy python scipy statistics

2 ответов

эти функции вычисляют моменты распределение плотности вероятности (поэтому он принимает только один параметр) и не заботится о "функциональной форме" значений.

они предназначены для " случайных наборов данных "(подумайте о них как о мерах, таких как среднее, стандартное отклонение, дисперсия):

import numpy as np
from scipy.stats import kurtosis, skew

x = np.random.normal(0, 2, 10000)   # create random values based on a normal distribution

print( 'excess kurtosis of normal distribution (should be 0): {}'.format( kurtosis(x) ))
print( 'skewness of normal distribution (should be 0): {}'.format( skew(x) ))

что дает:

excess kurtosis of normal distribution (should be 0): -0.024291887786943356
skewness of normal distribution (should be 0): 0.009666157036010928

изменение количества случайных значений повышает точность:

x = np.random.normal(0, 2, 10000000)

ведущий кому:

excess kurtosis of normal distribution (should be 0): -0.00010309478605163847
skewness of normal distribution (should be 0): -0.0006751744848755031

в вашем случае функция "предполагает", что каждое значение имеет одинаковую" вероятность " (потому что значения распределены поровну и каждое значение происходит только один раз), поэтому с точки зрения skew и kurtosis он имеет дело с негауссовой плотностью вероятности (не уверен, что именно это такое), что объясняет, почему результирующие значения даже не близки к 0:

import numpy as np
from scipy.stats import kurtosis, skew

x_random = np.random.normal(0, 2, 10000)

x = np.linspace( -5, 5, 10000 )
y = 1./(np.sqrt(2.*np.pi)) * np.exp( -.5*(x)**2  )  # normal distribution

import matplotlib.pyplot as plt

f, (ax1, ax2) = plt.subplots(1, 2)
ax1.hist(x_random, bins='auto')
ax1.set_title('probability density (random)')
ax2.hist(y, bins='auto')
ax2.set_title('(your dataset)')
plt.tight_layout()

enter image description here

11

вы используете в качестве данных "форму" функции плотности. Эти функции предназначены для использования с данными выборки из распределения. При выборке из распределения будет получена статистика выборки, которая приблизится к правильному значению по мере увеличения размера выборки. Для построения графика данных я бы рекомендовал гистограмму.

%matplotlib inline
import numpy as np
import pandas as pd
from scipy.stats import kurtosis
from scipy.stats import skew

import matplotlib.pyplot as plt

plt.style.use('ggplot')

data = np.random.normal(0, 1, 10000000)
np.var(data)

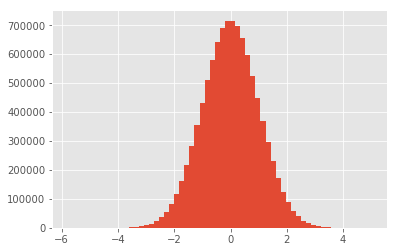
plt.hist(data, bins=60)

print("mean : ", np.mean(data))
print("var  : ", np.var(data))
print("skew : ",skew(data))
print("kurt : ",kurtosis(data))

выход:

mean :  0.000410213500847
var  :  0.999827716979
skew :  0.00012294118186476907
kurt :  0.0033554829466604374

enter image description here

Если вы имеете дело с аналитическим выражением, это крайне маловероятно, что вы получите ноль при использовании данных.

3