Как правильно триангулировать полигон в C++
Я работаю над триангуляцией объекта (в конечном счете, я хочу реализовать триангуляцию Делоне, но триангуляция не работает даже до легализации ребер, поэтому я хотел бы сначала сосредоточиться на простой триангуляции). Я включаю соответствующий код ниже. Я реализую метод триангуляции, аналогичный описанному в "вычислительной геометрии: алгоритмы и приложение третье издание" Марка де Берга, среди других. Ниже приведен псевдокод (я удалю его, если нужно быть):
Примечание: Я изменил псевдо-код, создав граничный треугольник вместо использования "лексикографически высшей точки P", потому что я не был слишком уверен, как определить p-1 и p-2 как говорится в учебнике, чтобы определить их "символически", а не определять точные единицы (конечно, возможно, что я просто неправильно понял, что он пытался сказать, чтобы быть справедливым). Кроме того, легализация не является частью моего кода (пока), поскольку это необходимо для Триангуляция Делоне, но я хочу убедиться, что простая триангуляция работает по назначению.
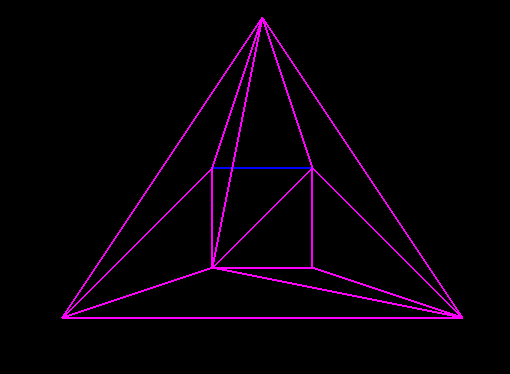
проблема в том, что я получаю некоторые триангуляции, такие как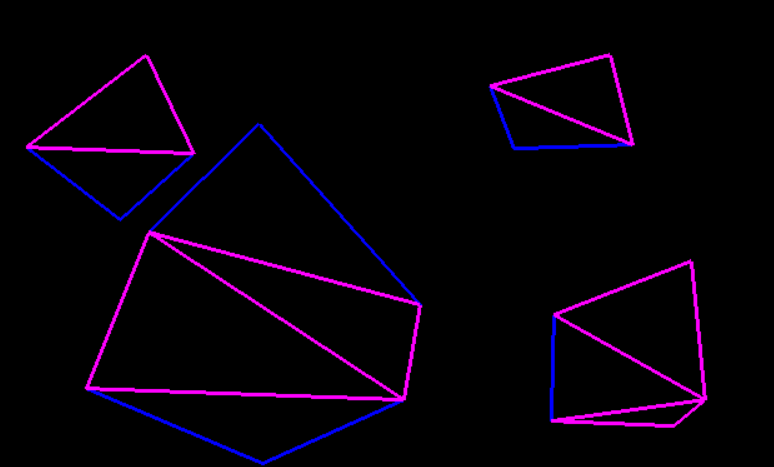 
где синие линии от исходного полигона.
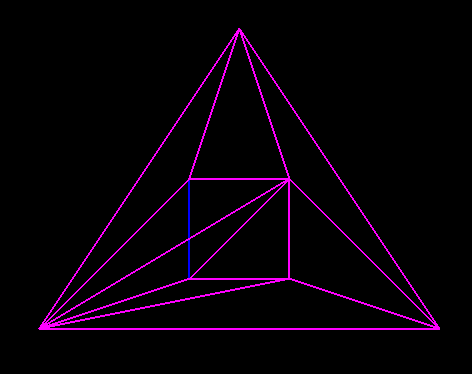
некоторые из этих линий не добавляются, потому что они являются частью треугольников точек p0, p1 и p2, которые я не добавляю в метод findSmallest. Тем не менее, если я добавлю эти треугольники, я получу что-то вроде этого: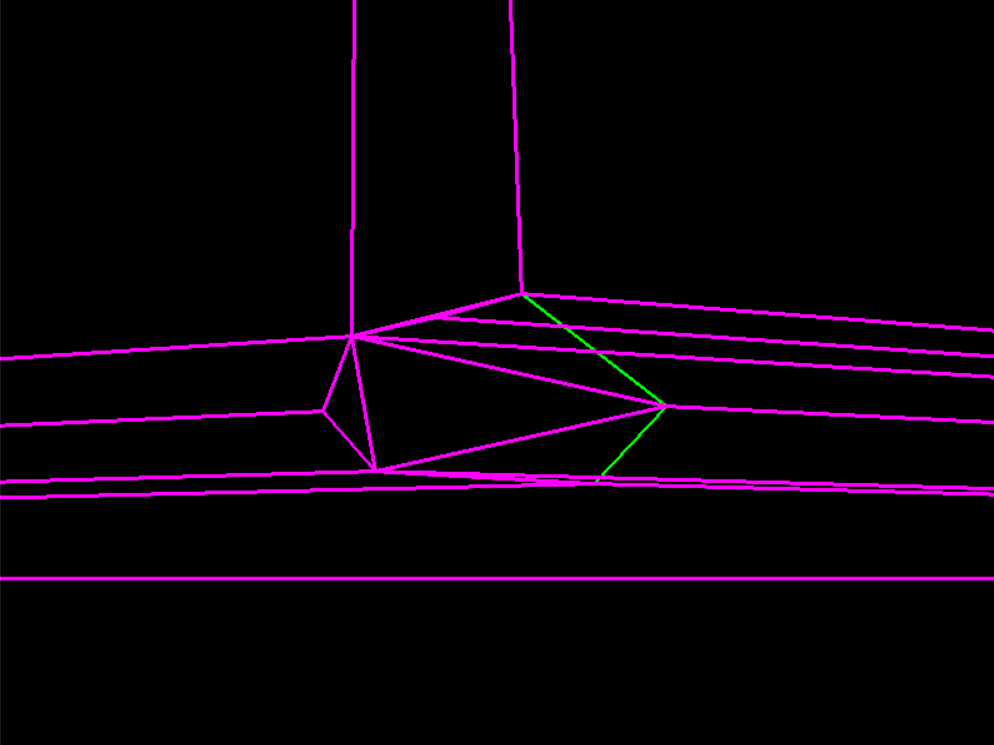
(Примечание p0, p1 и p2 находятся за пределами размах картины). Некоторые линии из исходного полигона (на этот раз зеленого цвета) все еще не добавлены в триангуляцию. Я не знаю, где я ошибаюсь.
Я надеюсь, что код понятен, но я собираюсь объяснить некоторые методы / структуры на всякий случай:
TriPoint
является дочерним элементом структуры Point.
p0, p1, p2
три точки образуют ограничивающий треугольник вокруг многоугольника. Я получил эту идею от этот пост.
contains(Point p)
возвращает true, если точка находится внутри треугольника или на одной из кромок.
findCommonTriangle(TriPoint *a, TriPoint *b, Triangle *t)
возвращает инцидент треугольника в t вдоль края ab. (Я не использую ребра для вычисления триангуляции, поэтому я решил получить инцидентный треугольник таким образом).
isOnTriangle(Point s)
вызывается на треугольнике abc и возвращает 1, если точка находится на краю ab, 2, Если pointis на краю bc, 3, если точка находится на краю cd. Если он находится внутри треугольника, он возвращается 0.
код для самой триангуляции находится ниже:
#include <GLglew.h>
#include <GLfreeglut.h>
#include <iostream>
#include <array>
#include <vector>
#include "predicates.h"
struct Point {
float x, y;
Point() { }
Point(float a, float b) {
x = a;
y = b;
}
};
struct Triangle;
struct Triangulation;
std::vector<Triangulation *> triangulations;
struct TriPoint : Point {
std::vector<Triangle *> triangles;
TriPoint() { };
int index;
TriPoint(Point a) {
x = a.x;
y = a.y;
}
TriPoint(float x, float y) : Point(x, y) {};
void removeTriangle(Triangle *t) {
for (size_t i = 0; i < triangles.size(); i++) {
if (triangles[i] == t) {
triangles.erase(triangles.begin() + i);
}
}
}
void addTriangle(Triangle *t) {
triangles.push_back(t);
}
};
double pointInLine(Point *a, Point *b, Point *p) {
REAL *A, *B, *P;
A = new REAL[2];
B = new REAL[2];
P = new REAL[2];
A[0] = a->x;
A[1] = a->y;
B[0] = b->x;
B[1] = b->y;
P[0] = p->x;
P[1] = p->y;
double orient = orient2d(A, B, P);
delete(A);
delete(B);
delete(P);
return orient;
}
struct Triangle {
TriPoint *a, *b, *c;
std::vector<Triangle *> children;
Triangle() { };
Triangle(TriPoint *x, TriPoint *y, TriPoint *z) {
a = x;
b = y;
c = z;
orientTri();
x->addTriangle(this);
y->addTriangle(this);
z->addTriangle(this);
}
bool hasChildren() {
return children.size() != 0;
}
void draw() {
glBegin(GL_LINE_STRIP);
glVertex2f(a->x, a->y);
glVertex2f(b->x, b->y);
glVertex2f(c->x, c->y);
glVertex2f(a->x, a->y);
glEnd();
}
bool contains(Point s) {
float as_x = s.x - a->x;
float as_y = s.y - a->y;
bool s_ab = (b->x - a->x)*as_y - (b->y - a->y)*as_x > 0;
if ((c->x - a->x)*as_y - (c->y - a->y)*as_x > 0 == s_ab) return false;
if ((c->x - b->x)*(s.y - b->y) - (c->y - b->y)*(s.x - b->x) > 0 != s_ab) return false;
return true;
}
int isOnTriangle(Point p) {
//Return -1 if outside
//Returns 1 if on AB
//Returns 2 if on BC
//Returns 3 if on CA
//Returns 4 if on B
//Returns 5 if on C
//Returns 6 if on A
double res1 = pointInLine(b, a, &p);
double res2 = pointInLine(c, b, &p);
double res3 = pointInLine(a, c, &p);
/*If triangles are counter-clockwise oriented then a point is inside
the triangle if the three 'res' are < 0, at left of each oriented edge
*/
if (res1 > 0 || res2 > 0 || res3 > 0)
return -1; //outside
if (res1 < 0) {
if (res2 < 0) {
if (res3 < 0) {
return 0; //inside
} else { //res3 == 0
return 3; //on edge3
}
} else { //res2 == 0
if (res3 == 0) {
return 5; //is point shared by edge2 and edge3
}
return 2; //on edge2
}
} else { //res1 == 0
if (res2 == 0) {
return 4; //is point shared by edge1 and edge2
} else if (res3 == 0) {
return 6; //is point shared by edge1 and 3
}
return 1; //on edge 1
}
}
TriPoint *getThirdPoint(TriPoint *x, TriPoint *y) {
if (a != x && a != y)
return a;
if (b != x && b != y)
return b;
return c;
}
bool hasPoint(TriPoint *p) {
return a == p || b == p || c == p;
}
void orientTri() {
REAL *A, *B, *C;
A = new REAL[2];
B = new REAL[2];
C = new REAL[2];
A[0] = a->x;
A[1] = a->y;
B[0] = b->x;
B[1] = b->y;
C[0] = c->x;
C[1] = c->y;
double orientation = orient2d(A, B, C);
if (orientation < 0) {
TriPoint *temp = a;
a = b;
b = temp;
}
delete(A);
delete(B);
delete(C);
}
};
struct Poly {
std::vector<Point> points;
bool selected = false;
};
Triangle *findCommonTriangle(TriPoint *a, TriPoint *b, Triangle *t) {
//Returns a triangle shared by a and b incident to t
for (Triangle *aTri : a->triangles) {
for (Triangle *bTri : b->triangles) {
if (aTri == bTri && aTri != t) {
return aTri;
}
}
}
return NULL;
}
struct Triangulation {
std::vector<Point> points;
std::vector<Triangle *> triangles;
float xMin = 9999;
float xMax = 0;
float yMin;
float yMax;
Triangulation() { };
Triangulation(Poly p) {
points = p.points;
sort();
triangulate();
}
void draw() {
for (Triangle *t : triangles) {
t->draw();
}
}
void sort() {
//Sort by y-value in ascending order.
//If y-values are equal, sort by x in ascending order.
for (size_t i = 0; i < points.size() - 1; i++) {
if (points[i].x < xMin) {
xMin = points[i].x;
}
if (points[i].x > xMax) {
xMax = points[i].x;
}
int index = i;
for (size_t j = i; j < points.size(); j++) {
if (points[index].y > points[j].y) {
index = j;
} else if (points[index].y == points[j].y) {
if (points[index].x > points[j].x) {
index = j;
}
}
}
std::swap(points[i], points[index]);
}
yMin = points[0].y;
yMax = points[points.size() - 1].y;
std::random_shuffle(points.begin(), points.end());
}
void triangulate() {
Triangle *root;
float dx = xMax - xMin;
float dy = yMax - yMin;
float deltaMax = std::max(dx, dy);
float midx = (xMin + xMax) / 2.f;
float midy = (yMin + yMax) / 2.f;
TriPoint *p0;
TriPoint *p1;
TriPoint *p2;
p0 = new TriPoint(midx - 2 * deltaMax, midy - deltaMax);
p1 = new TriPoint(midx, midy + 2 * deltaMax);
p2 = new TriPoint(midx + 2 * deltaMax, midy - deltaMax);
p0->index = 0;
p1->index = -1;
p2->index = -2;
root = new Triangle(p0, p1, p2);
for (size_t i = 0; i < points.size(); i++) {
TriPoint *p = new TriPoint(points[i]);
p->index = i + 1;
Triangle *temp = root;
double in;
while (temp->hasChildren()) {
for (size_t j = 0; j < temp->children.size(); j++) {
in = temp->children[j]->isOnTriangle(points[i]);
if (in >= 0) {
temp = temp->children[j];
break;
}
}
}
in = temp->isOnTriangle(points[i]);
if (in > 0 ) { //Boundary
if (in == 1) { //AB
Triangle *other = findCommonTriangle(temp->a, temp->b, temp);
TriPoint *l = other->getThirdPoint(temp->a, temp->b);
l->removeTriangle(other);
temp->a->removeTriangle(other);
temp->b->removeTriangle(other);
temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);
Triangle *n1 = new Triangle(temp->a, p, temp->c);
Triangle *n2 = new Triangle(temp->b, temp->c, p);
Triangle *n3 = new Triangle(temp->a, l, p);
Triangle *n4 = new Triangle(temp->b, p, l);
temp->children.push_back(n1);
temp->children.push_back(n2);
other->children.push_back(n3);
other->children.push_back(n4);
} else if (in == 2) { //BC
Triangle *other = findCommonTriangle(temp->b, temp->c, temp);
TriPoint *l = other->getThirdPoint(temp->b, temp->c);
l->removeTriangle(other);
temp->b->removeTriangle(other);
temp->c->removeTriangle(other);
temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);
Triangle *n1 = new Triangle(temp->a, p, temp->c);
Triangle *n2 = new Triangle(temp->b, temp->a, p);
Triangle *n3 = new Triangle(temp->c, p, l);
Triangle *n4 = new Triangle(temp->b, l, p);
temp->children.push_back(n1);
temp->children.push_back(n2);
other->children.push_back(n3);
other->children.push_back(n4);
} else if (in == 3) { //CA
Triangle *other = findCommonTriangle(temp->a, temp->c, temp);
TriPoint *l = other->getThirdPoint(temp->a, temp->c);
l->removeTriangle(other);
temp->a->removeTriangle(other);
temp->c->removeTriangle(other);
temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);
Triangle *n1 = new Triangle(temp->b, temp->c, p);
Triangle *n2 = new Triangle(temp->a, temp->b, p);
Triangle *n3 = new Triangle(temp->c, l, p);
Triangle *n4 = new Triangle(temp->a, p, l);
temp->children.push_back(n1);
temp->children.push_back(n2);
other->children.push_back(n3);
other->children.push_back(n4);
}
} else { //Point is inside of triangle
Triangle *t1 = new Triangle(temp->a, temp->b, p);
Triangle *t2 = new Triangle(temp->b, temp->c, p);
Triangle *t3 = new Triangle(temp->c, temp->a, p);
temp->a->removeTriangle(temp);
temp->b->removeTriangle(temp);
temp->c->removeTriangle(temp);
temp->children.push_back(t1);
temp->children.push_back(t2);
temp->children.push_back(t3);
}
} //Triangulation done
findSmallest(root, p0, p1, p2);
triangulations.push_back(this);
}
void findSmallest(Triangle *root, TriPoint *p0, TriPoint *p1, TriPoint *p2) {
bool include = true; //Controls drawing triangles with p0, p1, and p2
if (root->hasChildren()) {
for (Triangle *t : root->children) {
findSmallest(t, p0, p1, p2);
}
} else {
int i0 = root->hasPoint(p0);
int i1 = root->hasPoint(p1);
int i2 = root->hasPoint(p2);
if ((!i0 && !i1 && !i2) || include) {
triangles.push_back(root);
}
}
}
};
Poly polygon;
void changeViewPort(int w, int h)
{
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, glutGet(GLUT_WINDOW_WIDTH), 0, glutGet(GLUT_WINDOW_HEIGHT), -1, 1);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.375, 0.375, 0.0);
}
void render() {
glClear(GL_COLOR_BUFFER_BIT);
glLineWidth(2.5);
changeViewPort(glutGet(GLUT_WINDOW_WIDTH), glutGet(GLUT_WINDOW_HEIGHT));
glColor3f(0, 0, 1); //Blue
glBegin(GL_LINE_STRIP);
for (size_t j = 0; j < polygon.points.size(); j++) {
std::vector<Point> ps = polygon.points;
Point p1 = ps[j];
glVertex2i(p1.x, p1.y);
}
glVertex2i(polygon.points[0].x, polygon.points[0].y);
glEnd();
glColor3f(1, 0, 1);
for (Triangulation *t : triangulations) {
t->draw();
}
glutSwapBuffers();
}
int main(int argc, char* argv[]) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA | GLUT_DEPTH);
glutInitWindowSize(800, 600);
glutCreateWindow("Stack Overflow Question");
glutReshapeFunc(changeViewPort);
glutDisplayFunc(render);
exactinit();
polygon.points.push_back(*new Point(300.0f, 300.0f));
polygon.points.push_back(*new Point(300.0f, 400.0f));
polygon.points.push_back(*new Point(400.0f, 400.0f));
polygon.points.push_back(*new Point(400.0f, 300.0f));
Triangulation t = *(new Triangulation(polygon));
glutMainLoop();
return 0;
}
Примечание: предикаты.cpp и предикаты.h были созданы с использованием кода из здесь.
2 ответов
ваш код довольно неоптимален, но теперь это не имеет значения (вы учитесь, верно?. Я сосредоточусь на вопросах триангуляции.
отредактировано: вы инициализируете yMin и yMax члены Triangulation at sort() и используйте их позже для" большого охватывающего " треугольника. Если вы решите не использовать " sort ()", вы будете использовать инициализированные значения. Установите некоторые значения по умолчанию.
сортировка точек не требуется для построения триангуляции. Вы используйте его просто, чтобы найти BB, слишком много усилий, и в конце перетасовать их, снова слишком много усилий.
главная проблема (в вашем первом посте, прежде чем вы отредактировали его) я вижу способ найти, находится ли точка внутри треугольника, на его границе или вне его.
Triangle::isOnTriangle() - это ужасно. Вы вычисляете несколько crossproducts и return ' 0 '(внутри треугольника) ни один из них не равен "0".
вы можете утверждать, что заранее знаете, что дело в не снаружи, потому что вы тестировали его раньше Triangle::contains(), но эта функция также ужасна, не так много, хотя.
лучшие (или по крайней мере самый простой и наиболее используемый) способ найти относительное положение точки На линии
res = (y2 - y1)*(px - x1) - (x2 - x1)*(py - y1)
res является положительным значением, если {px,py} в праве {x1,y1} to {x2,y2} линии. Отрицательно, если слева и ноль, если на линии.
две важные вещи здесь:
- a) замена направления (т. е. строка
{x2,y2} to {x1,y1}) изменяет знакres. - b) говоря, если
resдействительно ноль нелегко из-за числовых проблем, как и в любом другом представлении с плавающей точностью.
для a) вы должны быть уверены, что все треугольники имеют одинаковую ориентацию (или первое выражение будет использовано неправильно). Вы можете проявлять особую осторожность в порядке очков, которые вы передаете треугольнику ctor. Или вы можете добавить функцию "orientTri", которая их устанавливает. В настоящее время ограничивающий треугольник-по часовой стрелке. Наиболее распространенный порядок (также используемый в OpenGL) против часовой стрелки; но вы можете выбрать тот, который вам нравится, просто знайте об этом.
для b) сравнение поплавка с " 0 " не является хорошей идеей. В некоторых сценариях вы можете использовать if std::abs(value) < someEpsilon. Но особенно с триангуляциями этого недостаточно. примеры класс
Задачи устойчивости в геометрических вычислениях очень хорошо объясняет, почему ваши расчеты должны быть "прочный." Shewchuk Надежные Предикаты очень хорошее решение.
после того, как вы решили эти две темы, проблема "точки в треугольнике" может быть обработана следующим образом:
double pointInLine(line *L, point *p)
{
//returns positive, negative or exactly zero value
return robustCalculus(L, p);
}
int pointInTriangle(triangle *t, point *p)
{
double res1 = pointInLine(t->edge1, p);
double res2 = pointInLine(t->edge2, p);
double res3 = pointInLine(t->edge3, p);
/*If triangles are counter-clockwise oriented then a point is inside
the triangle if the three 'res' are < 0, at left of each oriented edge
*/
if ( res1 > 0 || res2 > 0 || res3 > 0 )
return -1; //outside
if ( res1 < 0 )
if ( res2 < 0 )
if ( res3 < 0 )
return 0; //inside
else //res3 == 0
return 3; //on edge3
else //res2 == 0
{ if ( res3 == 0 )
return 5; //is point shared by edge2 and edge3
return 2; //on edge2
}
else
... test for other edges or points
}
для остальной части процесса триангуляции несколько советов:
потому что вы хотите триангуляцию Делоне, каждый раз, когда вы добавляете новую точку, вы должны проверить условие "окружности" (нет другого треугольника, окружность которого содержит этот новый пункт). Это можно сделать, как показано в книге или в ссылках, которые я разместил. Опять же, вам нужно надежная предикаты.
Shuffling порядок вставки точек может улучшить производительность для определения местоположения треугольника, где лежит новая точка. Это может быть верно в зависимости от метода, используемого для размещения детали. Вы используете иерархию треугольников, поэтому, если данные отсортированы или нет, это не влияет.
кстати, поддержание иерархическая структура для каждого добавленного/удаленного/измененного треугольника стоит дорого в CPU и RAM. Возможно, вы найдете другой способ позже,когда получите опыт работы с сеткой.
без иерархии метод" ходить к точке " (google для него) кажется быстрее с рандомизированным входом. Но использование кэша (последнего построенного треугольника) намного эффективнее.
удачи с зацепления. Трудно начинать и отлаживать, дьявол живет в деталях.
Помимо вопросов, уже указанных в ответе Ripi2, я хотел бы предложить следующее:
1. random_shuffle:
Я вижу, что вы не инициализируете генератор случайных чисел (вызывая srand в Main функции). Это означает, что вы всегда будете использовать одну и ту же псевдослучайную последовательность, поэтому выполнение программы несколько раз приведет к одному и тому же результату. Я протестировал ваш код, и перетасовка действительно влияет на код. После правильно инициализируя генератор случайных чисел, вы можете видеть, что триангуляция меняется каждый раз, создавая разные треугольники.
2. сравнения:
в вашем коде вы сравниваете точки и треугольники, сравнивая указатели. Это означает, например, что две точки будут равны тогда и только тогда, когда они будут точно такой же структурой в памяти. Две точечные структуры с одинаковыми координатами будут считаться разными точками. Я не уверен, что это это то, что вы хотите получить или нет, поэтому я бы предложил подумать об этом.
3. треугольник вокруг многоугольника:
помимо жестко закодированного значения (20), я не понимаю, почему этот код должен производить допустимую триангуляцию. Вы создаете несколько треугольников над многоугольником, но они все поделитесь одной из этих 3 фиксированных точек за пределами треугольника.
вот снимок, уменьшающий параметр hardcoded до 2, чтобы соответствовать всем треугольникам в окне просмотра:
тот же код, другой порядок точек (после инициализации srand со временем (0)):
У меня нет доступа к псевдокоду алгоритма, но я бы предложил отредактировать ваш ответ, чтобы кратко описать его, просто для ясности.
удачи в реализации :)