Как преодолеть особенности численного интегрирования (в Matlab или Mathematica)

Я хочу численно интегрировать следующее:

eq1

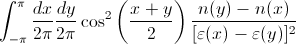
здесь

eq2

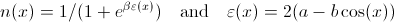
и a, b и β являются константами, которые для простоты могут быть установлены в 1.

ни Matlab, используя dblquad, ни Mathematica, используя NIntegrate может иметь дело с сингулярностью, созданной знаменателем. Поскольку это двойной Интеграл, я не могу указать, где сингулярность находится в Mathematica.

Я конечно, он не бесконечен, так как этот Интеграл основан на теории возмущений и без

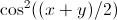
enter image description here

был найден раньше (только не мной, поэтому я не знаю, как это делается).

какие идеи?

8
matlab numerical-integration wolfram-mathematica

4 ответов

(1) было бы полезно, если бы вы предоставили явный код, который вы используете. Таким образом, другим (читай: мне) не нужно кодировать его отдельно.

(2) Если Интеграл существует, то он должен быть равен нулю. Это потому, что вы отрицаете фактор n(y)-n(x), когда вы меняете x и y, но сохраняете остальные те же. Тем не менее симметрия диапазона интеграции означает, что это просто переименование переменных, поэтому оно должно оставаться неизменным.

(3) вот некоторый код, который показывает, что он будет равен нулю, по крайней мере, если мы вычеркните единственную часть и небольшую полосу вокруг нее.

a = 1;
b = 1;
beta = 1;
eps[x_] := 2*(a-b*Cos[x])
n[x_] := 1/(1+Exp[beta*eps[x]])
delta = .001;
pw[x_,y_] := Piecewise[{{1,Abs[Abs[x]-Abs[y]]>delta}}, 0]

мы добавляем 1 к интегралу, чтобы избежать проблем с точностью с результатами, близкими к нулю.

NIntegrate[1+Cos[(x+y)/2]^2*(n[x]-n[y])/(eps[x]-eps[y])^2*pw[Cos[x],Cos[y]],
  {x,-Pi,Pi}, {y,-Pi,Pi}] / (4*Pi^2)

Я получаю результат ниже.

NIntegrate::slwcon: 
   Numerical integration converging too slowly; suspect one of the following:
    singularity, value of the integration is 0, highly oscillatory integrand,
    or WorkingPrecision too small.

NIntegrate::eincr: 
   The global error of the strategy GlobalAdaptive has increased more than 
    2000 times. The global error is expected to decrease monotonically after a
     number of integrand evaluations. Suspect one of the following: the
     working precision is insufficient for the specified precision goal; the
     integrand is highly oscillatory or it is not a (piecewise) smooth
     function; or the true value of the integral is 0. Increasing the value of
     the GlobalAdaptive option MaxErrorIncreases might lead to a convergent
     numerical integration. NIntegrate obtained 39.4791 and 0.459541
     for the integral and error estimates.

Out[24]= 1.00002

это хороший признак того, что чистый результат будет равен нулю.

(4) Замена CX на cos(x) и cy на cos(y) и удаление посторонних факторов для целей оценки сходимости дает выражение под.

((1 + E^(2*(1 - cx)))^(-1) - (1 + E^(2*(1 - cy)))^(-1))/
 (2*(1 - cx) - 2*(1 - cy))^2

расширение серии в cy, центрированное на cx, указывает на полюс порядка 1. Таким образом, он кажется сингулярным интегралом.

Даниил Лихтблау

9

Интеграл выглядит как Интеграл типа главного значения Коши (т. е. он имеет сильную особенность). Вот почему вы не можете применять стандартные квадратурные методы.

вы пробовали PrincipalValue - > True в интеграции Mathematica?

2

в дополнение к наблюдению Даниэля об интегрировании нечетного интеграла в симметричном диапазоне (так что симметрия указывает, что результат должен быть равен нулю), вы также можете сделать это, чтобы лучше понять его сходимость (я буду использовать latex, написание этого с помощью пера и бумаги должно облегчить чтение; это заняло намного больше времени, чем писать, это не так сложно):

во-первых,epsilon(x)-\epsilon(y)\propto\cos(y)-\cos(x)=2\sin(\xi_+)\sin(\xi_-) где я определил \xi_\pm=(x\pm y)/2 (поэтому я повернул оси на pi / 4). В области интеграции тогда это \xi_+ между \pi/\sqrt{2} и -\pi/\sqrt{2} и \xi_- между \pm(\pi/\sqrt{2}-\xi_-). Тогда Интеграл принимает вид \frac{1}{\sin^2(\xi_-)\sin^2(\xi_+)} времена термины без расхождений. Итак, очевидно, существуют полюса второго порядка, и это не сходится, как представлено.

возможно, вы могли бы написать людям, которые получили ответ с термином cos и спросить, что именно они сделали. Возможно, используется физическая регуляризация. Или вы могли бы дать больше информации о физической происхождение этого (какая-то теория возмущений второго порядка для какой-то бозонной системы?), если бы это не было вне темы...

1

может быть, я что-то упускаю здесь, но integrand f[x, y]=Cos^2 [(x+y)/2]*(n[x]-n[y])/(eps[x]-eps[y]) с n[x]=1/(1+Exp[Beta*eps[x]]) и eps[x]=2 (a-b*Cos[x]) действительно является симметричной функцией в x и y: f[x, - y]= f [- x, y]=f[x,y]. Поэтому его Интеграл над любой областью [- u,u]x [- v,v] равен нулю. Численное интегрирование здесь не требуется. Результат просто нулевой.

1