Как реализовать двудольный Граф в Java?

ПОПРОБУЙТЕ ЭТО:--

Bipartite.java

/*************************************************************************
 *  Compilation:  javac Bipartite.java
 *  Dependencies: Graph.java 
 *
 *  Given a graph, find either (i) a bipartition or (ii) an odd-length cycle.
 *  Runs in O(E + V) time.
 *
 *
 *************************************************************************/

/**
 *  The <tt>Bipartite</tt> class represents a data type for 
 *  determining whether an undirected graph is bipartite or whether
 *  it has an odd-length cycle.
 *  The <em>isBipartite</em> operation determines whether the graph is
 *  bipartite. If so, the <em>color</em> operation determines a
 *  bipartition; if not, the <em>oddCycle</em> operation determines a
 *  cycle with an odd number of edges.
 *  <p>
 *  This implementation uses depth-first search.
 *  The constructor takes time proportional to <em>V</em> + <em>E</em>
 *  (in the worst case),
 *  where <em>V</em> is the number of vertices and <em>E</em> is the number of edges.
 *  Afterwards, the <em>isBipartite</em> and <em>color</em> operations
 *  take constant time; the <em>oddCycle</em> operation takes time proportional
 *  to the length of the cycle.
 */
public class Bipartite {
    private boolean isBipartite;   // is the graph bipartite?
    private boolean[] color;       // color[v] gives vertices on one side of bipartition
    private boolean[] marked;      // marked[v] = true if v has been visited in DFS
    private int[] edgeTo;          // edgeTo[v] = last edge on path to v
    private Stack<Integer> cycle;  // odd-length cycle

    /**
     * Determines whether an undirected graph is bipartite and finds either a
     * bipartition or an odd-length cycle.
     * @param G the graph
     */
    public Bipartite(Graph G) {
        isBipartite = true;
        color  = new boolean[G.V()];
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];

        for (int v = 0; v < G.V(); v++) {
            if (!marked[v]) {
                dfs(G, v);
            }
        }
        assert check(G);
    }

    private void dfs(Graph G, int v) { 
        marked[v] = true;
        for (int w : G.adj(v)) {

            // short circuit if odd-length cycle found
            if (cycle != null) return;

            // found uncolored vertex, so recur
            if (!marked[w]) {
                edgeTo[w] = v;
                color[w] = !color[v];
                dfs(G, w);
            } 

            // if v-w create an odd-length cycle, find it
            else if (color[w] == color[v]) {
                isBipartite = false;
                cycle = new Stack<Integer>();
                cycle.push(w);  // don't need this unless you want to include start vertex twice
                for (int x = v; x != w; x = edgeTo[x]) {
                    cycle.push(x);
                }
                cycle.push(w);
            }
        }
    }

    /**
     * Is the graph bipartite?
     * @return <tt>true</tt> if the graph is bipartite, <tt>false</tt> otherwise
     */
    public boolean isBipartite() {
        return isBipartite;
    }

    /**
     * Returns the side of the bipartite that vertex <tt>v</tt> is on.
     * param v the vertex
     * @return the side of the bipartition that vertex <tt>v</tt> is on; two vertices
     *    are in the same side of the bipartition if and only if they have the same color
     * @throws UnsupportedOperationException if this method is called when the graph
     *    is not bipartite
     */
    public boolean color(int v) {
        if (!isBipartite)
            throw new UnsupportedOperationException("Graph is not bipartite");
        return color[v];
    }

    /**
     * Returns an odd-length cycle if the graph is not bipartite, and
     * <tt>null</tt> otherwise.
     * @return an odd-length cycle (as an iterable) if the graph is not bipartite
     *    (and hence has an odd-length cycle), and <tt>null</tt> otherwise
     */
    public Iterable<Integer> oddCycle() {
        return cycle; 
    }

    private boolean check(Graph G) {
        // graph is bipartite
        if (isBipartite) {
            for (int v = 0; v < G.V(); v++) {
                for (int w : G.adj(v)) {
                    if (color[v] == color[w]) {
                        System.err.printf("edge %d-%d with %d and %d in same side of bipartition\n", v, w, v, w);
                        return false;
                    }
                }
            }
        }

        // graph has an odd-length cycle
        else {
            // verify cycle
            int first = -1, last = -1;
            for (int v : oddCycle()) {
                if (first == -1) first = v;
                last = v;
            }
            if (first != last) {
                System.err.printf("cycle begins with %d and ends with %d\n", first, last);
                return false;
            }
        }

        return true;
    }

    /**
     * Unit tests the <tt>Bipartite</tt> data type.
     */
    public static void main(String[] args) {
        // create random bipartite graph with V vertices and E edges; then add F random edges
        int V = Integer.parseInt(args[0]);
        int E = Integer.parseInt(args[1]);
        int F = Integer.parseInt(args[2]);

        Graph G = new Graph(V);
        int[] vertices = new int[V];
        for (int i = 0; i < V; i++) vertices[i] = i;
        StdRandom.shuffle(vertices);
        for (int i = 0; i < E; i++) {
            int v = StdRandom.uniform(V/2);
            int w = StdRandom.uniform(V/2);
            G.addEdge(vertices[v], vertices[V/2 + w]);
        }

        // add F extra edges
        for (int i = 0; i < F; i++) {
            int v = (int) (Math.random() * V);
            int w = (int) (Math.random() * V);
            G.addEdge(v, w);
        }

        StdOut.println(G);

        Bipartite b = new Bipartite(G);
        if (b.isBipartite()) {
            StdOut.println("Graph is bipartite");
            for (int v = 0; v < G.V(); v++) {
                StdOut.println(v + ": " + b.color(v));
            }
        }
        else {
            StdOut.print("Graph has an odd-length cycle: ");
            for (int x : b.oddCycle()) {
                StdOut.print(x + " ");
            }
            StdOut.println();
        }
    }
}

это реализация c#, но концепция также может использоваться в Java. Я использовал матрицу смежности для представления графа. Проверка наличия цикла нечетный цикл на графике.

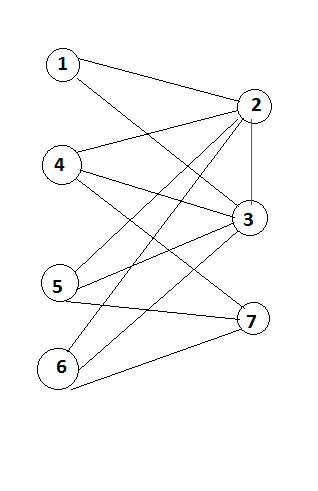
Граф называется двудольным, если в этом графе существует раздел, скажем u и v, где (U union v) = Graph и (U intersection v ) = null если вы рассматриваете рисунок ниже 1,2,3,4,5,6,7 являются вершинами в графе G. давайте рассмотрим вершины слева (1,4,5,6) как U и справа (2,3,7) как V

считай нет красный подключение в график сейчас. Вы могли видеть, что существует связь от u до v и v до u как его неориентированный граф. но нет никакой связи с разделом. Это концепция, которую я собираюсь использовать.

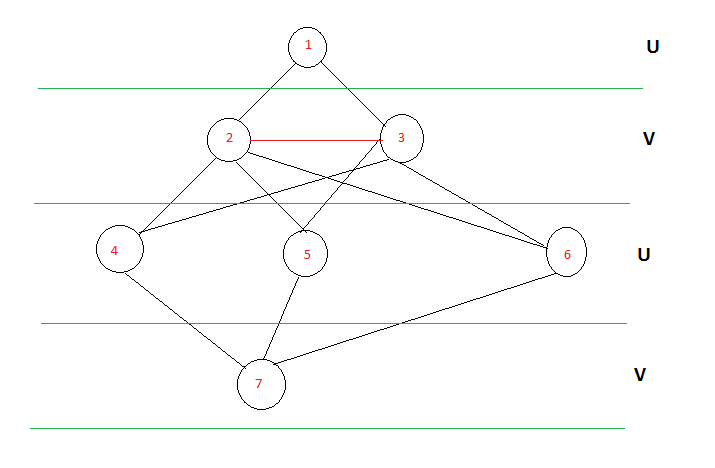
рассмотрим график, как показано ниже, тот же график выше, за исключением того, что он нарисован больше как древовидная структура. В этом случае, если вы можете видеть узлы, присутствующие на альтернативных уровнях 1,3,5, могут вместе сформировать раздел и 2,4 могут сформировать другой раздел. Поэтому мы можем легко сказать, что график двудольный. Что если есть красный край между элементами на одном уровне? тогда граф не двудольный.Если вы можете изменить алгоритм BFS, мы можем достичь этого.

вот код для этого.

   int[,] BPGraph = new int[7,7]{
                                    {0,1,0,1,0,0,0},
                                    {1,0,1,0,1,1,0},
                                    {0,1,0,1,0,0,1},
                                    {1,0,1,0,1,1,0},
                                    {0,1,0,1,0,0,1},
                                    {0,1,0,1,0,0,1},
                                    {0,0,1,0,1,1,0}
                                };

    int[] BPArray = new int[7] { 0, 0, 0, 0, 0, 0, 0 };

    public Boolean BiPartite()
    {
        Queue<int> VertexQueue = new Queue<int>();
        int level = 0;
        int nextlevel=0;
        Boolean BPFlg = true;

        VertexQueue.Enqueue(0);

        while(VertexQueue.Count!=0)
        {
            int current = VertexQueue.Dequeue();
            level = BPArray[current];

            if (level == 0)
                level = 1;

            if (level == 2)
                nextlevel=1;
            else
                nextlevel=2;

            if(BPArray[current]==0) 
                BPArray[current] = level;

            for (int i = 0; i < 7; i++)
            {
                if (BPGraph[current, i] == 1)
                {
                    if (BPArray[i] == 0)
                    {
                        BPArray[i] = nextlevel;
                        VertexQueue.Enqueue(i);
                    }
                    else if (BPArray[i] == level)
                    {
                        BPFlg = false;
                        break;
                    }
                }
            }
            if (!BPFlg)
                break;
        }
        return BPFlg;

    }

ориентированный граф-это тот, в котором ребро, соединяющее узлы A и B, имеет направление; если есть ребро от A до B, это не означает, что есть ребро от B до A. В вашем примере ребра имеют направление. (B-D будет два ребра, один от B до D и один от D до B.)

один из способов реализации этого будет аналогичен связанному списку, при этом узлы будут иметь ссылки друг на друга по мере необходимости. Возвращаясь к вашему примеру, nodeA будет иметь ссылку на nodeB, но не наоборот. nodeE будет иметь ссылку на nodeA и nodeC и так далее. Вы действительно создаете (своего рода) структуру данных, которая имеет понятие узлов и, возможно, ребер. Есть несколько способов, которыми вы могли бы это сделать.

возможной реализацией Java будет класс с именем AdjacencyList что есть Map<Vertex, List<Vertex>> содержащий вершину и ее смежные вершины. AdjacencyList затем иметь возможность выполнять операции на своей карте.

As для алгоритмов и вещей, чтобы иметь в виду, взгляните на свойства двудольных графов на Википедия, особенно

• граф двудольный тогда и только тогда, когда он не содержит нечетного цикла. Поэтому двудольный граф не может содержать клику размером 3 или более.
• каждое дерево является двудольным.
• циклические графы с четным числом вершин являются двудольными.

хорошим тестом будет реализация 2-алгоритм раскраски, чтобы подтвердить, что граф действительно двудольный. Глубина первого поиска, широта первого поиска являются хорошими упражнениями реализации.

1.) Выберите случайный узел. Поместите его в" левую " часть двудольного графика.

2.) Выберите все узлы, прилегающие к узлу, который вы выбрали в 1, и поместите их все в "правую" сторону.

3.) Остальные узлы принадлежат "левой" стороне двудольного графа.

конец