Как реализовать кривую Безье в C++?

Я хотел бы реализовать кривой Безье. Я делал это на C# раньше, но я совершенно не знаком с библиотеками c++. Как мне создать квадратичную кривую?

void printQuadCurve(float delta, Vector2f p0, Vector2f p1, Vector2f p2);

очевидно, что нам нужно использовать линейную интерполяцию, но существует ли это в стандартной математической библиотеке? Если нет, то где я могу его найти?

обновление 1:

Извините, я забыл упомянуть, что использую Linux.

12
c++ interpolation math spline

5 ответов

вы использовали библиотеку C# ранее?

в C++ стандартная библиотечная функция для кривых Безье недоступна (пока). Вы можете, конечно, свернуть свой собственный (CodeProject пример) или найдите математическую библиотеку.

этой blogpost объясняет идею красиво, но в Actionscript. Перевод не должен быть большой проблемой.

5

недавно я столкнулся с тем же вопросом и хотел реализовать его самостоятельно. Это изображение из Википедии помогло мне:

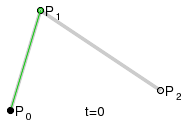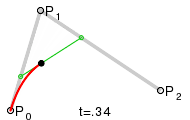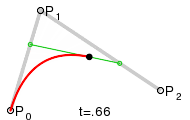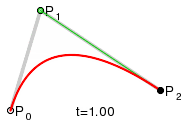
http://upload.wikimedia.org/wikipedia/commons/3/35/Bezier_quadratic_anim.gif

следующий код написан на C++ и показывает, как вычислить квадратичный Безье. 

int getPt( int n1 , int n2 , float perc )
{
    int diff = n2 - n1;

    return n1 + ( diff * perc );
}    

for( float i = 0 ; i < 1 ; i += 0.01 )
{
    // The Green Line
    xa = getPt( x1 , x2 , i );
    ya = getPt( y1 , y2 , i );
    xb = getPt( x2 , x3 , i );
    yb = getPt( y2 , y3 , i );

    // The Black Dot
    x = getPt( xa , xb , i );
    y = getPt( ya , yb , i );

    drawPixel( x , y , COLOR_RED );
}

С (x1|y1), (x2|y2) и (x3 / y3), являющимися P0, P1 и P2 на изображении. Просто чтобы показать основную идею...

для тех, кто просит кубический Безье, он просто работает аналоговый (также от Википедия):

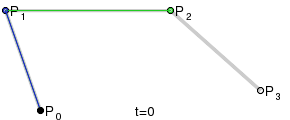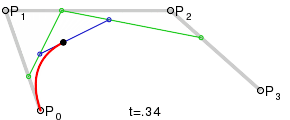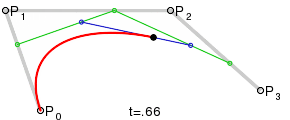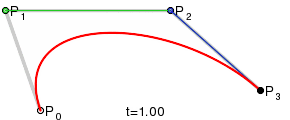
http://upload.wikimedia.org/wikipedia/commons/a/a3/Bezier_cubic_anim.gif

этой ответ содержит код для него.

93

вот общая реализация для кривой с любым количеством точек.

vec2 getBezierPoint( vec2* points, int numPoints, float t ) {
    vec2* tmp = new vec2[numPoints];
    memcpy(tmp, points, numPoints * sizeof(vec2));
    int i = numPoints - 1;
    while (i > 0) {
        for (int k = 0; k < i; k++)
            tmp[k] = tmp[k] + t * ( tmp[k+1] - tmp[k] );
        i--;
    }
    vec2 answer = tmp[0];
    delete[] tmp;
    return answer;
}

обратите внимание, что он использует память кучи для временного массива, который не так эффективен. Если вам нужно только иметь дело с фиксированным количеством точек, вы можете жестко закодировать значение numPoints и использовать память стека.

конечно, вышеизложенное предполагает, что у вас есть структура vec2 и операторы для нее так:

struct vec2 {
    float x, y;
    vec2(float x, float y) : x(x), y(y) {}
};

vec2 operator + (vec2 a, vec2 b) {
    return vec2(a.x + b.x, a.y + b.y);
}

vec2 operator - (vec2 a, vec2 b) {
    return vec2(a.x - b.x, a.y - b.y);
}

vec2 operator * (float s, vec2 a) {
    return vec2(s * a.x, s * a.y);
}
9

у вас есть выбор между методом де Кастельжау, который заключается в рекурсивном разделении пути управления до тех пор, пока вы не прибудете в точку с помощью линейной интерполяции, как описано выше, или методом Безье, который заключается в смешивании контрольных точек.

метод Безье

 p = (1-t)^3 *P0 + 3*t*(1-t)^2*P1 + 3*t^2*(1-t)*P2 + t^3*P3

для кубиков и

 p = (1-t)^2 *P0 + 2*(1-t)*t*P1 + t*t*P2

для квадратичных.

t обычно находится на 0-1, но это не существенно - на самом деле кривые простираются до бесконечности. P0, P1, etc управление точки. Кривая проходит через две конечные точки, но обычно не через другие точки.

5

  • Если вы просто хотите, чтобы отобразить кривую Безье, вы можете использовать что-то вроде PolyBezier для Windows.

  • Если вы хотите реализовать процедуру самостоятельно, вы можете найти код линейной интерполяции по всему Интарнетцу.

  • Я считаю библиотеки Boost иметь поддержку для этого. Линейная интерполяция, а не конкретно Безье. Не цитируй меня., однако.

0