как сложность обхода Морриса o (n)?
http://geeksforgeeks.org/?p=6358
Может ли кто-нибудь объяснить, как Morris Traversal имеет временную сложность o(n)? В обходе, всякий раз, когда узел имеет левый дочерний элемент, его копия делается правому дочернему элементу его предшественника. Поэтому в худшем случае предшественник должен быть найден для каждого узла
while(pre->right != NULL && pre->right != current)
pre = pre->right;
что собирается увеличить сложность? Я что-то пропустил?
3 ответов
Он не собирается увеличивать сложность, поскольку алгоритм просто перестраивает дерево только в одном направлении(перестройка занимает только O(n), после чего его только O (n) снова печатает их... но они объединили обе функции в одну и ту же функцию и дали специальное имя для algo, что это...
другой способ взглянуть на это-узнать, сколько раз узел дерева будет пройден. Поскольку он постоянен (3 раза для двоичного дерева). Мы смотрим на O (n).
оригинальный документ для Morris traversal является обход бинарных деревьев просто и дешево. Он утверждает, что временная сложность O( n) в разделе введения:
Это также эффективно, принимая время, пропорциональное количеству узлов в дереве и не требующее ни стека времени выполнения, ни битов флага в узлах.
Полная статья должна иметь анализ сложности времени. Но полная бумага не может быть доступна для бесплатный.
Моррис Traversal方法遍历二叉树(非递归,不用栈,О(1)空间) есть ли какой-то анализ. Она представляет собой перевод соответствующей части:
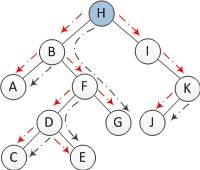
двоичное дерево n-узлов имеет N-1 ребер. В Morris traversal один край посещается не более 2 раз. Один визит для определения местоположения узла. Один визит предназначен для поиска предшественника некоторого узла. В следующем двоичном дереве Красная пунктирная линия предназначена для поиска узла. Черная пунктирная линия для поиска предшественника узел.