Как создать радиальный кластер, как в следующем примере кода в Python?
Я нашел несколько примеров того, как создать эти точные иерархии (по крайней мере, я считаю, что они есть), как здесь stackoverflow.com/questions/2982929/ которые отлично работают и почти выполняют то, что я ищу.
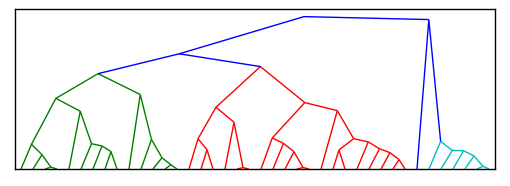
[EDIT] вот упрощенная версия Павел's код, который теперь должен быть проще для кого-то, чтобы помочь получить это в радиальном кластере вместо этого текущего кластера форма
import scipy
import pylab
import scipy.cluster.hierarchy as sch
def fix_verts(ax, orient=1):
for coll in ax.collections:
for pth in coll.get_paths():
vert = pth.vertices
vert[1:3,orient] = scipy.average(vert[1:3,orient])
# Generate random features and distance matrix.
x = scipy.rand(40)
D = scipy.zeros([40,40])
for i in range(40):
for j in range(40):
D[i,j] = abs(x[i] - x[j])
fig = pylab.figure(figsize=(8,8))
# Compute and plot the dendrogram.
ax2 = fig.add_axes([0.3,0.71,0.6,0.2])
Y = sch.linkage(D, method='single')
Z2 = sch.dendrogram(Y)
ax2.set_xticks([])
ax2.set_yticks([])
fix_verts(ax2,0)
fig.savefig('test.png')
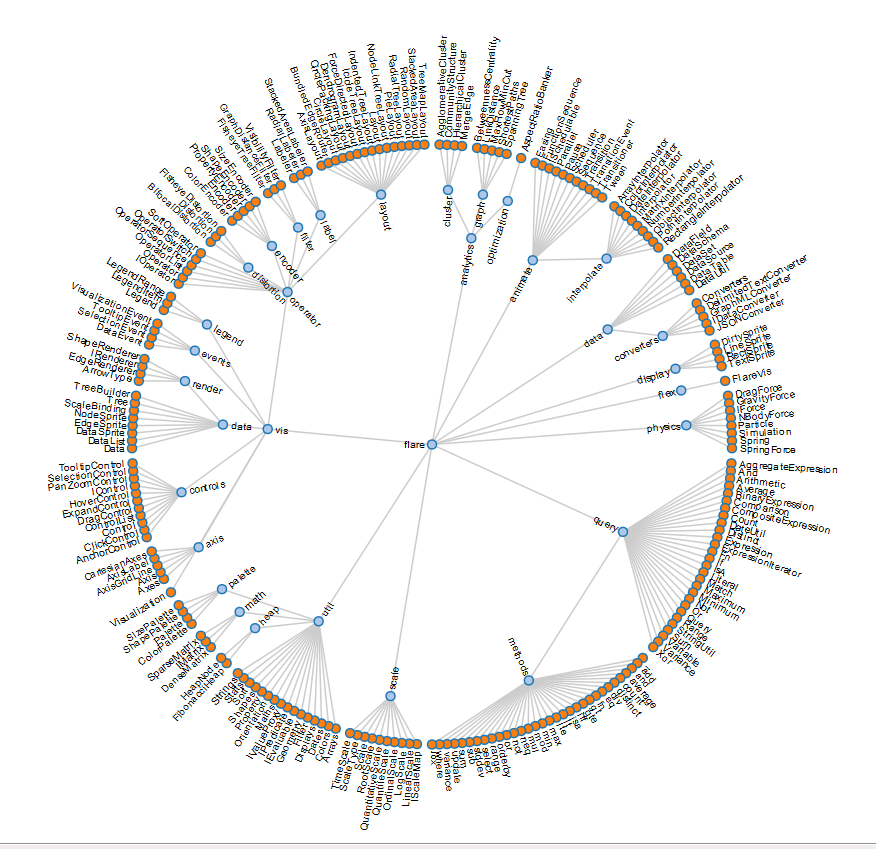
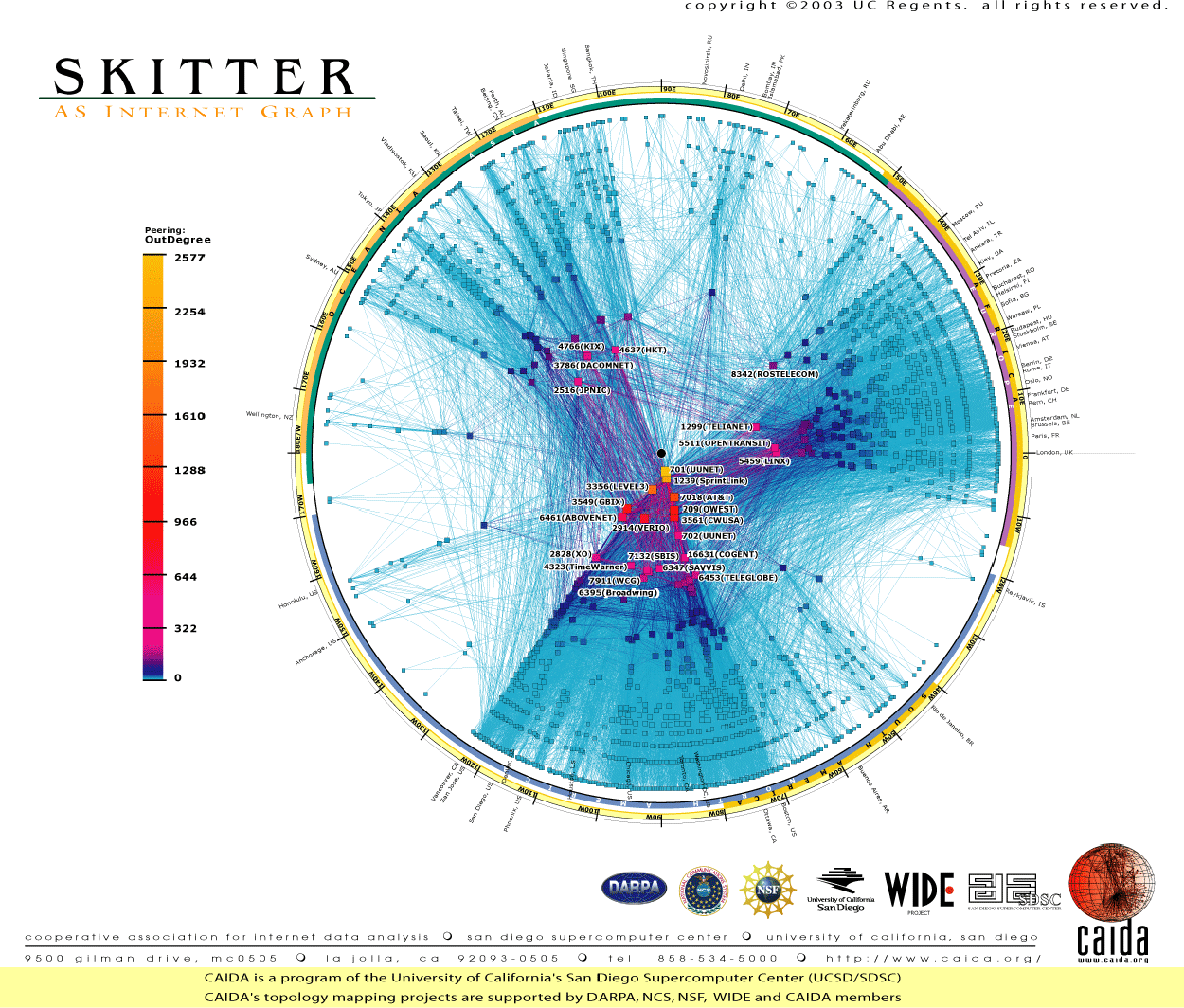
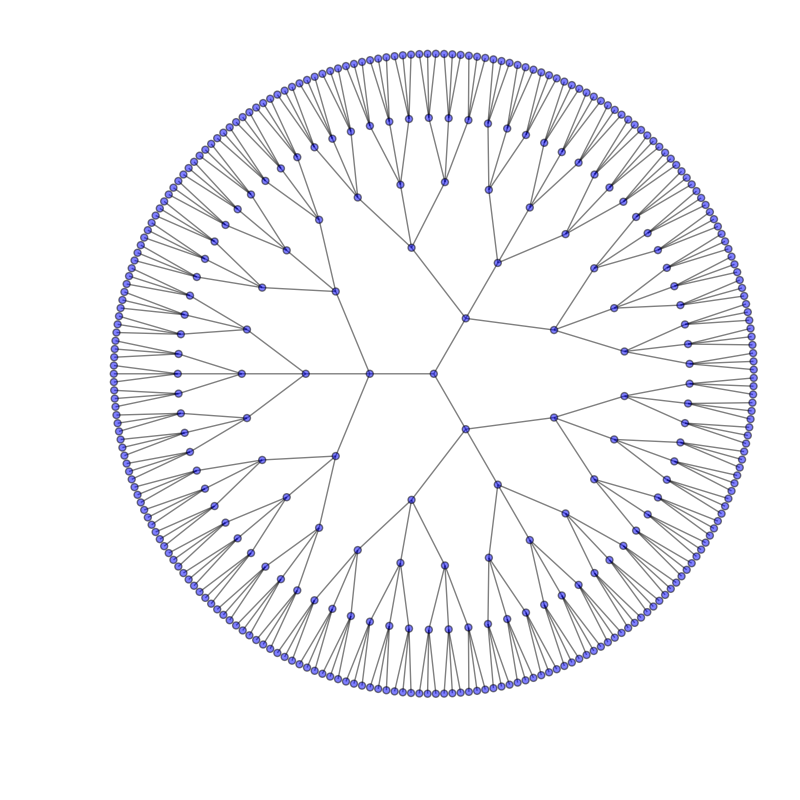
но вместо древовидной структуры мне нужен радиальный кластер, как показано на следующих диаграммах.
3 ответов
Я изучил этот вопрос немного больше, и теперь, кажется, лучше всего создать новую функцию для построенияradial cluster непосредственно с linkage output (вместо взлома построенного). В конце концов я могу что-нибудь придумать, но не очень скоро.
Я предполагаю, что ваши данные, естественно, допускают такой вид радиального внедрения. Вы это проверили? Существует ли подходящий метод в linkage для ваших целей?
кажется, что для любого метода linkage вернет структуру двоичного дерева. В ваших примерах у вас есть более общее дерево. Вам нужны дополнительные знания, как консолидировать узлы дерева. Все это лишает смысла саму идею взлома оригинальной дендрограммы.
обновление:
Будет ли этот наивный пример сюжета достаточно разумным для ваших целей? Если это так, я смогу опубликовать очень простой код для его достижения.
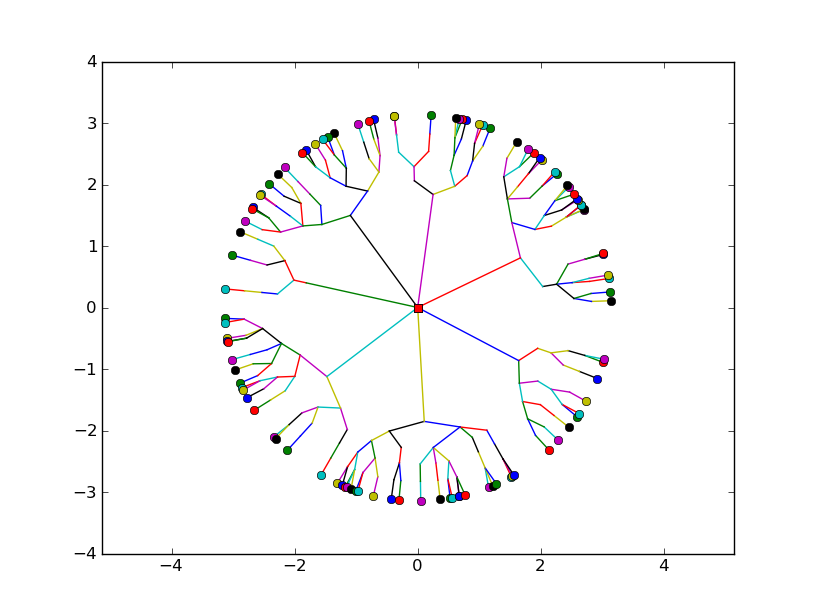
обновление 2:
вот код:
radial_demo.py:
from numpy import r_, ones, pi, sort
from numpy.random import rand
from radial_grouper import tree, pre_order, post_order
from radial_visualizer import simple_link
from pylab import axis, figure, plot, subplot
# ToDo: create proper documentation
def _s(sp, t, o):
subplot(sp)
t.traverse(simple_link, order= o)
axis('equal')
def demo1(n):
p= r_[2* pi* rand(1, n)- pi, ones((1, n))]
t= tree(p)
f= figure()
_s(221, t, pre_order)
_s(222, t, post_order)
t= tree(p, tols= sort(2e0* rand(9)))
_s(223, t, pre_order)
_s(224, t, post_order)
f.show()
# f.savefig('test.png')
# ToDO: implement more demos
if __name__ == '__main__':
demo1(123)
radial_grouper.py:
"""All grouping functionality is collected here."""
from collections import namedtuple
from numpy import r_, arange, argsort, array, ones, pi, where
from numpy import logical_and as land
from radial_support import from_polar
__all__= ['tree', 'pre_order', 'post_order']
Node= namedtuple('Node', 'ndx lnk')
# ToDo: enhance documentation
def _groub_by(p, tol, r):
g, gm, gp= [], [], p- p[0]
while True:
if gp[-1]< 0: break
ndx= where(land(0.<= gp, gp< tol))[0]
if 0< len(ndx):
g.append(ndx)
gm.append(p[ndx].mean())
gp-= tol
return g, array([gm, [r]* len(gm)])
def _leafs(p):
return argsort(p[0])
def _create_leaf_nodes(ndx):
nodes= []
for k in xrange(len(ndx)):
nodes.append(Node(ndx[k], []))
return nodes
def _link_and_create_nodes(_n, n_, cn, groups):
nodes, n0= [], 0
for k in xrange(len(groups)):
nodes.append(Node(n_+ n0, [cn[m] for m in groups[k]]))
n0+= 1
return n_, n_+ n0, nodes
def _process_level(nodes, polar, p, tol, scale, _n, n_):
groups, p= _groub_by(p, tol, scale* polar[1, _n])
_n, n_, nodes= _link_and_create_nodes(_n, n_, nodes, groups)
polar[:, _n: n_]= p
return nodes, polar, _n, n_
def _create_tree(p, r0, scale, tols):
if None is tols:
tols= .3* pi/ 2** arange(5)[::-1]
_n, n_= 0, p.shape[1]
polar= ones((2, (len(tols)+ 2)* n_))
polar[0, :n_], polar[1, :n_]= p[0], r0
# leafs
nodes= _create_leaf_nodes(_leafs(p))
nodes, polar, _n, n_= _process_level(
nodes, polar, polar[0, _leafs(p)], tols[0], scale, _n, n_)
# links
for tol in tols[1:]:
nodes, polar, _n, n_= _process_level(
nodes, polar, polar[0, _n: n_], tol, scale, _n, n_)
# root
polar[:, n_]= [0., 0.]
return Node(n_, nodes), polar[:, :n_+ 1]
def _simplify(self):
# ToDo: combine single linkages
return self._root
def _call(self, node0, node1, f, level):
f(self, [node0.ndx, node1.ndx], level)
def pre_order(self, node0, f, level= 0):
for node1 in node0.lnk:
_call(self, node0, node1, f, level)
pre_order(self, node1, f, level+ 1)
def post_order(self, node0, f, level= 0):
for node1 in node0.lnk:
post_order(self, node1, f, level+ 1)
_call(self, node0, node1, f, level)
class tree(object):
def __init__(self, p, r0= pi, scale= .9, tols= None):
self._n= p.shape[1]
self._root, self._p= _create_tree(p, r0, scale, tols)
def traverse(self, f, order= pre_order, cs= 'Cartesian'):
self.points= self._p
if cs is 'Cartesian':
self.points= from_polar(self._p)
order(self, self._root, f, 0)
return self
def simplify(self):
self._root= _simplify(self)
return self
def is_root(self, ndx):
return ndx== self._p.shape[1]- 1
def is_leaf(self, ndx):
return ndx< self._n
if __name__ == '__main__':
# ToDO: add tests
from numpy import r_, round
from numpy.random import rand
from pylab import plot, show
def _l(t, n, l):
# print round(a, 3), n, l, t.is_root(n[0]), t.is_leaf(n[1])
plot(t.points[0, n], t.points[1, n])
if 0== l:
plot(t.points[0, n[0]], t.points[1, n[0]], 's')
if t.is_leaf(n[1]):
plot(t.points[0, n[1]], t.points[1, n[1]], 'o')
n= 123
p= r_[2* pi* rand(1, n)- pi, ones((1, n))]
t= tree(p).simplify().traverse(_l)
# t= tree(p).traverse(_l, cs= 'Polar')
show()
# print
# t.traverse(_l, post_order, cs= 'Polar')
radial_support.py:
"""All supporting functionality is collected here."""
from numpy import r_, arctan2, cos, sin
from numpy import atleast_2d as a2d
# ToDo: create proper documentation strings
def _a(a0, a1):
return r_[a2d(a0), a2d(a1)]
def from_polar(p):
"""(theta, radius) to (x, y)."""
return _a(cos(p[0])* p[1], sin(p[0])* p[1])
def to_polar(c):
"""(x, y) to (theta, radius)."""
return _a(arctan2(c[1], c[0]), (c** 2).sum(0)** .5)
def d_to_polar(D):
"""Distance matrix to (theta, radius)."""
# this functionality is to adopt for more general situations
# intended functionality:
# - embedd distance matrix to 2D
# - return that embedding in polar coordinates
pass
if __name__ == '__main__':
from numpy import allclose
from numpy.random import randn
c= randn(2, 5)
assert(allclose(c, from_polar(to_polar(c))))
# ToDO: implement more tests
radial_visualizer.py:
"""All visualization functionality is collected here."""
from pylab import plot
# ToDo: create proper documentation
def simple_link(t, ndx, level):
"""Simple_link is just a minimal example to demonstrate what can be
achieved when it's called from _grouper.tree.traverse for each link.
- t, tree instance
- ndx, a pair of (from, to) indicies
- level, of from, i.e. root is in level 0
"""
plot(t.points[0, ndx], t.points[1, ndx])
if 0== level:
plot(t.points[0, ndx[0]], t.points[1, ndx[0]], 's')
if t.is_leaf(ndx[1]):
plot(t.points[0, ndx[1]], t.points[1, ndx[1]], 'o')
# ToDO: implement more suitable link visualizers
# No doubt, this will the part to burn most of the dev. resources
if __name__ == '__main__':
# ToDO: implement tests
pass
вы можете найти исходный код здесь. Пожалуйста, не стесняйтесь изменять его в любом случае, но, пожалуйста, держите будущие изменения синхронизированы с сутью.
Я верю, что вы можете сделать это с помощью в сочетании с matplotlib. Проверьте следующий пример из networkx фотогалерея:
http://networkx.lanl.gov/examples/drawing/circular_tree.html
В общем networkx имеет ряд действительно хороших методов анализа и построения графиков
я добавил функцию fix_verts что объединяет verticies в основании каждой "U" в древовидную схему.
попробуйте это:
import scipy
import pylab
import scipy.cluster.hierarchy as sch
def fix_verts(ax, orient=1):
for coll in ax.collections:
for pth in coll.get_paths():
vert = pth.vertices
vert[1:3,orient] = scipy.average(vert[1:3,orient])
# Generate random features and distance matrix.
x = scipy.rand(40)
D = scipy.zeros([40,40])
for i in range(40):
for j in range(40):
D[i,j] = abs(x[i] - x[j])
fig = pylab.figure(figsize=(8,8))
# Compute and plot first dendrogram.
ax1 = fig.add_axes([0.09,0.1,0.2,0.6])
Y = sch.linkage(D, method='centroid')
Z1 = sch.dendrogram(Y, orientation='right')
ax1.set_xticks([])
ax1.set_yticks([])
# Compute and plot second dendrogram.
ax2 = fig.add_axes([0.3,0.71,0.6,0.2])
Y = sch.linkage(D, method='single')
Z2 = sch.dendrogram(Y)
ax2.set_xticks([])
ax2.set_yticks([])
# Plot distance matrix.
axmatrix = fig.add_axes([0.3,0.1,0.6,0.6])
idx1 = Z1['leaves']
idx2 = Z2['leaves']
D = D[idx1,:]
D = D[:,idx2]
im = axmatrix.matshow(D, aspect='auto', origin='lower', cmap=pylab.cm.YlGnBu)
axmatrix.set_xticks([])
fix_verts(ax1,1)
fix_verts(ax2,0)
fig.savefig('test.png')
результат таков:
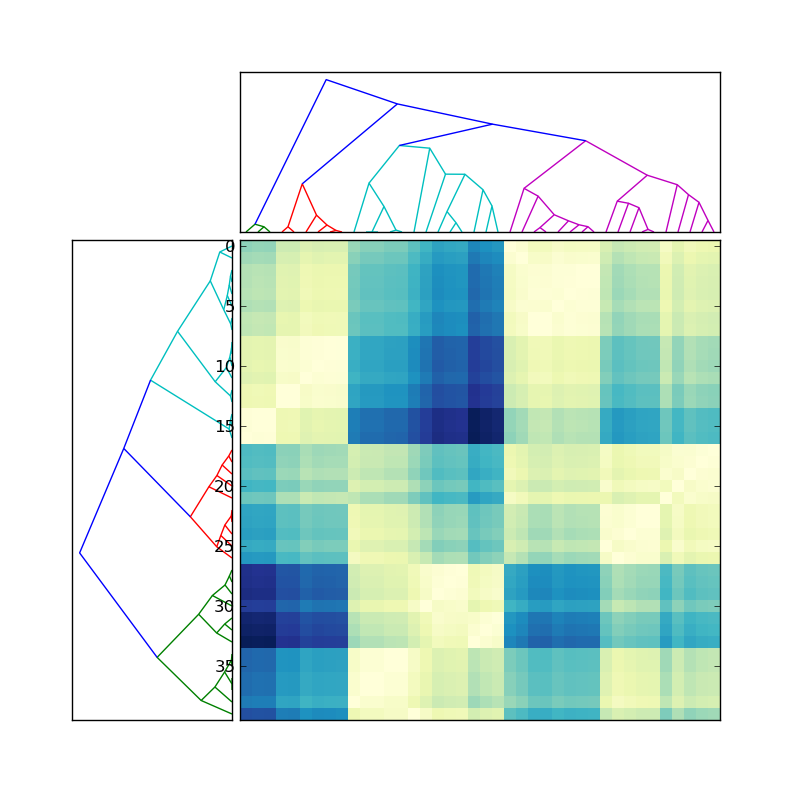
Я надеюсь, что это то, что вы были после.
