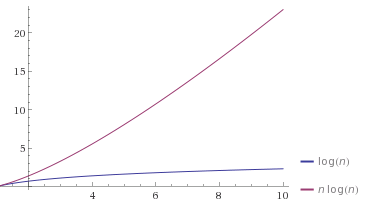
Как вы визуализируете разницу между O(log n) и O (N log n)?
двоичный поиск имеет среднюю производительность case как O(log n) и быстрая сортировка с O(n log n) is O(n log n) совпадает с O(n) + O (log n)
5 ответов
представьте себе базу данных с каждым человеком в мире. Это 6,7 миллиарда записей. O (log n) - это поиск в индексированном столбце (например, первичный ключ). O (n log n) возвращает все население в отсортированном порядке в неиндексированном столбце.
- O (log n) было закончено до того, как вы закончили читать первое слово этого предложения.
- O (N log n) все еще вычисляется...
другой способ представить себе это:
log n пропорционально к числу цифр в n.
n log n в N раз больше.
попробуйте написать число 1000 один раз против написания его тысячу раз. Первый занимает время O(log n), второй-O (N log n).
теперь попробуйте еще раз с 6700000000. Написать его один раз-все равно тривиально. Теперь попробуйте написать его 6,7 миллиарда раз. Даже если бы ты мог писать ее раз в секунду, ты был бы мертв еще до того, как закончил.
нет, O(n log n) = O(n) * O(log n)
в математике, когда у вас есть выражение (т. е. e=mc^2), если нет оператора, то вы умножаете.
обычно способ визуализации O (N log n) - "сделать что-то, что занимает log n расчеты n раза."
если у вас был алгоритм, который сначала перебирал список, а затем выполнял двоичный поиск этого списка (который был бы N + log N) вы can выразите это просто как O(n) потому что n гномов log n для больших значений n
A (log n) участок увеличивается, но вогнут вниз, что означает:
- он увеличивается, когда n становится больше
- Это
зависит от того, склонны ли вы визуализировать n как имеющее конкретное значение.
если вы склонны визуализировать n как имеющие конкретное значение, так и единицы f(n) время или инструкции, то O(log n) is n раза быстрее, чем O(n log n) для данной задачи размера n. Для памяти или единиц пространства, то O(log n) is n раз меньше для данной задачи в размере n. В этом случае, вы хотите обратить внимание на Йодомарин от f(n) для некоторых известных n. Вы визуализируете ответы на вопросы о том, сколько времени что-то займет или сколько памяти будет потреблять эта операция.
если вы склонны визуализировать n в качестве параметра, имеющего любое значение, тогда O(log n) is n раз более масштабируемым. O(log n) может завершить n раз больше задач размера n. В этом случае, вы ориентированы на домене f(n). Вы визуализируете ответы на вопросы о том, насколько велики n может получить, или сколько экземпляров f(n) вы можете работать параллельно.
ни одна перспектива не лучше другой. Первые можно использовать для сравнения подходов к решению конкретной задачи. Последнее может быть использовано для сравнения практических ограничений данных подходов.