Как вычислить контрольные точки кривой Безье, которые избегают объектов?
в частности, я работаю в canvas с javascript.
в основном, у меня есть объекты, которые имеют границы, которые я хочу избежать, но все еще окружают кривой Безье. Однако я даже не уверен, с чего начать писать алгоритм, который будет перемещать контрольные точки, чтобы избежать столкновения.
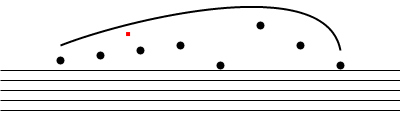
проблема в изображении ниже, даже если вы не знакомы с нотной записью, проблема все равно должна быть довольно ясной. Точки кривой-красные точки!--1-->

кроме того, у меня есть доступ к ограничивающим коробкам каждой ноты, которая включает стержень.

поэтому, естественно, столкновения должны быть обнаружены между ограничивающими рамками и кривыми (некоторое направление здесь было бы хорошо, но я просматривал и вижу, что есть приличное количество информации об этом). Но что происходит после обнаружения столкновений? Что должно произойти, чтобы вычислить местоположения контрольных точек, чтобы сделать что-то похожее на:--1-->

2 ответов
подход Безье
первоначально вопрос является широким - возможно, даже широким, поскольку существует множество различных сценариев, которые необходимо учитывать, чтобы сделать "одно решение, которое подходит для всех". Это целый проект сам по себе. Для этого я представлю основа на решение, которое можно развивать - это не полное решение (но близко к одному..). В конце я добавил несколько предложений по дополнениям.
в основные шаги для этого решения:
сгруппируйте заметки в две группы, левую и правую части.
контрольные точки затем основаны на наибольшем угле от первой (конечной) точки и расстоянии до любой другой заметки в этой группе и последней конечной точки до любой точки во второй группе.
полученные углы из двух групп затем удваиваются (максимум 90°) и используются в качестве основы для расчета контрольных точек (в основном вращение точки). Расстояние может быть дополнительно обрезано с помощью значения натяжения.
угол, удвоение, расстояние, натяжение и отступы смещение позволит для тонкой настройки, чтобы получить лучший результат более всех. Могут быть особые случаи, которые нуждаются в дополнительных условных проверках, но это не относится к сфере охвата (это не будет полным готовым к ключу решением, но обеспечит хорошую основу для дальнейшей работы).
несколько снимков из процесс:
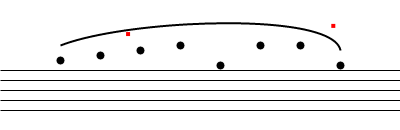
основной код в Примере разделен на два раздела, два цикла, которые анализируют каждую половину, чтобы найти максимальный угол, а также расстояние. Это может быть объединено в один цикл и иметь второй итератор для перехода справа на середину в дополнение к тому, который идет слева на середину, но для простоты и лучшего понимания того, что происходит, я разделил их на два цикла (и ввел ошибку во второй половине-просто знать. Оставлю это как упражнение):
var dist1 = 0, // final distance and angles for the control points
dist2 = 0,
a1 = 0,
a2 = 0;
// get min angle from the half first points
for(i = 2; i < len * 0.5 - 2; i += 2) {
var dx = notes[i ] - notes[0], // diff between end point and
dy = notes[i+1] - notes[1], // current point.
dist = Math.sqrt(dx*dx + dy*dy), // get distance
a = Math.atan2(dy, dx); // get angle
if (a < a1) { // if less (neg) then update finals
a1 = a;
dist1 = dist;
}
}
if (a1 < -0.5 * Math.PI) a1 = -0.5 * Math.PI; // limit to 90 deg.
и то же самое со второй половиной, но здесь мы переворачиваем углы, поэтому их легче обрабатывать, сравнивая текущую точку с конечной точкой вместо конечной точки по сравнению с текущей точкой. После того, как петля сделана, мы переворачиваем ее на 180°:
// get min angle from the half last points
for(i = len * 0.5; i < len - 2; i += 2) {
var dx = notes[len-2] - notes[i],
dy = notes[len-1] - notes[i+1],
dist = Math.sqrt(dx*dx + dy*dy),
a = Math.atan2(dy, dx);
if (a > a2) {
a2 = a;
if (dist2 < dist) dist2 = dist; //bug here*
}
}
a2 -= Math.PI; // flip 180 deg.
if (a2 > -0.5 * Math.PI) a2 = -0.5 * Math.PI; // limit to 90 deg.
(ошибка заключается в том, что самое длинное расстояние используется, даже если более короткая точка расстояния имеет больший угол - я позволю ему быть сейчас, как это подразумевается в качестве примера. Это может быть исправлено путем реверса итерации.).
отношение, которое я нашел, работает хорошо, это разница в углах между полом и точкой два раза:
var da1 = Math.abs(a1); // get angle diff
var da2 = a2 < 0 ? Math.PI + a2 : Math.abs(a2);
a1 -= da1*2; // double the diff
a2 += da2*2;
теперь мы можем просто рассчитать контрольные точки и использовать значение напряжения для точной настройки результата:
var t = 0.8, // tension
cp1x = notes[0] + dist1 * t * Math.cos(a1),
cp1y = notes[1] + dist1 * t * Math.sin(a1),
cp2x = notes[len-2] + dist2 * t * Math.cos(a2),
cp2y = notes[len-1] + dist2 * t * Math.sin(a2);
и вуаля:
ctx.moveTo(notes[0], notes[1]);
ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, notes[len-2], notes[len-1]);
ctx.stroke();
добавление эффекта сужения
создать кривую более визуально угождая сужать можно добавить просто путем делать следующее вместо этого:
вместо поглаживания пути после добавления первой кривой Безье отрегулируйте контрольные точки с небольшим смещением угла. Затем продолжите путь, добавив еще одну кривую Безье, идущую справа налево, и, наконец, заполните ее (fill() закроет путь неявно):
// first path from left to right
ctx.beginPath();
ctx.moveTo(notes[0], notes[1]); // start point
ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, notes[len-2], notes[len-1]);
// taper going from right to left
var taper = 0.15; // angle offset
cp1x = notes[0] + dist1*t*Math.cos(a1-taper);
cp1y = notes[1] + dist1*t*Math.sin(a1-taper);
cp2x = notes[len-2] + dist2*t*Math.cos(a2+taper);
cp2y = notes[len-1] + dist2*t*Math.sin(a2+taper);
// note the order of the control points
ctx.bezierCurveTo(cp2x, cp2y, cp1x, cp1y, notes[0], notes[1]);
ctx.fill(); // close and fill
конечный результат (с псевдо-нотами-натяжение = 0.7, заполнение = 10)
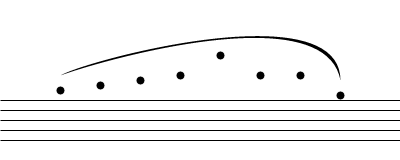
предложения по улучшению:
- если расстояния обеих групп большие или углы крутые, их, вероятно, можно использовать как сумму для уменьшения напряжения (расстояния) или увеличения его (угла).
- фактор доминирования / площади может повлиять на расстояния. Доминирование, указывающее, где самые высокие части смещены (лежит ли он больше в левой или правой стороне, и влияет на напряжение для каждой стороны соответственно). Это может быть / потенциально достаточно само по себе, но должно быть протестировано.
- смещение угла конусности также должно иметь отношение к сумме расстояния. В некоторых случаях линии пересекаются и выглядят не очень хорошо. Сужение может быть заменено ручным подходом, анализирующим точки Безье (ручная реализация) и добавляющим расстояние между исходными точками и точками для возвращаемого пути в зависимости от массива позиция.
надеюсь, что это помогает!
кардинальный сплайн и фильтрационный подход
если вы открыты для использования подхода Безье, то следующее может дать приблизительную кривую над стеблями нот.
такое решение состоит из 4 шагов:
- собирать верхние ноты / стебли
- отфильтровать "провалы" в пути
- отфильтровать точки на том же склоне
- создать кардинальную сплайновую кривую
это прототип решение, поэтому я не тестировал его против каждой возможной комбинации. Но это должно дать вам хорошую отправную точку и основу для продолжения.
первый шаг прост, собирать точки, представляющие верхнюю часть ствола заметки - для демонстрации я использую следующую коллекцию точек, которая слегка представляет изображение, которое у вас есть в сообщении. Они расположены в порядке x, y:
var notes = [60,40, 100,35, 140,30, 180,25, 220,45, 260,25, 300,25, 340,45];
который будет представлен как это:

затем я создал простой многопроходный алгоритм, который отфильтровывает провалы и точки На одном склоне. Шаги в алгоритме следующие:
- хотя есть
anotherPass(true) это будет продолжаться, или пока максимальное количество проходов изначально - точка копируется в другой массив до тех пор, пока
skipфлаг не установлен - затем он будет сравнивать текущую точку с next, чтобы увидеть, имеет ли она вниз-склон
- если это так, он будет сравнивать следующую точку со следующей и посмотреть, имеет ли она уклон вверх
- если это считается купанием и
skipфлаг установлен так, что следующая точка (текущая средняя точка) не будет скопирована - следующий фильтр будет сравнивать наклон между текущей и следующей точкой, а также следующей точкой и следующим.
- если они одинаковы
skipфлаг установлен. - если он должен был назначить
skipфлаг будет также установитьanotherPassфлаг. - если нет точек, где фильтруется (или МАКС проходит не достигается) цикл закончится
основная функция выглядит следующим образом:
while(anotherPass && max) {
skip = anotherPass = false;
for(i = 0; i < notes.length - 2; i += 2) {
if (!skip) curve.push(notes[i], notes[i+1]);
skip = false;
// if this to next points goes downward
// AND the next and the following up we have a dip
if (notes[i+3] >= notes[i+1] && notes[i+5] <= notes[i+3]) {
skip = anotherPass = true;
}
// if slope from this to next point =
// slope from next and following skip
else if (notes[i+2] - notes[i] === notes[i+4] - notes[i+2] &&
notes[i+3] - notes[i+1] === notes[i+5] - notes[i+3]) {
skip = anotherPass = true;
}
}
curve.push(notes[notes.length-2], notes[notes.length-1]);
max--;
if (anotherPass && max) {
notes = curve;
curve = [];
}
}
результат первого прохода будет после смещения всех точек на оси y-обратите внимание, что примечание погружения игнорируется:

после выполнения всех необходимых проходов конечный массив точек будет представлен как это:

единственный оставшийся шаг-сгладить кривую. Для этого я использовал свою собственную реализацию кардинального сплайна (лицензированного под MIT и может быть найти здесь), который принимает массив с точками x, y и сглаживает его, добавляя интерполированные точки на основе значения напряжения.
он не будет генерировать идеальную кривую, но результат от этого будет быть:
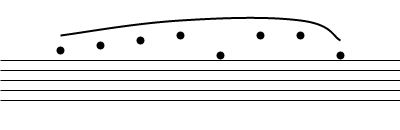
есть способы улучшить визуальный результат, который я не рассматривал, но я оставлю его вам, чтобы сделать это, если вы чувствуете, что это необходимо. Среди них могли быть:
- найдите центр точек и увеличьте смещение в зависимости от угла, чтобы он больше дуг вверху
- конечные точки сглаженной кривой иногда слегка завиваются - это можно исправить, добавив начальная точка прямо под первой точкой, а также в конце. Это заставит кривую иметь более красивый старт / конец.
- вы можете нарисовать двойную кривую, чтобы сделать эффект конусности (тонкое начало/конец, толще посередине), используя первую точку в этом списке на другом массиве, но с очень небольшим смещением в верхней части дуги, а затем отобразить ее сверху.
алгоритм был создан ad-hook для этого ответа, поэтому он, очевидно, не проверен должным образом. Там может будьте особыми случаями и комбинацией, но я думаю, что это хорошее начало.
известные недостатки:
- предполагается, что расстояние между каждым стержнем одинаково для обнаружения наклона. Это необходимо заменить факторным сравнением в случае, если расстояние варьируется внутри группы.
- он сравнивает наклон с точными значениями, которые могут потерпеть неудачу, если используются значения с плавающей запятой. Сравните с epsilon / tolerance
