Как вычислить вероятность значения, заданного списком образцов из дистрибутива в Python?
Не уверен, что это относится к статистике, но я пытаюсь использовать Python для достижения этого. У меня, по сути, есть список целых чисел:
data = [300,244,543,1011,300,125,300 ... ]
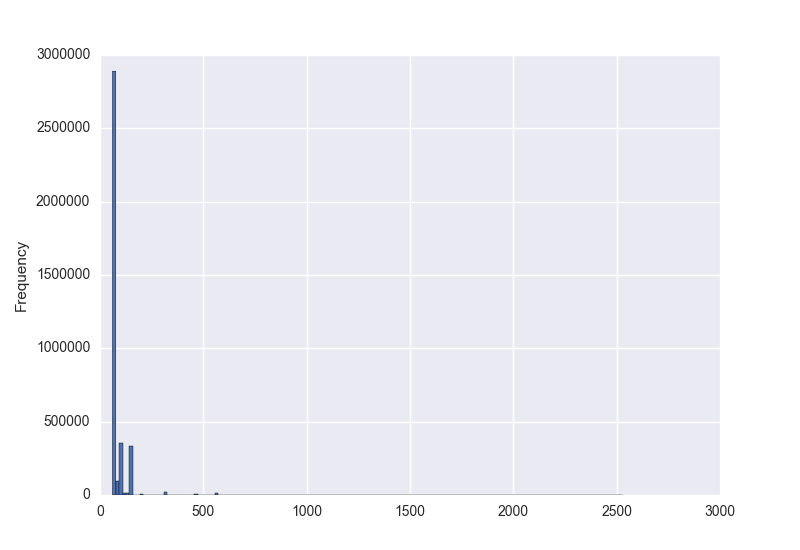
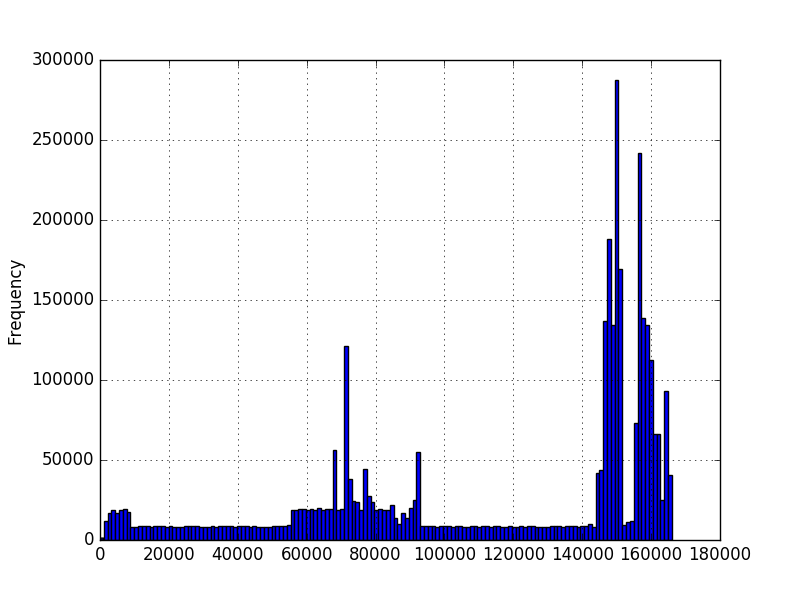
и я хотел бы знать вероятность возникновения значения с учетом этих данных. Я построил гистограммы данных с помощью matplotlib и получил их:
на первом графике числа представляют количество символов в последовательность. На втором графике это измеренное количество времени в миллисекундах. Минимум больше нуля, но не обязательно есть максимум. Графики были созданы с использованием миллионов примеров, но я не уверен, что могу сделать какие-либо другие предположения о распределении. Я хочу знать вероятность нового значения, учитывая, что у меня есть несколько миллионов примеров значений. На первом графике у меня несколько миллионов последовательностей разной длины. Хотелось бы знать вероятность длины 200, например.
Я знаю, что для непрерывного распределения вероятность любой точке должна быть равна нулю, но учитывая поток новых значений, мне нужно быть в состоянии сказать, насколько вероятно каждое значение. Я просмотрел некоторые функции плотности вероятности numpy/scipy, но я не уверен, какой выбрать или как запросить новые значения, как только я запускаю что-то вроде scipy.статистика.норма.pdf (data). Похоже, что разные функции плотности вероятности будут соответствовать данным по-разному. Учитывая форму гистограмм, я не уверен, как решить, что использовать.
3 ответов
поскольку у вас, похоже, нет конкретного распределения, но у вас может быть много образцов данных, я предлагаю использовать непараметрический метод оценки плотности. Один из типов данных, которые вы описываете (время в МС), явно непрерывен, а одним из методов непараметрической оценки функции плотности вероятности (PDF) для непрерывных случайных величин является гистограмма, о которой вы уже упоминали. Однако, как вы увидите ниже, оценка плотности ядра (KDE) может быть лучше. Второй тип данных, который вы описываете (количество символов в последовательности), является дискретным. Здесь оценка плотности ядра также может быть полезна и может рассматриваться как метод сглаживания для ситуаций, когда у вас нет достаточного количества выборок для всех значений дискретной переменной.
Оценка Плотности
в приведенном ниже примере показано, как сначала генерировать образцы данных из смеси 2 гауссовых распределений, а затем применять плотность ядра оценка для нахождения функции плотности вероятности:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
from sklearn.neighbors import KernelDensity
# Generate random samples from a mixture of 2 Gaussians
# with modes at 5 and 10
data = np.concatenate((5 + np.random.randn(10, 1),
10 + np.random.randn(30, 1)))
# Plot the true distribution
x = np.linspace(0, 16, 1000)[:, np.newaxis]
norm_vals = mlab.normpdf(x, 5, 1) * 0.25 + mlab.normpdf(x, 10, 1) * 0.75
plt.plot(x, norm_vals)
# Plot the data using a normalized histogram
plt.hist(data, 50, normed=True)
# Do kernel density estimation
kd = KernelDensity(kernel='gaussian', bandwidth=0.75).fit(data)
# Plot the estimated densty
kd_vals = np.exp(kd.score_samples(x))
plt.plot(x, kd_vals)
# Show the plots
plt.show()
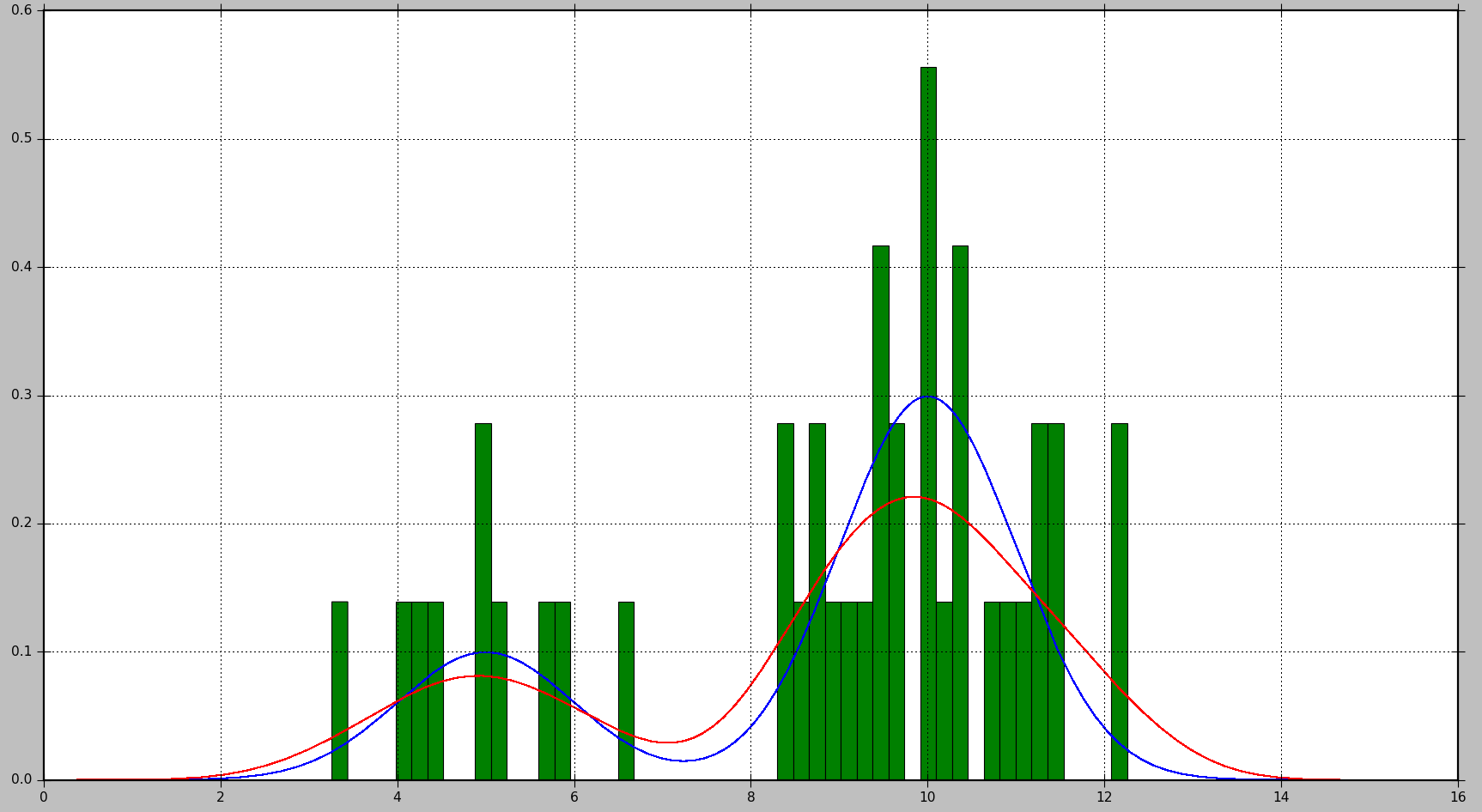
это приведет к следующему графику, где истинное распределение показано синим цветом, гистограмма показана зеленым цветом, а PDF, оцененный с помощью KDE, показан красным цветом:
как вы можете видеть, в этой ситуации PDF, аппроксимированный гистограммой, не очень полезен, в то время как KDE дает гораздо лучшую оценку. Однако при большем числе выборок данных и правильный выбор размера Бина, гистограммы также может дать хорошую оценку.
параметры, которые вы можете настроить в случае KDE являются ядро и ширина полосы. Вы можете думать о ядре как о строительном блоке для оцененного PDF, и несколько функций ядра доступны в Scikit Learn: гауссова, тофата, епанечникова, экспоненциальная, линейная, косинусная. Изменение полосы пропускания позволяет настроить компромисс смещения-дисперсии. Большая пропускная способность приведет к увеличению смещения, что хорошо, если у вас меньше выборок данных. Меньшая пропускная способность увеличит дисперсию (в оценку будет включено меньше выборок), но даст лучшую оценку, когда будет доступно больше выборок.
Расчет Вероятности
для PDF вероятность получается путем вычисления интеграла по диапазону значений. Как вы заметили, это приведет к вероятности 0 для определенного значения.
Scikit Learn не кажется иметь встроенную функцию для вычисления вероятности. Тем не менее, легко оценить Интеграл PDF в диапазоне. Мы можем сделать это, оценив PDF несколько раз в пределах диапазона и суммируя полученные значения, умноженные на размер шага между каждой точкой оценки. В приведенном ниже примере N образцы получены с шагом step.
# Get probability for range of values
start = 5 # Start of the range
end = 6 # End of the range
N = 100 # Number of evaluation points
step = (end - start) / (N - 1) # Step size
x = np.linspace(start, end, N)[:, np.newaxis] # Generate values in the range
kd_vals = np.exp(kd.score_samples(x)) # Get PDF values for each x
probability = np.sum(kd_vals * step) # Approximate the integral of the PDF
print(probability)
обратите внимание:kd.score_samples генерирует лог-вероятность выборки данных. Следовательно,np.exp нужен для получения вероятность.
то же вычисление может быть выполнено с использованием встроенных методов интеграции SciPy, что даст немного более точный результат:
from scipy.integrate import quad
probability = quad(lambda x: np.exp(kd.score_samples(x)), start, end)[0]
например, для одного запуска первый метод рассчитал вероятность как 0.0859024655305, в то время как второй метод производил 0.0850974209996139.
хорошо, я предлагаю это в качестве отправной точки, но оценка плотности-очень широкая тема. Для вашего случая, связанного с количеством символов в последовательности, мы можем смоделировать это с прямой частотной точки зрения, используя эмпирическая вероятность. Здесь вероятность по существу является обобщением понятия процента. В нашей модели пространство выборки дискретно и представляет собой все положительные целые числа. Ну, тогда вы просто подсчитываете вхождения и делите на общее число событий, чтобы получить вашу оценку вероятности. Везде, где у нас есть нулевые наблюдения, наша оценка вероятности равна нулю.
>>> samples = [1,1,2,3,2,2,7,8,3,4,1,1,2,6,5,4,8,9,4,3]
>>> from collections import Counter
>>> counts = Counter(samples)
>>> counts
Counter({1: 4, 2: 4, 3: 3, 4: 3, 8: 2, 5: 1, 6: 1, 7: 1, 9: 1})
>>> total = sum(counts.values())
>>> total
20
>>> probability_mass = {k:v/total for k,v in counts.items()}
>>> probability_mass
{1: 0.2, 2: 0.2, 3: 0.15, 4: 0.15, 5: 0.05, 6: 0.05, 7: 0.05, 8: 0.1, 9: 0.05}
>>> probability_mass.get(2,0)
0.2
>>> probability_mass.get(12,0)
0
Теперь, для ваших данных синхронизации, более естественно моделировать это как непрерывное распределение. Вместо использования параметрического подхода, когда предполагается, что данные имеют некоторое распределение, а затем соответствуют этому распределению, следует использовать непараметрический подход. Один простой способ-использовать плотность ядра оценка. Вы можете просто думать об этом как способ сглаживания гистограммы, чтобы дать вам непрерывную функцию плотности вероятности. Имеется несколько библиотек. Пожалуй, самый простой для данных однофакторного является составляющей это:
>>> import scipy.stats
>>> kde = scipy.stats.gaussian_kde(samples)
>>> kde.pdf(2)
array([ 0.15086911])
чтобы получить вероятность наблюдения в некотором интервале:
>>> kde.integrate_box_1d(1,2)
0.13855869478828692
вот одно из возможных решений. Подсчитать количество вхождений каждого значения в исходном списке. Будущая вероятность для данного значения - это его прошлая частота встречаемости, которая является просто # прошлых вхождений, разделенных на длину исходного списка. В Python это очень просто:
x-заданный список значений
from collections import Counter
c = Counter(x)
def probability(a):
# returns the probability of a given number a
return float(c[a]) / len(x)