Как выполнить ранговый отбор в генетическом алгоритме?

то, что вы описали, просто выбор колеса рулетки.в выборе колеса рулетки:

• родители выбираются в соответствии с их пригодностью
• чем лучше хромосомы, тем больше шансов быть выбранными у них есть.

представьте себе колесо рулетки, где все хромосомы в популяции размещены, каждая хромосома имеет свое место большой, соответственно, его функции, как в следующем картина.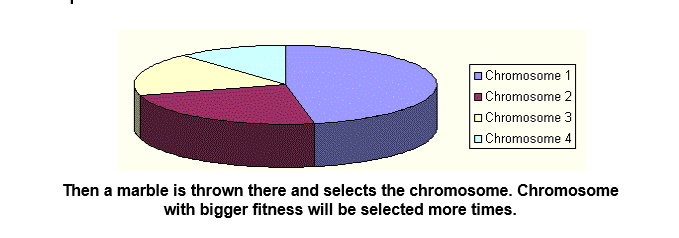
Этот выбор будет иметь проблемы, когда тонкости отличаются очень сильно. Выдающиеся личности привнесут предвзятость в начале поиска, что может привести к преждевременной конвергенции и потере разнообразия.
Например:

если начальная популяция содержит один или два очень подходящих, но не лучших индивидуумы и остальная часть населения не хороши, тогда эти подходят лица будут быстро доминировать над всем населением и предотвращать население от изучения других потенциально лучших индивидуумов. Такое сильное доминирование приводит к очень высокой потере генетического разнообразия что, безусловно, не выгодно для процесса оптимизации.

но в выборе ранг:

1. ранговый отбор сначала ранжирует популяцию, а затем каждая хромосома получает пригодность от этого рейтинга.

2. хуже будет фитнес-1, вторая 2 и т. д. а лучше всего будет иметь пригодность N (количество хромосом в популяции).

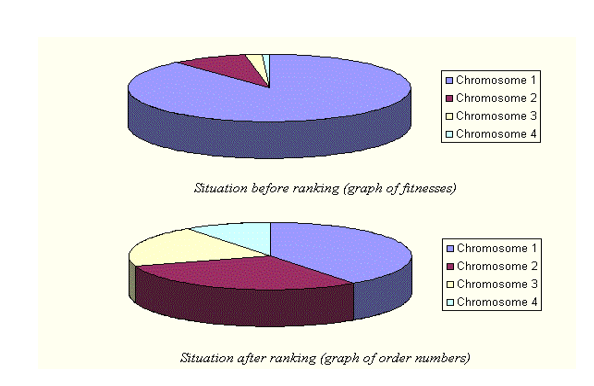
3. после этого все хромосомы имеют шанс быть выбранными.

4. Ранговые схемы выбора могут избежать преждевременной конвергенции.
5. но может быть вычислительно дорогим, потому что он сортирует популяции на основе значения пригодности.
6. но этот метод может привести к замедлению сходимости, потому что лучшие хромосомы не так сильно отличаются от других.

таким образом, процесс будет:

1. сначала отсортируйте значение пригодности населения.

2. тогда, если число популяции равно 10, то дайте вероятность выбора популяции, как 0.1, 0.2, 0.3,...,1.0 .

3. затем вычислить совокупный Фитнес и сделать колесо рулетки.
4. и следующие шаги такие же, как рулетка колесо.

моя реализация выбора ранга в Matlab:

NewFitness=sort(Fitness);
        NewPop=round(rand(PopLength,IndLength));

        for i=1:PopLength
            for j=1:PopLength
                if(NewFitness(i)==Fitness(j))
                    NewPop(i,1:IndLength)=CurrentPop(j,1:IndLength);
                    break;
                end
            end
        end
        CurrentPop=NewPop;

        ProbSelection=zeros(PopLength,1);
        CumProb=zeros(PopLength,1);

        for i=1:PopLength
            ProbSelection(i)=i/PopLength;
            if i==1
                CumProb(i)=ProbSelection(i);
            else
                CumProb(i)=CumProb(i-1)+ProbSelection(i);
            end
        end

        SelectInd=rand(PopLength,1);

        for i=1:PopLength
            flag=0;
            for j=1:PopLength
                if(CumProb(j)<SelectInd(i) && CumProb(j+1)>=SelectInd(i))
                    SelectedPop(i,1:IndLength)=CurrentPop(j+1,1:IndLength);
                    flag=1;
                    break;
                end
            end
            if(flag==0)
                SelectedPop(i,1:IndLength)=CurrentPop(1,1:IndLength);
            end
        end

Примечание: вы также можете увидеть мой вопрос относительно выбора ранга здесь в этом ссылке и мои статьи здесь.

Я также был немного смущен различными источниками о том, как вычисляются вероятности при использовании Выбор Линейного Ранжирования, иногда также называемый "выбор ранга", как упоминается здесь. По крайней мере, я надеюсь, что эти двое имеют в виду одно и то же.

часть, которая была неуловима для меня, - это сумма рангов который, по-видимому, был опущен или, по крайней мере, явно не указан в большинстве источников. Здесь я представляю краткий, но подробный Python пример того, как вычисляется распределение вероятностей (эти хорошие диаграммы вы часто видите).

предполагая, что это некоторые примеры отдельных fintesses: 10, 9, 3, 15, 85, 7.

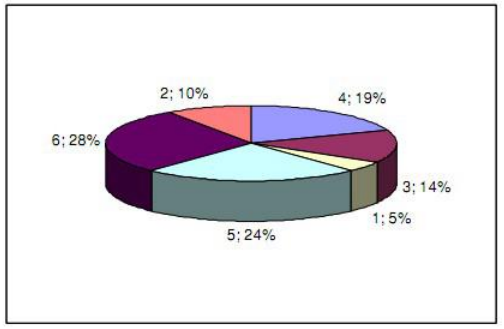
после сортировки назначьте ряды в порядке возрастания: 1st:3, 2-я: 7, 3-й: 9, 4-й: 10, 5-й: 15, 6-я: 85

сумма всех рядах 1+2+3+4+5+6 или используя формулу Гаусса (6+1)*6/2 = 21.

таким образом, мы вычисляем вероятности: 1/21, 2/21, 3/21, 4/21, 5/21, 6/21, которые затем можно выразить в процентах:

обратите внимание, что это не то, что используется в реальных реализаций генетических алгоритмов, только вспомогательный скрипт, чтобы дать вам лучшее представление.

Вы можете вставить этот скрипт:

curl -o ranksel.py https://gist.githubusercontent.com/kburnik/3fe766b65f7f7427d3423d233d02cd39/raw/5c2e569189eca48212c34b3ea8a8328cb8d07ea5/ranksel.py

#!/usr/bin/env python

"""
Assumed name of script: ranksel.py

Sample program to estimate individual's selection probability using the Linear
Ranking Selection algorithm - a selection method in the field of Genetic
Algorithms. This should work with Python 2.7 and 3.5+.

Usage:

./ranksel.py f1 f2 ... fN

Where fK is the scalar fitness of the Kth individual. Any ordering is accepted.

Example:

$ python -u ranksel.py 10 9 3 15 85 7
Rank Fitness Sel.prob.
   1    3.00     4.76%
   2    7.00     9.52%
   3    9.00    14.29%
   4   10.00    19.05%
   5   15.00    23.81%
   6   85.00    28.57%

"""

from __future__ import print_function
import sys

def compute_sel_prob(population_fitness):
  """Computes and generates tuples of (rank, individual_fitness,
     selection_probability) for each individual's fitness, using the Linear
     Ranking Selection algorithm."""
  # Get the number of individuals in the population.
  n = len(population_fitness)

  # Use the gauss formula to get the sum of all ranks (sum of integers 1 to N).
  rank_sum = n * (n + 1) / 2

  # Sort and go through all individual fitnesses; enumerate ranks from 1.
  for rank, ind_fitness in enumerate(sorted(population_fitness), 1):
    yield rank, ind_fitness, float(rank) / rank_sum


if __name__ == "__main__":
  # Read the fitnesses from the command line arguments.
  population_fitness = list(map(float, sys.argv[1:]))

  print ("Rank Fitness Sel.prob.")
  # Iterate through the computed tuples and print the table rows.
  for rank, ind_fitness, sel_prob in compute_sel_prob(population_fitness):
    print("%4d %7.2f %8.2f%%" % (rank, ind_fitness, sel_prob * 100))