Как я могу запрограммировать случайное блуждание в Mathematica?

в плоскости (двумерной) путь может быть представлен последовательностью (n+1) точек (Xo, Yo), (X1, Y1),..., (Xn,Yn) такое, что для любого i (целое число 1 

Pi(vector) = [Xi-X(i-1),Yi-Y(i-1)]

представляющий I-й шаг, является вектором с длиной Pi, а значение изменения направления между векторами Pi и P(i+1) измеряется алгебраически (не знаю как) углом поворота a(i).

Как и любое угловое распределение (изменения направления) характеризуется средний вектор, который принимается симметричным и имеет среднее угловое Φ = o. Подход к этому анализу включает численное моделирование, поскольку алгебраический подход кажется слишком сложным, и я должен использовать псевдослучайный гауссовский генератор для получения непрерывных значений из нормального распределения со средним значением 0 и стандартным отклонением σ (0,1-1,2)радианов для моделирования пути.

поэтому после каждого шага с длиной P (является константой i.е 125 км), значение изменения направления (угол поворота a (i)) определяется псевдослучайным генератором для заданного значения σ, которое является постоянным вдоль пути. А потом делает шаг в следующем направлении, и так далее.

некоторые полезные уравнения:

a(i) ~ n(0,σ)
Θ(i+1) = Θ(i) + a(i)
X(i+1) = Xi + P Cos[Θ(i+1)]
Y(i+1) = Yi + P Sin[Θ(i+1)]

где Θi представляет направление I-го шага. Направление первого шага Θi выбирается случайным образом в соответствии с равномерным угловым распределением псевдослучайным равномерным генератором. Углы поворота записываются от -Pi до Пи

Итак, мой вопрос:

Как я могу взять i.e 12 семейств из 500 ступенчатых путей, каждое из которых характеризуется заданным значением стандартного отклонения σ в диапазоне от 0,1 до 1,2 Радиана, распределения изменений направления между последовательными шагами и построения его в Mathematica? Я ничего не знаю о Mathematica специально, как написать код для этой проблемы.

7
physics plot wolfram-mathematica

3 ответов

после ваших обозначений в вопросе вы используете независимые нормальные приращения для построения угла, а затем используете его в качестве направления для следующего шага размера size.

Block[{size=0.5}, Graphics[
 Line[Accumulate[
   Function[x, size*{Re[x], Im[x]}, Listable][
    Exp[I Accumulate[
       RandomVariate[NormalDistribution[0, Pi/4], 10^3]]]]]]
 ]]

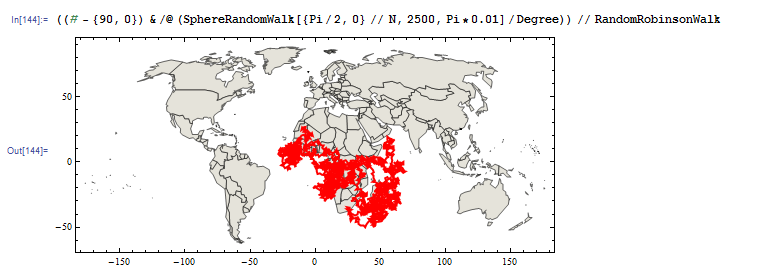
enter image description here

редактировать: это ответ на просьбу г. Ксары визуализировать случайное блуждание по проекции сферы Робинсона. 
RandomRobinsonWalk[coords_List] := 
 Show[CountryData["World", {"Shape", "Robinson"}], 
  Graphics[{Thick, Red, 
    Line[Map[ GeoGridPosition[ GeoPosition[#], "Robinson"][[1]] & , 
      coords]]}], Frame -> True]

генерация случайного блуждания по сфере выполняется следующим образом:

Coordinates[{\[Theta]_, \[Phi]_}, {cosa_, 
    sina_}, \[CapitalDelta]\[Theta]_] := {ArcCos[
    Cos[\[CapitalDelta]\[Theta]] Cos[\[Theta]] - 
     cosa Sin[\[CapitalDelta]\[Theta]] Sin[\[Theta]]], 
   ArcTan[cosa Cos[\[Theta]] Cos[\[Phi]] Sin[\[CapitalDelta]\[Theta]] \
+ Cos[\[CapitalDelta]\[Theta]] Cos[\[Phi]] Sin[\[Theta]] + 
     sina Sin[\[CapitalDelta]\[Theta]] Sin[\[Phi]], (cosa \
Cos[\[Theta]] Sin[\[CapitalDelta]\[Theta]] + 
        Cos[\[CapitalDelta]\[Theta]] Sin[\[Theta]]) Sin[\[Phi]] - 
     Cos[\[Phi]] sina Sin[\[CapitalDelta]\[Theta]]]};

Clear[SphereRandomWalk];
SphereRandomWalk[ipos_, steps_, stepsize_, prec_: MachinePrecision] :=
 FoldList[Function[{up, cossin}, Coordinates[up, cossin, stepsize]], 
  ipos, Function[u, {Re[u], Im[u]}, Listable][
   Exp[I RandomVariate[UniformDistribution[{-Pi, Pi}], steps]]]]

формула чтобы получить следующий {\[Theta], \[Phi} пара была получена следующим образом:

Expand[Simplify[((RotationMatrix[\[Alpha], {Sin[\[Theta]] Sin[\[Phi]],
          Sin[\[Theta]] Cos[\[Phi]], 
         Cos[\[Theta]]}].({Sin[\[Theta]] Sin[\[Phi]], 
          Sin[\[Theta]] Cos[\[Phi]], 
          Cos[\[Theta]]} /. {\[Theta] -> \[Theta] + \[CapitalDelta]\
\[Theta]}))) /. {Conjugate -> Identity} /. {Abs[x_]^2 :> x^2}]]

то есть, выполните вращение фиксированного размера в [тета] , а затем поверните вокруг предыдущего вектора на случайный угол \[Alpha].

использование:

((# - {90, 0}) & /@ (SphereRandomWalk[{Pi/2, 0} // N, 2500, Pi*0.01]/
     Degree)) // RandomRobinsonWalk

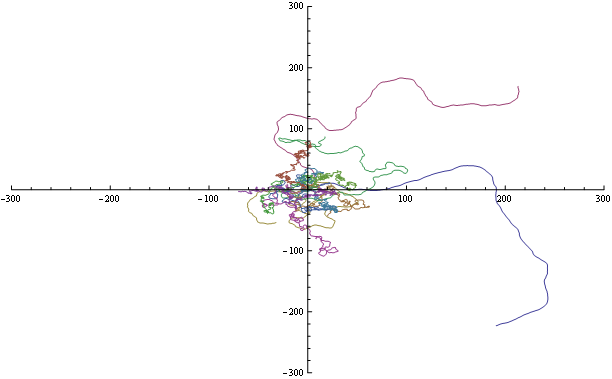
enter image description here

8

ответ Саши-это путь, но, поскольку вы начинаете с ММА, возможно, процедурную программу легче понять.
Обратите внимание, что я не говорю, что это хороший способ делать вещи в ММА. 

P = 1;
For[iter = 1, iter < 13, iter++,
 sigma = iter/10;
 a = RandomVariate[NormalDistribution[0, sigma], 500];
 Clear[theta, x];
 theta[i_] := theta[i] = theta[i - 1] + a[[i]];
 x[i_] := x[i] = x[i - 1] + P {Cos[theta[i]], Sin[theta[i]]};
 theta[0] = RandomReal[{0, 2 Pi}];
 x[0] = {0, 0};
 For[step = 1, step < 500, step++,
  r[iter, step] = x[step];
  ]
 ]
Show@Table[
  ListLinePlot[Table[r[s, i], {i, 500}], PlotStyle -> ColorData[1][s],
    PlotRange -> 300 {{-1, 1}, {-1, 1}}], {s, 1, 12}]

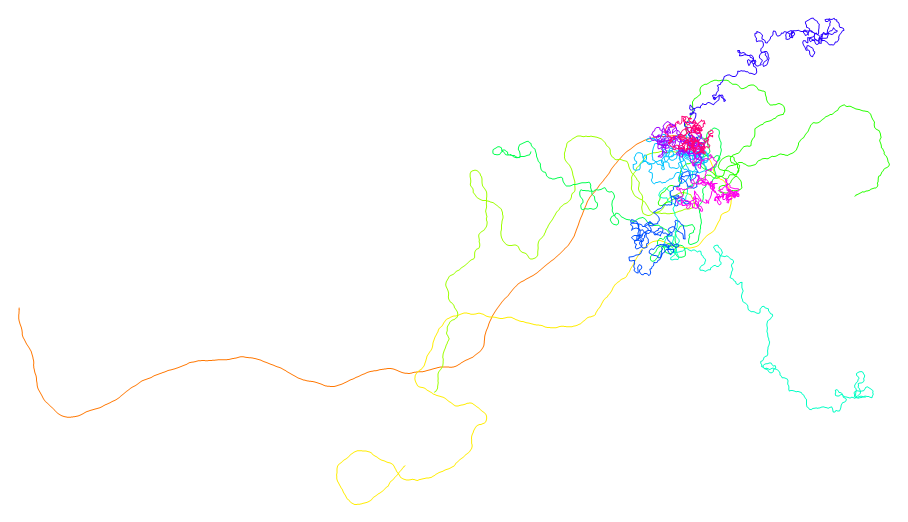
enter image description here

5

следующий код отображает ваши двенадцать семейств в разных цветах, и если вы наведете курсор мыши на строку, вы получите Сигму в подсказке.

Graphics[
 Table[
  {x, y} = {0, 0};
  p = 1;
  \[Theta] = RandomReal[{-\[Pi], \[Pi]}];
  Tooltip[
   {
    Hue[\[Sigma]/1.3],
    Line[
     NestList[(\[Theta] += 
         RandomVariate[NormalDistribution[0, \[Sigma]]]; # + 
         p {Cos[\[Theta]], Sin[\[Theta]]}) &, {x, y}, 500]
     ]
    }, \[Sigma]
   ],
  {\[Sigma], 0.1, 1.2, 0.1}
  ]
 ]

enter image description here

5