Каков наилучший способ выбрать максимальный из списка списков по их последнему элементу?
В Mathematica, Max[] является наиболее эффективной функцией для получения максимального числа в списке чисел, но как найти список с максимальным последним элементом в списке списков? например, 2-d координата с самым большим x часть в серии координат.
моя лучшая попытка -SortBy, но, очевидно, мне не нужна программа для сортировки моего списка, только максимальный, который мне нужен.
6 ответов
возможно:
list = {{4, 3}, {5, 10}, {-2, 1}, {3, 7}}
Reverse /@ Take[#, Ordering[#, -1]] &@(Reverse /@ #) &@ list
(*
-> {{5, 10}}
*)
используя тот факт, что Ordering[ ] списки заказов по их первому элементу
редактировать
или гораздо лучше (я думаю):
Take[#, Ordering[Last /@ #, -1]] &@ list
редактировать
также:
#[[Ordering[#, -1, Last@#2 > Last@#1 &]]] &@list
редактировать
возможно быстрее:
#[[First@Position[#, Max@#] &@(Last /@ #)]] &@list
вот мой подход, используя Pick
maxBy[list_, n_] := With[{s = list[[All, n]]}, Pick[list, s, Max[s]]]
maxBy[{{4, 3}, {5, 10}, {-2, 1}, {3, 7}}, 2]
(* output:
{{5, 10}}
*)
эта версия работает на любом количестве элементов в подсписке, предусмотренного n меньше или равно длине самого короткого подсписка.
тайминги для этой версии на моей машине
list2 = RandomInteger[{-10^7, 10^7}, {10^6, 2}];
list3 = RandomInteger[{-10^7, 10^7}, {10^6, 3}];
list9 = RandomInteger[{-10^7, 10^7}, {10^6, 9}];
maxBy[list2, 2]; // Timing
maxBy[list3, 2]; // Timing
maxBy[list9, 2]; // Timing
(* output:
{0.030341, Null}
{0.030912, Null}
{0.033313, Null}
*)
по сравнению с кодом Дэвида
maxBy[list2, 2]; // Timing
maxBy[list3, 2]; // Timing
maxBy[list9, 2]; // Timing
(* ouput:
{0.186175, Null}
{0.184989, Null}
{0.262018, Null}
*)
Йоды код
maxBy[list2, 2]; // Timing
maxBy[list3, 2]; // Timing
maxBy[list9, 2]; // Timing
(* ouput:
{0.944016, Null}
{0.83094, Null}
{0.874126, Null}
*)
и Велисария код
Reverse /@ Take[#, Ordering[#, -1]] &@(Reverse /@ #) &@list2; // Timing
Take[#, Ordering[Last /@ #, -1]] &@list2; // Timing
#[[Ordering[#, -1, Last@#2 > Last@#1 &]]] &@list2; // Timing
#[[First@Position[#, Max@#] &@(Last /@ #)]] &@list2; // Timing
(* output:
{0.211016, Null}
{0.099253, Null}
{2.03415, Null}
{0.266934, Null}
*)
Как насчет этой функции (определенной здесь только для 2D-списков):
maxBy = Module[{pattern = Reverse@Insert[{Max@#1[[All, #2]]}, _, #2]},
Cases[#1, pattern]] &
пример:
list = {{4, 3}, {5, 10}, {20, 1}, {3, 7}};
maxBy[list, 1]
Out[1]= {{20, 1}}
maxBy[list, 2]
Out[2]= {{5, 10}}
вот подход, который опирается на Transpose:
maxBy = #1[[Position[t = Transpose[#1][[#2]], Max[t]][[All, 1]]]] &;
например: список = {{4, 3}, {5, 10}, {20, 1}, {3, 7}};
maxBy[list, 1]
(* {{20, 1}} *)
maxBy[list, 2]
(* {{5, 10}} *)
он может обрабатывать более двух элементов в подсписке, при условии, что подсписки имеют одинаковую длину.
r:=RandomInteger[{-10^5,10^5}];
list3=Table[{r,r,r},{j,10^2}]; (* 3 numbers in each sublist *)
list9=Table[{r,r,r,r,r,r,r,r,r},{j,10^2}]; (* 9 numbers *)
maxBy[list3, 2] (* Find max in position 2 of list3 *)
(* {{-93332, 99582, 4324}} *)
maxBy[list9, 5] (* Find max in position 5 of list9 *)
(* {{7680, 85508, 51915, -58282, 94679, 50968, -12664, 75246, -82903}} *)
конечно, результаты будут варьироваться в зависимости от случайных чисел, который вы породили.
редактировать
вот некоторые данные синхронизации для больших списков. SortBy is явно медленнее. но, похоже, на это не влияет количество элементов в каждом подсписке. Во-первых, мой maxBy код, за которым следует SortBy:
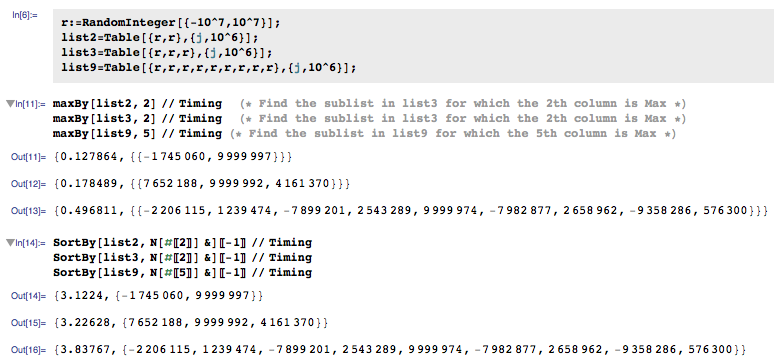
используя тот же list2, вот некоторые данные о времени для кода Йоды. Хотя его режим также называется maxBy, это его, который произвел результат, который следует:
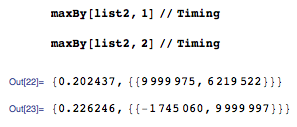
опять же, с тем же list2, некоторые данные для кода Велисария:

второй предложение является самым быстрым из всех проверенных.
не самый эффективный, но проще?
max = Max@list[[All, -1]];
Cases[list, {_, max}]
или
max = Max@list3[[All, -1]];
Cases[list3, {_,_, max}]
использование
list = {{40, 3}, {5, 10}, {-2, 1}, {3, 10}}
max = Max@list[[All, -1]];
Cases[list, {_, max}]
выход:
{{5, 10}, {3, 10}}
после прочтения некоторых документов и проведения нескольких экспериментов мне удалось получить более четкое представление об этой проблеме.
на самом деле мне было интересно, почему Max[] казалось намеренно избегать предоставления директив, которые заставляют его возвращать не только сам элемент max, но и его положение. В конце концов, предоставление позиции не меняет сложности алгоритма O(n). Например, представьте себе:
In[1]:= Max[{991, 993, 992}, ReturnPosition -> True]
Out[1]= {2}
если это можно сделать, вы можете просто использовать код ниже, чтобы решите мою проблему:
list[[Max[list[[All, -1]], ReturnPosition -> True]]]
но теперь я понимаю, что функции системы Max[] is не предназначен для поиска элемента max в списки. Вы можете сказать, что команда Wolfram явно сделала Max[] больше похоже на традиционный max функция в математике-она делает простые символические упрощения, она автоматически выравнивает все списки, она может быть в plotable функции, и самое главное, это Orderless:
In[2]:= Attributes[Max]
Out[2]= {Flat, NumericFunction, OneIdentity, Orderless, Protected}
что делает позиции бессмысленными. Одним словом, он рассматривает все списки внутри как математические множества.
так философски это не тривиально для Mathematica, чтобы вычислить это. Все, что мне нужно сделать, это "DIY" функцию со сложностью O(n) и может выполнять эту работу. Я думаю, что TomD движется в правильном направлении, хотя я предпочитаю:
maxLast[l_] := Cases[l, {___, Max[Last/@l]}]
и Хэйке (黑客?) принято Pick которые могут иметь лучшие методы, специально предназначенные для выбора элементов, но не должны быть виртуальными разница в сложности алгоритма. И я могу переписать его так: (меньше имен и голов, быстрее скорость)
maxLast[l_] := Pick[l, #, Max[#]] &[Last /@ l]
они оба хорошие ответы.
