Какова полезность Boost Polygon?

это вопрос о Boost Polygon (не о геометрии Boost)

недавно я пытался играть с некоторыми геометрическими многоугольными конструкциями. С Ускорение Геометрия (a разные библиотека, которая также имеет дело с полигонами) не работает косвенно в Boost 1.58 I, хотя я бы попытался Увеличить Полигона.

после попытки понять библиотеку и не получить ожидаемых результатов я обнаружил, что библиотека работает только для целочисленных координат. сначала я думал, что это ограничение для ввода, но на самом деле все внутренние операции и выходы являются целыми числами, это делает все выходные довольно причудливыми, например, пересечения для полигонов слегка деформированы (потому что координаты вершин должны быть целыми).

цитата с главной страницы (акцент мой):

тип данных координат - это шаблон параметр всех типов данных и алгоритмы, предоставляемые библиотекой, и ожидается, что будет интегральным. типы данных координат с плавающей запятой не поддерживаются по алгоритмы, реализованные в библиотеке, обусловлены тем, что (sic) достижение устойчивости с плавающей запятой подразумевает другой набор алгоритмы и, как правило, специфические для платформы предположения о плавании точечные представления.

сначала я думал, что это было проблема между точным и неточным представлением, поэтому я попытался заставить его работать с рациональными (Boost Rational) типами (я вычислил рациональный класс оболочки, чтобы он компилировался), но на самом деле целочисленные координаты являются строгим требованием (в коде есть части, которые фактически добавляют и вычитают один для создания промежуточных результатов).

возвращаясь к целым числам, я должен был сделать координаты очень большими (в целочисленных терминах), чтобы эта проблема дискретности исчезла. Другими словами Я надо все нормализовать туда-сюда. Ну, в конце концов, это не очень полезно или удобно, как я изначально думал.

я пропустил что-то важное об использовании этой библиотеки?

предназначена ли эта библиотека для" пиксельных " проблем? Что такое утилита, если координаты ограничены целыми числами?

идея масштабировать координаты до очень больших чисел, а затем перенормировать результаты позже для геометрических приложений?

Я понимаю, что вычислительная геометрия с плавающими точками очень болезненна,но почему эта библиотека даже не пытается быть совместимым с точным рационалы?

есть ли реальные примеры использования? (руководство довольно плохо дает примеры)кто-нибудь действительно использует эту библиотеку?

бонус-вопрос: это заброшенный библиотека?

это пример того, как библиотека ведет с целочисленными координатами:

вот пример того, что происходит с интегральными полигонами, если я использую небольшие числа для представления координат, результаты даже не геометрически согласованы. (Два многоугольника -polygon(-2,0)(2,-2)(6,4)(0,2) и polygon(-5,0)(-1,-2)(3,4)(-3,2))

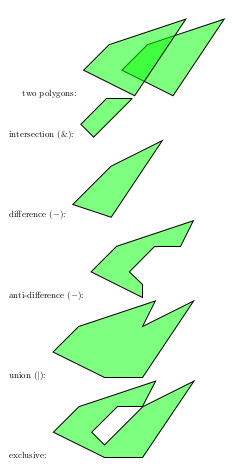
(обратите внимание, как перекос все выходит.)

но когда я масштабировать полигоны имеют большие целочисленные координаты, результаты становятся более точными (два полигона polygon(-200,0)(200,-200)(600,400)(0,200) и polygon(-500,0)(-100,-200)(300,400)(-300,200), масштабированные версии двух выше.):

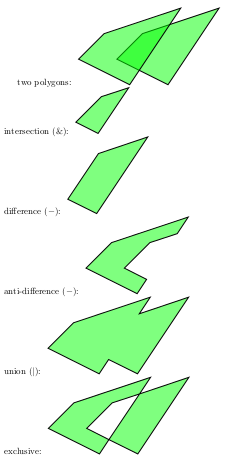
EDIT: я узнал немного больше о вычислительной геометрии, по-видимому, устойчивость вычислительной геометрии-очень сложная проблема. Одна из стратегий заключается в использовании целочисленной арифметики. Похоже на ускорение.Polygon использует этот подход. Проблемы в непрерывном пространстве должны масштабироваться соответствующим образом.