Какова вероятность столкновения md5, если я пройду в 2^32 наборах строк?

этот вопрос похож на так называемый "парадокс дней рождения".

в теории вероятностей проблема рождения или парадокс дней рождения касается вероятности того, что в наборе n случайно выбранные люди, некоторые из них будут иметь один и тот же день рождения. По принципу Дирихле, вероятность достигает 100%, когда количество людей достигает 367 (так как есть 366 возможных дней рождения, в том числе 29 февраля). Однако 99% вероятности достигается только с 57 людьми, и 50% вероятности с 23 людьми. Эти выводы основаны на предположении, что каждый день года (кроме 29 февраля) одинаково вероятен для дня рождения.

математика, стоящая за этой проблемой, привела к известной криптографической атаке под названием день рождения атака, который использует эту вероятностную модель для уменьшения сложности взлома хэша функция.

согласно статье Википедии, вероятность столкновения при выборе n = 2³² случайные числа из космоса с d = 2¹²⁸ цифры примерно:

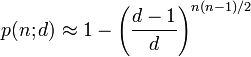
Если вы проработайте этот расчет шанс составляет около 2,7×10^-20. Это очень небольшая вероятность, но обратите внимание, что она на 9 порядков выше вашей предлагаемый расчет.