Какой алгоритм используют калькуляторы для поиска значений синуса?
Если кто-то дает мне угол, скажем, 38 градусов, как я узнаю значение синусоидальной функции для его значения, не используя фактически создание правильного треугольника с 38 градусов и измерения сторон? Я знаю, что могу использовать некоторые тригонометрические тождества, чтобы приблизиться к значениям, но это было бы трудоемко.
Я уверен, что алгоритмы, используемые в калькуляторах и компьютерах, не будут прибегать к этому. Например, если мне нужно найти pi, я буду использовать такой алгоритм :
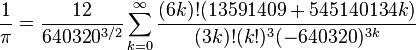
вместо того, чтобы получить компас и линейку и рисовать круги.
однако я не могу найти такой алгоритм для синусоидальной функции.
может кто-то пожалуйста, помогите мне с этим?
3 ответов
один из наиболее распространенных алгоритмов для этого-взять первые несколько членов ряда Тейлора для синуса.
sin x = x - x3/3! + x5/5! - x7/7! + ...,
чем больше терминов вы берете, тем лучшее приближение вы получаете. X находится в радианах здесь, но вы можете получить радианы от градусов довольно легко. И тогда, как вы видите, для вычисления синуса можно использовать только основные операции:+, -,*,/.
в машинах с чипами сопроцессора с плавающей запятой используется алгоритм CORDIC (с несколькими другими модулями), так как он также может быть реализован в аппаратном обеспечении.
улучшение ответа Джона:
создайте таблицу sin (x) для x в разных радианах от 0 до pi/2.
вы можете использовать интерполяцию следующим образом: sin (x+dx) = sin(x) + dx*cos(x)
cos(x) = sin (pi/2-x).
аналогично, cos(x+dx) = cos(x) - dx*sin (x).
Я не знаю, что на самом деле используется любыми калькуляторами, но таблица поиска с линейной (или более высокого порядка, если хотите) интерполяцией должна быть простой и достаточно точной для 3 мест точности или более плотной таблицы. Вам нужно будет только столик на одну четверть цикла и может использовать его для всех синусов и косинусов с помощью соответствующих преобразований. Если у вас достаточно мощности и точности, вы можете попробовать повторить серию Тейлора или что-то еще, но ошибки округления будут накопить на вы.
