Какой алгоритм определяет близость точки к кривой Безье?

вы можете сделать это analitically, но нужно немного математики.

кривая Безье может быть выражена в терминах Основы Бернштейн. Здесь я буду использовать Mathematica, что обеспечивает хорошую поддержку математике.

так что если у вас есть вопросы:

pts = {{0, -1}, {1, 1}, {2, -1}, {3, 1}};  

эквалайзер. для кривой Безье:

f[t_] := Sum[pts[[i + 1]] BernsteinBasis[3, i, t], {i, 0, 3}];

имейте в виду, что я использую базис Бернштейна для удобства, но любой параметрический представление кривой Безье было бы достаточно.

что дает:

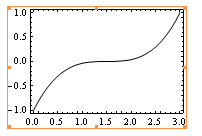
теперь, чтобы найти минимальное расстояние до точки (например, {3, -1}), вы должны минимизировать функцию:

d[t_] := Norm[{3, -1} - f[t]];  

для этого вам нужен алгоритм минимизации. У меня есть один под рукой, так что:

NMinimize[{d[t], 0 <= t <= 1}, t]  

выдает:

 {1.3475, {t -> 0.771653}}  

и это все.

HTH!

редактировать относительно вашего редактирования "B-сплайн с состоящими из (n-1)/3 кубических кривых Безье."

если вы построили кусочное представление B-сплайна, вы должны перебирать все сегменты, чтобы найти минимумы. Если вы объединили части по непрерывному параметру, то этот же подход будет делать.

редактировать

решение вашей кривой. Я игнорирую первый пункт, потому что я действительно не понял, что это такое.

я решил его с помощью стандартных Bsplines вместо функций mathematica, ради ясности.

Clear["Global`*"];
(*first define the points *)
pts = {{
        29.124, 284.61}, {
        25.066, 258.56}, {
        20.926, 212.47}, {
        34, 176}, {
        38.706, 162.87}, {
        46.556, 149.82}, {
        54.393, 138.78}};

(*define a bspline template function *)

b[t_, p0_, p1_, p2_, p3_] :=
                  (1-t)^3 p0 + 3 (1-t)^2 t p1 + 3 (1-t) t^2 p2 + t^3 p3;

(* define two bsplines *)
b1[t_] := b[t, pts[[1]], pts[[2]], pts[[3]], pts[[4]]];
b2[t_] := b[t, pts[[4]], pts[[5]], pts[[6]], pts[[7]]];

(* Lets see the curve *)

Show[Graphics[{Red, Point[pts], Green, Line[pts]}, Axes -> True], 
 ParametricPlot[BSplineFunction[pts][t], {t, 0, 1}]]

. (Вращается ! для экономии места на экране )

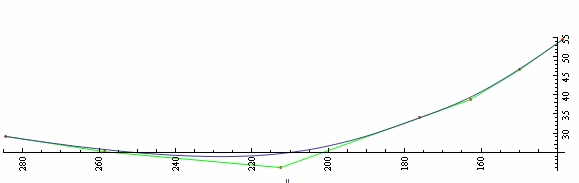
(*Now define the distance from any point u to a point in our Bezier*)
d[u_, t_] := If[(0 <= t <= 1), Norm[u - b1[t]], Norm[u - b2[t - 1]]];

(*Define a function that find the minimum distance from any point u \
to our curve*)
h[u_] := NMinimize[{d[u, t], 0.0001 <= t <= 1.9999}, t];

(*Lets test it ! *)
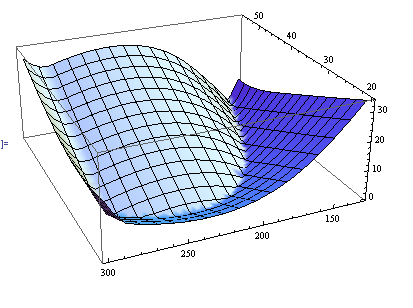
Plot3D[h[{x, y}][[1]], {x, 20, 55}, {y, 130, 300}]

этот график является (минимальным) расстоянием от любой точки в пространстве до нашей кривой (конечно, значение по кривой равно нулю):