Какой самый быстрый способ подсчета элементов в массиве?

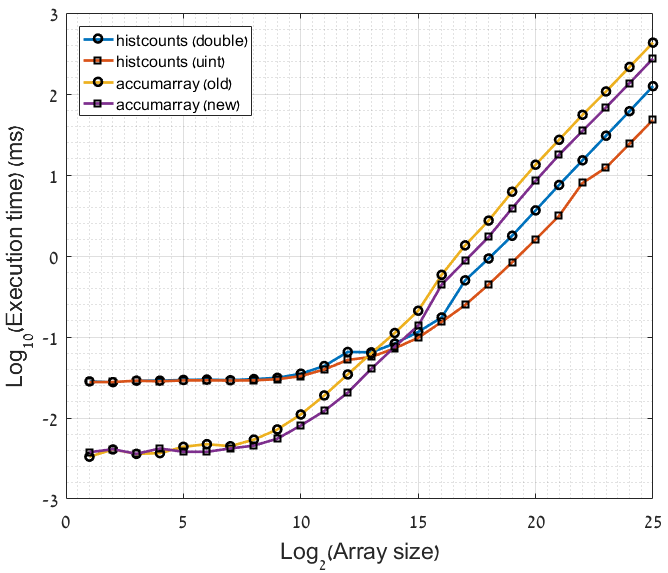
tl; dr: самый быстрый метод зависит от размера массива. Для массива меньше 2¹⁴ метод 3 ниже (accumarray) быстрее. Для массивов больше, чем этот метод 2 ниже (histcounts) лучше.

UPDATE: я тестировал это также с неявное вещания, который был введен в 2016b, и результаты почти равны bsxfun подход, без существенной разницы (относительно других методов) в этом метод.

---

давайте посмотрим, каковы доступные методы для выполнения этой задачи. Для следующих примеров мы предположим X и n элементы, от 1 до n, и наш массив интереса M, который представляет собой массив столбцов, который может отличаться по размеру. Наш вектор результатов будет spp¹, таких, что spp(k) число ks в M. Хотя я пишу здесь о X, в коде нет явной реализации этого ниже я просто определяю n = 500 и X неявно 1:500.

наивный for цикл

Самый простой и простой способ справиться с этой задачей-это for цикл, который повторяет элементы в X и подсчитайте количество элементов в M это равно:

function spp = loop(M,n)
spp = zeros(n,1);
for k = 1:size(spp,1);
    spp(k) = sum(M==k); 
end
end

это, конечно, не так умно, особенно если только небольшая группа элементов из X заполнение M, поэтому нам лучше сначала поискать те, что уже в M:

function spp = uloop(M,n)
u = unique(M); % finds which elements to count
spp = zeros(n,1);
for k = u(u>0).';
    spp(k) = sum(M==k); 
end
end

---

обычно в MATLAB рекомендуется максимально использовать встроенные функции, так как в большинстве случаев они намного быстрее. Я подумал о 5 вариантах сделать это:

1. Функция tabulate

Функция tabulate возвращает очень удобную таблицу частот, которая на первый взгляд кажется идеальным решением для этого задача:

function tab = tabi(M)
tab = tabulate(M);
if tab(1)==0
    tab(1,:) = [];
end
end

единственное исправление, которое нужно сделать, это удалить первую строку таблицы, если она подсчитывает 0 элемент (возможно, в M).

2. Функция histcounts

Еще один вариант, который можно настроить довольно легко для нашей потребности в нем histcounts:

function spp = histci(M,n)
spp = histcounts(M,1:n+1);
end

здесь, чтобы подсчитать все различные элементы от 1 до n отдельно, мы определяем края 1:n+1, так что каждый элемент в X имеет свой собственный ящик. Мы могли бы написать также histcounts(M(M>0),'BinMethod','integers'), но я уже тестировал его, и это занимает больше времени (хотя это делает функцию независимой от n).

3. Функция accumarray

Следующий вариант, который я приведу здесь, - это использование функции accumarray:

function spp = accumi(M)
spp = accumarray(M(M>0),1);
end

здесь мы даем функцию M(M>0) в качестве ввода, чтобы пропустить нули и использовать 1 как vals вход для подсчета всех уникальных элементы.

4. Функция bsxfun

Мы даже можем использовать двоичную операцию @eq (т. е. ==) искать все элементы из каждого типа:

function spp = bsxi(M,n)
spp = bsxfun(@eq,M,1:n);
spp = sum(spp,1);
end

если мы сохраним первый вход M и второй 1:n в разных измерениях, поэтому один столбец вектора в другой вектор-строку, то функция сравнивает каждый элемент M С каждым элементом в 1:n, и создать length(M) - by -n логические матрица, чем мы можем суммировать, чтобы получить желаемый результат.

5. Функция ndgrid

Другой вариант, похожий на bsxfun, чтобы явно создать две матрицы всех возможностей, используя