Кэш-дружественное копирование массива с перестройкой по известному индексу, сбор, разброс
Предположим у нас есть массив данных и другой массив с индексами.
data = [1, 2, 3, 4, 5, 7]
index = [5, 1, 4, 0, 2, 3]
мы хотим создать новый массив из элементов data на должность от index. Результат должен быть
[4, 2, 5, 7, 3, 1]
наивный алгоритм работает для O (N), но он выполняет случайный доступ к памяти.
можете ли вы предложить дружественный алгоритм кэша процессора с той же сложностью.
PS В моем случае все элементы в массиве данных являются целыми числами.
PPS Матрицы может содержать миллионы элементов.
PPPS я в порядке с SSE / AVX или любыми другими оптимизациями x64
7 ответов
объединить индекс и данные в один массив. Затем используйте некоторый удобный для кэша алгоритм сортировки для сортировки этих пар (по индексу). Тогда избавьтесь от индексов. (Вы можете объединить слияние / удаление индексов с первым / последним проходом алгоритма сортировки, чтобы немного оптимизировать это).
для кэш-дружественных O (N) сортировки используйте сортировку radix с достаточно малым radix (не более половины количества строк кэша в кэше CPU).
вот реализация c radix-sort-like алгоритм:
void reorder2(const unsigned size)
{
const unsigned min_bucket = size / kRadix;
const unsigned large_buckets = size % kRadix;
g_counters[0] = 0;
for (unsigned i = 1; i <= large_buckets; ++i)
g_counters[i] = g_counters[i - 1] + min_bucket + 1;
for (unsigned i = large_buckets + 1; i < kRadix; ++i)
g_counters[i] = g_counters[i - 1] + min_bucket;
for (unsigned i = 0; i < size; ++i)
{
const unsigned dst = g_counters[g_index[i] % kRadix]++;
g_sort[dst].index = g_index[i] / kRadix;
g_sort[dst].value = g_input[i];
__builtin_prefetch(&g_sort[dst + 1].value, 1);
}
g_counters[0] = 0;
for (unsigned i = 1; i < (size + kRadix - 1) / kRadix; ++i)
g_counters[i] = g_counters[i - 1] + kRadix;
for (unsigned i = 0; i < size; ++i)
{
const unsigned dst = g_counters[g_sort[i].index]++;
g_output[dst] = g_sort[i].value;
__builtin_prefetch(&g_output[dst + 1], 1);
}
}
он отличается от сортировки radix в двух аспектах: (1) он не делает подсчет проходов, потому что все счетчики известны заранее; (2) он избегает использования значений power-of-2 для radix.
этот код C++ использовался для бенчмаркинга (если вы хотите запустить его на 32-битной системе, слегка уменьшить kMaxSize константы).
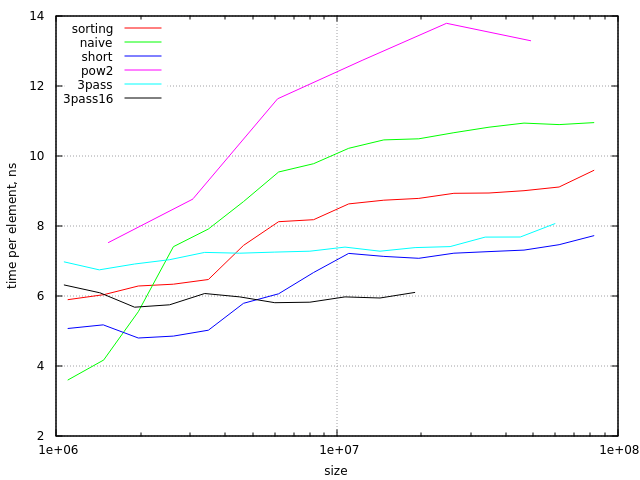
вот результаты тестов (на процессоре Haswell с 6Mb cache):
легко видеть, что небольшие массивы (ниже ~2 000 000 элементов) кэширование, даже для наивного алгоритма. Также вы можете заметить, что подход сортировки начинает быть кеш-недружественным в последней точке диаграммы (с size/radix около 0.75 строк кэша в кэше L3). Между этими пределами сортировка более эффективна, чем наивный алгоритм.
теоретически (если мы сравним только пропускную способность памяти, необходимую для этих алгоритмы с 64-байтовыми линиями кэша и 4-байтовыми значениями) алгоритм сортировки должен быть в 3 раза быстрее. На практике мы имеем гораздо меньшую разницу, около 20%. Это может быть улучшено, если мы используем меньшие 16-битные значения для data массив (в этом случае алгоритм сортировки примерно в 1,5 раза быстрее).
еще одна проблема с подходом сортировки-его наихудшее поведение, когда size/radix находится слишком близко к какой-питания-в-2. Это может быть либо проигнорировано (потому что не так много "плохих" размеров), либо исправлено делает этот алгоритм немного сложнее.
если мы увеличим количество проходов до 3, Все 3 прохода используют в основном кэш L1, но пропускная способность памяти увеличивается на 60%. Я использовал этот код для получения экспериментальных результатов:TL; DR. После определения (экспериментально) лучшего значения radix я получил несколько лучшие результаты для размеров больше 4 000 000 (где алгоритм 2-pass использует кэш L3 для одного прохода), но несколько худшие результаты для меньших массивов (где алгоритм 2-pass использует Кэша L2 для обоих проходов). Как и следовало ожидать, производительность лучше для 16-битных данных.
вывод: разница в производительности намного меньше, чем разница в сложности алгоритмов, поэтому наивный подход почти всегда лучше; если производительность очень важна и используются только значения 2 или 4 байта, предпочтительнее подход сортировки.
data = [1, 2, 3, 4, 5, 7]
index = [5, 1, 4, 0, 2, 3]мы хотим создать новый массив из элементов данных на позициях от индекс. Результат должен быть
result -> [4, 2, 5, 7, 3, 1]
один поток, один проход
Я думаю, для нескольких миллионов элементов и на один поток на наивный подход может быть лучшим здесь.
и data и index доступны (читай) последовательно, что уже оптимально для кэша CPU. Это оставляет случайную запись, но запись в память не так удобна для кэша, как чтение из нее.
для этого понадобится только один последовательный pass через данные и индекс. И, скорее всего, некоторые (иногда многие) из них уже будут кэш-friendly тоже.
использование нескольких блоков для result - несколько потоков
мы могли бы выделить или использовать кэш-дружественные блоки размера для результата (блоки, являющиеся регионами в result array), и петля через index и data несколько раз (пока они остаются в кэше).
в каждом цикле мы затем пишем только элементы в result это вписывается в текущий результат-блок. Это было бы "дружественным к кэшу" для записи тоже, но требует нескольких циклов (количество циклов может даже получить довольно высокое-т. е. size of data / size of result-block).
вышеуказанное может быть вариантом когда используя несколько потоков: data и index, будучи только для чтения, будет совместно использоваться всеми ядрами на некотором уровне в кэше (в зависимости от архитектуры кэша). The result блоки в каждом потоке будут полностью независимыми (одному ядру никогда не придется ждать результата другого ядра или записи в том же регионе). Например: 10 миллионов элементов - каждый поток может работать над независимым результирующим блоком, скажем, 500.000 элементов (число должно быть 2).
объединение значений в пару и сортировка их сначала: это уже займет гораздо больше времени, чем наивный вариант (и также не будет дружественным к кэшу).
кроме того, если есть только несколько миллионов элементов (целых чисел), это не будет иметь большого значения. Если мы говорим о миллиардах или данных, которые не вписываются в память, могут быть предпочтительны другие стратегии (например, сопоставление памяти с результирующим набором, если не вписывается в память).
Если ваша проблема связана с гораздо большим количеством данных, чем вы показываете здесь, самым быстрым способом - и, вероятно, самым удобным для кэша - было бы выполнить большую и широкую операцию сортировки слиянием.
таким образом, вы разделите входные данные на разумные куски и будете иметь отдельный поток для каждого куска. Результатом этой операции будут два массива, подобные входным (один индекс данных и один целевой индекс), однако индексы будут отсортированы. Тогда у вас будет последняя нить сделать операция слияния данных в конечный выходной массив.
пока сегменты выбраны хорошо, это должен быть довольно удобный алгоритм для кэша. Мудро я имею в виду, что данные, используемые различными потоками, отображаются на разные строки кэша (выбранного вами процессора), чтобы избежать кэширования.
Если у вас много данных, и это действительно горлышко бутылки, вам нужно будет использовать алгоритм на основе блоков, где вы читаете и пишете из тех же блоков, насколько это возможно. Это займет до 2 проходов по данным, чтобы гарантировать, что новый массив полностью заполнен, и размер блока должен быть установлен соответствующим образом. Псевдокод ниже.
def populate(index,data,newArray,cache)
blockSize = 1000
for i = 0; i < size(index); i++
//We cached this value earlier
if i in cache
newArray[i] = cache[i]
remove(cache,i)
else
newIndex = index[i]
newValue = data[i]
//Check if this index is in our block
if i%blockSize != newIndex%blockSize
//This index is not in our current block, cache it
cache[newIndex] = newValue
else
//This value is in our current block
newArray[newIndex] = newValue
cache = {}
newArray = []
populate(index,data,newArray,cache)
populate(index,data,newArray,cache)
анализ
наивное решение обращается к индексу и массива данных в порядке, но новый массив осуществляется в произвольном порядке. Поскольку новый массив доступен случайным образом, вы в конечном итоге получаете O (N^2), где N-количество блоков в массиве.
решение на основе блока не переходит из блока в блок. Он считывает индекс, данные и новый массив последовательно для чтения и записи в одни и те же блоки. Если индекс будет находиться в другом блоке, он кэшируется и либо извлекается, когда появляется блок, к которому он принадлежит, либо если блок уже передан, он будет извлечен в второй пас. Второй проход совсем не повредит. Это O (N).
единственное предостережение заключается в работе с кэшем. Есть много возможностей для творчества здесь, но в целом, если много читает и пишет на разных блоках кэш будет расти и это не оптимально. Это зависит от состава ваших данных, как часто это происходит и реализация кэша.
давайте представим, что вся информация внутри кэша существует в одном блоке и это вписывается в память. И скажем, что кэш имеет y элементов. Наивный подход имел бы случайный доступ по крайней мере y раз. Блок на основе подхода получит те, во втором проходе.
Я заметил, что ваш индекс полностью покрывает домена, но в случайном порядке.
Если бы вы сортировали индекс, но также применяли те же операции к массиву индексов к массиву данных, массив данных стал бы результатом, который вы ищете.
существует множество алгоритмов сортировки для выбора, все они удовлетворяют вашим дружественным критериям кэша. Но их сложность различна. Я бы подумал о quicksort или mergesort.
Если вас интересует этот ответ Я могу разработать псевдокод.
Я обеспокоен тем, что это может быть не выигрышный шаблон.
У нас был фрагмент кода, который работал хорошо, и мы оптимизировали его, удалив копию.
в результате он работал плохо (из-за проблем с кэшем). Я не вижу, как вы можете создать алгоритм с одним проходом, который решает проблему. Использование OpenMP может позволить киоскам, которые это приведет к разделению между несколькими потоками.
Я предполагаю, что переупорядочение происходит только один раз таким же образом. Если это происходит несколько раз, то создание лучшей стратегии заранее (и соответствующий алгоритм сортировки) улучшит производительность
Я написал следующую программу, чтобы фактически проверить, помогает ли простое разделение цели на N блоков, и мой вывод был:
a) даже в худших случаях было невозможно, чтобы производительность одного потока (с использованием сегментированных записей) не превышала наивную стратегия, и обычно хуже, по крайней мере, в 2 раза
b) однако производительность приближается к единству для некоторых подразделений (вероятно, зависит от процессора) и размеров массива, что указывает на то, что это действительно улучшит многоядерную производительность
следствием этого является: Да, это более "кэш-дружественный", чем не разделение, но для одного потока (и только одного переупорядочения) это не поможет вам немного.
#include <stdlib.h>
#include <stdio.h>
#include <sys/time.h>
void main(char **ARGS,int ARGC) {
int N=1<<26;
double* source = malloc(N*sizeof(double));
double* target = malloc(N*sizeof(double));
int* idx = malloc(N*sizeof(double));
int i;
for(i=0;i<N;i++) {
source[i]=i;
target[i]=0;
idx[i] = rand() % N ;
};
struct timeval now,then;
gettimeofday(&now,NULL);
for(i=0;i<N;i++) {
target[idx[i]]=source[i];
};
gettimeofday(&then,NULL);
printf("%f\n",(0.0+then.tv_sec*1e6+then.tv_usec-now.tv_sec*1e6-now.tv_usec)/N);
gettimeofday(&now,NULL);
int j;
int targetblocks;
int M = 24;
int targetblocksize = 1<<M;
targetblocks = (N/targetblocksize);
for(i=0;i<N;i++) {
for(j=0;j<targetblocks;j++) {
int k = idx[i];
if ((k>>M) == j) {
target[k]=source[i];
};
};
};
gettimeofday(&then,NULL);
printf("%d,%f\n",targetblocks,(0.0+then.tv_sec*1e6+then.tv_usec-now.tv_sec*1e6-now.tv_usec)/N);
};