Код Python: геометрическое броуновское движение-что случилось?

Я довольно новичок в Python, но для работы в университете мне нужно применить некоторые модели, используя предпочтительно Python. Я провел пару дней с кодом, который я прикрепил, но я не могу помочь, что не так, это не создает случайный процесс, который выглядит как стандартные броуновские движения с дрейфом. Мои параметры, такие как mu и sigma (ожидаемый доход или дрейф и волатильность), имеют тенденцию изменять только наклон шумового процесса. Это моя проблема, все выглядит как шум. Надеюсь моя проблема достаточно конкретно, вот мой coode:

import math
from matplotlib.pyplot import *
from numpy import *
from numpy.random import standard_normal

'''
geometric brownian motion with drift!

Spezifikationen:

    mu=drift factor [Annahme von Risikoneutralitaet]
    sigma: volatility in %
    T: time span
    dt: lenght of steps
    S0: Stock Price in t=0
    W: Brownian Motion with Drift N[0,1] 
'''

T=1
mu=0.025
sigma=0.1
S0=20
dt=0.01

Steps=round(T/dt)

t=(arange(0, Steps))
x=arange(0, Steps)
W=(standard_normal(size=Steps)+mu*t)### standard brownian motion###
X=(mu-0.5*sigma**2)*dt+(sigma*sqrt(dt)*W) ###geometric brownian motion####
y=S0*math.e**(X)

plot(t,y)

show()
8
finance python random-walk stochastic

2 ответов

по данным Википедия,

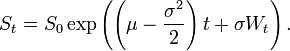
enter image description here

получается, что

X=(mu-0.5*sigma**2)*t+(sigma*W) ###geometric brownian motion####

, а не

X=(mu-0.5*sigma**2)*dt+(sigma*sqrt(dt)*W)

С T представляет временной горизонт, я думаю t должно быть

t = np.linspace(0, T, N)

теперь, согласно этим примерам Matlab (здесь и здесь), он появляется

W = np.random.standard_normal(size = N) 
W = np.cumsum(W)*np.sqrt(dt) ### standard brownian motion ###

нет,

W=(standard_normal(size=Steps)+mu*t)

пожалуйста, проверьте математику, однако я могу ошибаться.

Итак, собрав все вместе:

import matplotlib.pyplot as plt
import numpy as np

T = 2
mu = 0.1
sigma = 0.01
S0 = 20
dt = 0.01
N = round(T/dt)
t = np.linspace(0, T, N)
W = np.random.standard_normal(size = N) 
W = np.cumsum(W)*np.sqrt(dt) ### standard brownian motion ###
X = (mu-0.5*sigma**2)*t + sigma*W 
S = S0*np.exp(X) ### geometric brownian motion ###
plt.plot(t, S)
plt.show()

доходность

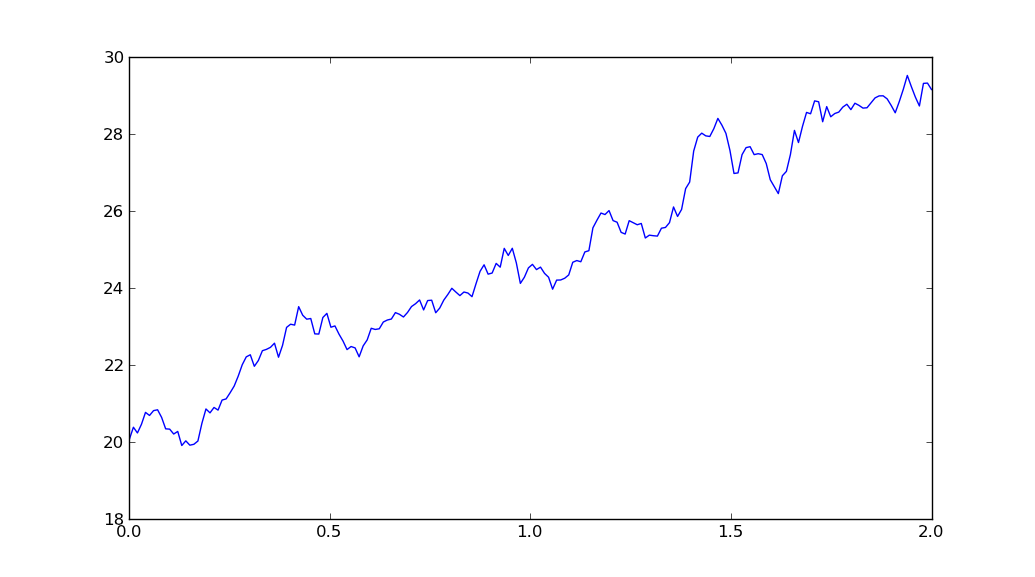
enter image description here

18

дополнительная реализация, использующая параметризацию гауссова закона, хотя нормальный fonction (вместо standard_normal), немного короче.

import numpy as np

T = 2
mu = 0.1
sigma = 0.01
S0 = 20
dt = 0.01
N = round(T/dt)
# reversely you can specify N and then compute dt, which is more common in financial litterature

X = np.random.normal(mu * dt, sigma* np.sqrt(dt), N)
X = np.cumsum(X)
S = S0 * np.exp(X)
0