Когда выгодно конвертировать из float в double через decimal

как ни странно, преобразование через decimal (с Convert.ToDecimal(float)) может быть полезным в некоторых обстоятельствах.

это улучшит точность, если известно, что исходные номера были предоставлены пользователями в десятичном представлении и пользователи набрали не более 7 значащих цифр.

чтобы доказать это, я написал небольшую программу (см. ниже). Вот объяснение:

как вы помните из OP, это последовательность шагов:

1. приложение B имеет двойники, поступающие из двух источников: (a) результаты расчетов; (b) преобразованные из введенных пользователем десятичных чисел.
2. приложение B записывает свои двойники как поплавки в файл-эффективно выполнение двоичного округления из 52 двоичных цифр ( IEEE 754 одиночный) до 23 двоичных цифр (IEEE 754 двойной).

3. наше приложение считывает этот float и преобразует его в double одним из двух способов:

   (a) прямое назначение двойного эффективного заполнения 23 - разрядного числа 52-разрядным числом с двоичными нулями (29 нулевых битов);

   (b) через преобразование в десятичное с (double)Convert.ToDecimal(float).

Как правильно заметил Бен Фойгта Convert.ToDecimal(float) (см. MSDN в разделе Примечания) округляет результат до 7 значащих десятичных цифр. В Википедии IEEE 754 article о сингле мы можем прочитать, что precision is 24 bits - equivalent to log10(pow(2,24)) ≈ 7.225 decimal digits. Итак, когда мы делаем преобразование в decimal мы теряем 0.225 десятичной цифры.

Итак, в общем случае, когда нет дополнительной информации о двойниках, преобразование в десятичное в большинстве случаев заставит нас потерять некоторую точность.

но (!) если есть дополнительные знания о том, что первоначально (до записи в файл в виде поплавков) двойники были десятичными числами не более 7 цифр, ошибки округления, введенные в десятичном округлении (Шаг 3 b) выше)компенсирует ошибки округления, введенные с двоичным округлением (в шаге 2. выше.)

в программе, чтобы доказать утверждение для общего случая я произвольно генерирую двойные, затем бросаю его в float, затем преобразую его обратно в double (a) напрямую, (b) через decimal, затем я измеряю расстояние между исходным double и double (a) и double (b). Если double (a) ближе к оригиналу, чем double (b), I increment Pro-direct conversion counter, в противоположном случае я увеличиваю Pro-viaDecimal счетчик. Я делаю это в цикле 1 млн. циклы, затем я печатаю отношение Pro-direct к pro-viaDecimal счетчикам. Соотношение получается около 3.7, т. е. примерно в 4 случаях из 5 преобразование через десятичный испортят количество.

доказать случай, когда номера вводятся пользователями я использовал ту же программу с единственным изменением что я применяю Math.Round(originalDouble, N) в парном разряде. Поскольку я получаю originalDoubles из случайного класса, все они будут между 0 и 1, поэтому количество значимых цифр совпадает с количеством цифр после десятичной точки. Я поместил этот метод в цикл от 1 значащей цифры до 15 значащих цифр, набранных пользователем. Затем я нарисовал его на графике. Зависимость (сколько раз прямое преобразование лучше, чем преобразование через decimal) от количества значащих цифр, набранных пользователь. .

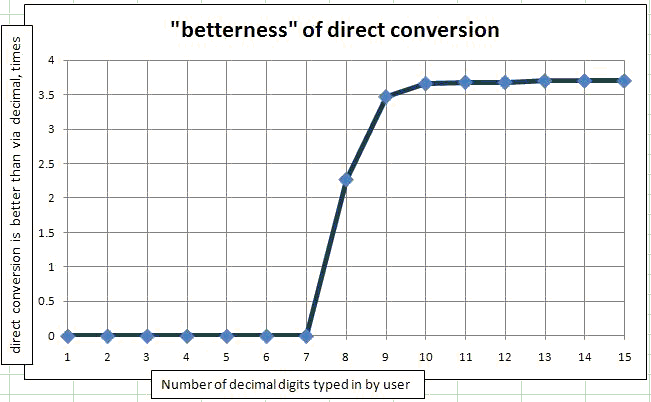как вы можете видеть, для 1 до 7 набранных цифр преобразование через Decimal всегда лучше, чем прямое преобразование. Если быть точным, для миллиона случайных чисел только 1 или 2 не улучшаются путем преобразования в десятичные.

вот код, используемый для сравнения:

private static void CompareWhichIsBetter(int numTypedDigits)
{
    Console.WriteLine("Number of typed digits: " + numTypedDigits);
    Random rnd = new Random(DateTime.Now.Millisecond);
    int countDecimalIsBetter = 0;
    int countDirectIsBetter = 0;
    int countEqual = 0;

    for (int i = 0; i < 1000000; i++)
    {
        double origDouble = rnd.NextDouble();
        //Use the line below for the user-typed-in-numbers case.
        //double origDouble = Math.Round(rnd.NextDouble(), numTypedDigits); 

        float x = (float)origDouble;
        double viaFloatAndDecimal = (double)Convert.ToDecimal(x);
        double viaFloat = x;

        double diff1 = Math.Abs(origDouble - viaFloatAndDecimal);
        double diff2 = Math.Abs(origDouble - viaFloat);

        if (diff1 < diff2)
            countDecimalIsBetter++;
        else if (diff1 > diff2)
            countDirectIsBetter++;
        else
            countEqual++;
    }

    Console.WriteLine("Decimal better: " + countDecimalIsBetter);
    Console.WriteLine("Direct better: " + countDirectIsBetter);
    Console.WriteLine("Equal: " + countEqual);
    Console.WriteLine("Betterness of direct conversion: " + (double)countDirectIsBetter / countDecimalIsBetter);
    Console.WriteLine("Betterness of conv. via decimal: " + (double)countDecimalIsBetter / countDirectIsBetter );
    Console.WriteLine();
}