Кратчайшее расстояние между двумя отрезками линии

Это мое решение в Python. Работает с 3d точек, и вы можете упростить для 2d.

[EDIT 1] я добавил опцию зажима, если вы хотите ограничить результаты сегментами линии

[EDIT 2] Как отметил Д. А., поскольку две линии параллельны, это не означает, что между ними не может быть расстояния. Поэтому я отредактировал код, чтобы справиться с этой ситуацией. Я также сделал условия зажима более общими, поэтому каждый сегмент может быть зажат с любой стороны.

[EDIT 3] адресовано ошибка jhutar указал, что может произойти, когда обе линии зажаты условия и прогнозируемые результаты выходят за пределы сегментов линии.

import numpy as np

def closestDistanceBetweenLines(a0,a1,b0,b1,clampAll=False,clampA0=False,clampA1=False,clampB0=False,clampB1=False):

    ''' Given two lines defined by numpy.array pairs (a0,a1,b0,b1)
        Return the closest points on each segment and their distance
    '''

    # If clampAll=True, set all clamps to True
    if clampAll:
        clampA0=True
        clampA1=True
        clampB0=True
        clampB1=True


    # Calculate denomitator
    A = a1 - a0
    B = b1 - b0
    magA = np.linalg.norm(A)
    magB = np.linalg.norm(B)

    _A = A / magA
    _B = B / magB

    cross = np.cross(_A, _B);
    denom = np.linalg.norm(cross)**2


    # If lines are parallel (denom=0) test if lines overlap.
    # If they don't overlap then there is a closest point solution.
    # If they do overlap, there are infinite closest positions, but there is a closest distance
    if not denom:
        d0 = np.dot(_A,(b0-a0))

        # Overlap only possible with clamping
        if clampA0 or clampA1 or clampB0 or clampB1:
            d1 = np.dot(_A,(b1-a0))

            # Is segment B before A?
            if d0 <= 0 >= d1:
                if clampA0 and clampB1:
                    if np.absolute(d0) < np.absolute(d1):
                        return a0,b0,np.linalg.norm(a0-b0)
                    return a0,b1,np.linalg.norm(a0-b1)


            # Is segment B after A?
            elif d0 >= magA <= d1:
                if clampA1 and clampB0:
                    if np.absolute(d0) < np.absolute(d1):
                        return a1,b0,np.linalg.norm(a1-b0)
                    return a1,b1,np.linalg.norm(a1-b1)


        # Segments overlap, return distance between parallel segments
        return None,None,np.linalg.norm(((d0*_A)+a0)-b0)



    # Lines criss-cross: Calculate the projected closest points
    t = (b0 - a0);
    detA = np.linalg.det([t, _B, cross])
    detB = np.linalg.det([t, _A, cross])

    t0 = detA/denom;
    t1 = detB/denom;

    pA = a0 + (_A * t0) # Projected closest point on segment A
    pB = b0 + (_B * t1) # Projected closest point on segment B


    # Clamp projections
    if clampA0 or clampA1 or clampB0 or clampB1:
        if clampA0 and t0 < 0:
            pA = a0
        elif clampA1 and t0 > magA:
            pA = a1

        if clampB0 and t1 < 0:
            pB = b0
        elif clampB1 and t1 > magB:
            pB = b1

        # Clamp projection A
        if (clampA0 and t0 < 0) or (clampA1 and t0 > magA):
            dot = np.dot(_B,(pA-b0))
            if clampB0 and dot < 0:
                dot = 0
            elif clampB1 and dot > magB:
                dot = magB
            pB = b0 + (_B * dot)

        # Clamp projection B
        if (clampB0 and t1 < 0) or (clampB1 and t1 > magB):
            dot = np.dot(_A,(pB-a0))
            if clampA0 and dot < 0:
                dot = 0
            elif clampA1 and dot > magA:
                dot = magA
            pA = a0 + (_A * dot)


    return pA,pB,np.linalg.norm(pA-pB)

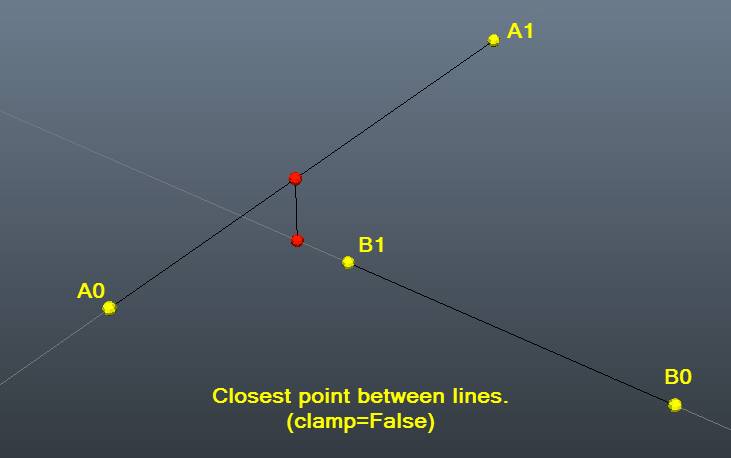
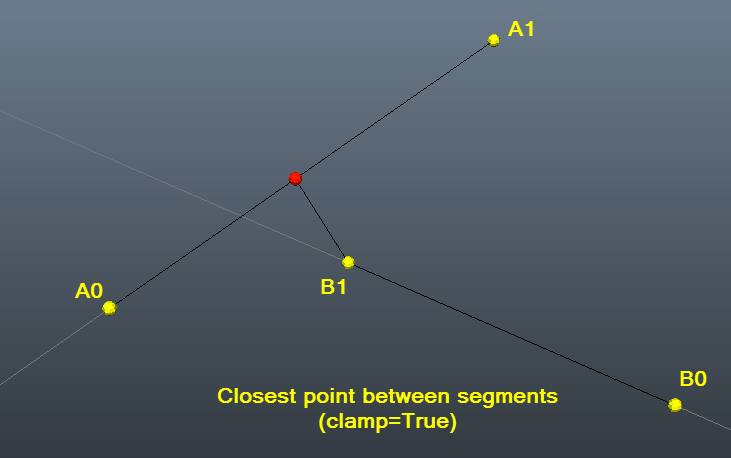
тестовый пример с картинками, чтобы помочь визуализировать:)

a1=np.array([13.43, 21.77, 46.81])
a0=np.array([27.83, 31.74, -26.60])
b0=np.array([77.54, 7.53, 6.22])
b1=np.array([26.99, 12.39, 11.18])

closestDistanceBetweenLines(a0,a1,b0,b1,clampAll=True)
# Result: (15.826771412132246, array([ 19.85163563,  26.21609078,  14.07303667]), array([ 26.99,  12.39,  11.18])) # 
closestDistanceBetweenLines(a0,a1,b0,b1,clampAll=False)
# Result: (13.240709703623203, array([ 19.85163563,  26.21609078,  14.07303667]), array([ 18.40058604,  13.21580716,  12.02279907])) # 

принято от , который также поставляется с простым объяснением того, почему он работает, а также VB-код (это делает больше, чем вам нужно, поэтому я упростил, как я перевел на Python-примечание: Я перевел, но не тестировал, поэтому опечатка могла проскользнуть мимо...):

def segments_distance(x11, y11, x12, y12, x21, y21, x22, y22):
  """ distance between two segments in the plane:
      one segment is (x11, y11) to (x12, y12)
      the other is   (x21, y21) to (x22, y22)
  """
  if segments_intersect(x11, y11, x12, y12, x21, y21, x22, y22): return 0
  # try each of the 4 vertices w/the other segment
  distances = []
  distances.append(point_segment_distance(x11, y11, x21, y21, x22, y22))
  distances.append(point_segment_distance(x12, y12, x21, y21, x22, y22))
  distances.append(point_segment_distance(x21, y21, x11, y11, x12, y12))
  distances.append(point_segment_distance(x22, y22, x11, y11, x12, y12))
  return min(distances)

def segments_intersect(x11, y11, x12, y12, x21, y21, x22, y22):
  """ whether two segments in the plane intersect:
      one segment is (x11, y11) to (x12, y12)
      the other is   (x21, y21) to (x22, y22)
  """
  dx1 = x12 - x11
  dy1 = y12 - y11
  dx2 = x22 - x21
  dy2 = y22 - y21
  delta = dx2 * dy1 - dy2 * dx1
  if delta == 0: return False  # parallel segments
  s = (dx1 * (y21 - y11) + dy1 * (x11 - x21)) / delta
  t = (dx2 * (y11 - y21) + dy2 * (x21 - x11)) / (-delta)
  return (0 <= s <= 1) and (0 <= t <= 1)

import math
def point_segment_distance(px, py, x1, y1, x2, y2):
  dx = x2 - x1
  dy = y2 - y1
  if dx == dy == 0:  # the segment's just a point
    return math.hypot(px - x1, py - y1)

  # Calculate the t that minimizes the distance.
  t = ((px - x1) * dx + (py - y1) * dy) / (dx * dx + dy * dy)

  # See if this represents one of the segment's
  # end points or a point in the middle.
  if t < 0:
    dx = px - x1
    dy = py - y1
  elif t > 1:
    dx = px - x2
    dy = py - y2
  else:
    near_x = x1 + t * dx
    near_y = y1 + t * dy
    dx = px - near_x
    dy = py - near_y

  return math.hypot(dx, dy)

расстояние между линиями и сегментами с их ближайшей точки подхода

для вычисления минимального расстояния между 2 2D сегментами линии верно, что вам нужно выполнить 4 перпендикулярных расстояния от конечной точки до другой линии, последовательно используя каждую из 4 конечных точек. Однако если вы обнаружите, что вытянутая перпендикулярная линия не пересекает сегмент линии ни в одном из 4 случаев, вам нужно выполнить 4 дополнительные проверки расстояния до конечной точки, чтобы найти кратчайшее расстояние.

есть ли более элегантное решение этого я не знаю.

мое решение-это перевод решения Fnord. Я делаю в javascript и C.

В Javascript. Вы должны включить mathjs.

var closestDistanceBetweenLines = function(a0, a1, b0, b1, clampAll, clampA0, clampA1, clampB0, clampB1){
    //Given two lines defined by numpy.array pairs (a0,a1,b0,b1)
    //Return distance, the two closest points, and their average

    clampA0 = clampA0 || false;
    clampA1 = clampA1 || false;
    clampB0 = clampB0 || false;
    clampB1 = clampB1 || false;
    clampAll = clampAll || false;

    if(clampAll){
        clampA0 = true;
        clampA1 = true;
        clampB0 = true;
        clampB1 = true;
    }

    //Calculate denomitator
    var A = math.subtract(a1, a0);
    var B = math.subtract(b1, b0);
    var _A = math.divide(A, math.norm(A))
    var _B = math.divide(B, math.norm(B))
    var cross = math.cross(_A, _B);
    var denom = math.pow(math.norm(cross), 2);

    //If denominator is 0, lines are parallel: Calculate distance with a projection and evaluate clamp edge cases
    if (denom == 0){
        var d0 = math.dot(_A, math.subtract(b0, a0));
        var d = math.norm(math.subtract(math.add(math.multiply(d0, _A), a0), b0));

        //If clamping: the only time we'll get closest points will be when lines don't overlap at all. Find if segments overlap using dot products.
        if(clampA0 || clampA1 || clampB0 || clampB1){
            var d1 = math.dot(_A, math.subtract(b1, a0));

            //Is segment B before A?
            if(d0 <= 0 && 0 >= d1){
                if(clampA0 == true && clampB1 == true){
                    if(math.absolute(d0) < math.absolute(d1)){
                        return [b0, a0, math.norm(math.subtract(b0, a0))];                       
                    }
                    return [b1, a0, math.norm(math.subtract(b1, a0))];
                }
            }
            //Is segment B after A?
            else if(d0 >= math.norm(A) && math.norm(A) <= d1){
                if(clampA1 == true && clampB0 == true){
                    if(math.absolute(d0) < math.absolute(d1)){
                        return [b0, a1, math.norm(math.subtract(b0, a1))];
                    }
                    return [b1, a1, math.norm(math.subtract(b1,a1))];
                }
            }

        }

        //If clamping is off, or segments overlapped, we have infinite results, just return position.
        return [null, null, d];
    }

    //Lines criss-cross: Calculate the dereminent and return points
    var t = math.subtract(b0, a0);
    var det0 = math.det([t, _B, cross]);
    var det1 = math.det([t, _A, cross]);

    var t0 = math.divide(det0, denom);
    var t1 = math.divide(det1, denom);

    var pA = math.add(a0, math.multiply(_A, t0));
    var pB = math.add(b0, math.multiply(_B, t1));

    //Clamp results to line segments if needed
    if(clampA0 || clampA1 || clampB0 || clampB1){

        if(t0 < 0 && clampA0)
            pA = a0;
        else if(t0 > math.norm(A) && clampA1)
            pA = a1;

        if(t1 < 0 && clampB0)
            pB = b0;
        else if(t1 > math.norm(B) && clampB1)
            pB = b1;

    }

    var d = math.norm(math.subtract(pA, pB))

    return [pA, pB, d];
}
//example
var a1=[13.43, 21.77, 46.81];
var a0=[27.83, 31.74, -26.60];
var b0=[77.54, 7.53, 6.22];
var b1=[26.99, 12.39, 11.18];
closestDistanceBetweenLines(a0,a1,b0,b1,true);

в чистом C

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double determinante3(double* a, double* v1, double* v2){
    return a[0] * (v1[1] * v2[2] - v1[2] * v2[1]) + a[1] * (v1[2] * v2[0] - v1[0] * v2[2]) + a[2] * (v1[0] * v2[1] - v1[1] * v2[0]);
}

double* cross3(double* v1, double* v2){
    double* v = (double*)malloc(3 * sizeof(double));
    v[0] = v1[1] * v2[2] - v1[2] * v2[1];
    v[1] = v1[2] * v2[0] - v1[0] * v2[2];
    v[2] = v1[0] * v2[1] - v1[1] * v2[0];
    return v;
}

double dot3(double* v1, double* v2){
    return v1[0] * v2[0] + v1[1] * v2[1] + v1[2] * v2[2];
}

double norma3(double* v1){
    double soma = 0;
    for (int i = 0; i < 3; i++) {
        soma += pow(v1[i], 2);
    }
    return sqrt(soma);
}

double* multiplica3(double* v1, double v){
    double* v2 = (double*)malloc(3 * sizeof(double));
    for (int i = 0; i < 3; i++) {
        v2[i] = v1[i] * v;
    }
    return v2;
}

double* soma3(double* v1, double* v2, int sinal){
    double* v = (double*)malloc(3 * sizeof(double));
    for (int i = 0; i < 3; i++) {
        v[i] = v1[i] + sinal * v2[i];
    }
    return v;
}

Result_distance* closestDistanceBetweenLines(double* a0, double* a1, double* b0, double* b1, int clampAll, int clampA0, int clampA1, int clampB0, int clampB1){
    double denom, det0, det1, t0, t1, d;
    double *A, *B, *_A, *_B, *cross, *t, *pA, *pB;
    Result_distance *rd = (Result_distance *)malloc(sizeof(Result_distance));

    if (clampAll){
        clampA0 = 1;
        clampA1 = 1;
        clampB0 = 1;
        clampB1 = 1;
    }

    A = soma3(a1, a0, -1);
    B = soma3(b1, b0, -1);
    _A = multiplica3(A, 1 / norma3(A));
    _B = multiplica3(B, 1 / norma3(B));
    cross = cross3(_A, _B);
    denom = pow(norma3(cross), 2);

    if (denom == 0){
        double d0 = dot3(_A, soma3(b0, a0, -1));
        d = norma3(soma3(soma3(multiplica3(_A, d0), a0, 1), b0, -1));
        if (clampA0 || clampA1 || clampB0 || clampB1){
            double d1 = dot3(_A, soma3(b1, a0, -1));
            if (d0 <= 0 && 0 >= d1){
                if (clampA0 && clampB1){
                    if (abs(d0) < abs(d1)){
                        rd->pA = b0;
                        rd->pB = a0;
                        rd->d = norma3(soma3(b0, a0, -1));
                    }
                    else{
                        rd->pA = b1;
                        rd->pB = a0;
                        rd->d = norma3(soma3(b1, a0, -1));
                    }
                }
            }
            else if (d0 >= norma3(A) && norma3(A) <= d1){
                if (clampA1 && clampB0){
                    if (abs(d0) <abs(d1)){
                        rd->pA = b0;
                        rd->pB = a1;
                        rd->d = norma3(soma3(b0, a1, -1));
                    }
                    else{
                        rd->pA = b1;
                        rd->pB = a1;
                        rd->d = norma3(soma3(b1, a1, -1));
                    }
                }
            }
        }
        else{
            rd->pA = NULL;
            rd->pB = NULL;
            rd->d = d;
        }
    }
    else{
        t = soma3(b0, a0, -1);
        det0 = determinante3(t, _B, cross);
        det1 = determinante3(t, _A, cross);
        t0 = det0 / denom;
        t1 = det1 / denom;
        pA = soma3(a0, multiplica3(_A, t0), 1);
        pB = soma3(b0, multiplica3(_B, t1), 1);

        if (clampA0 || clampA1 || clampB0 || clampB1){
            if (t0 < 0 && clampA0)
                pA = a0;
            else if (t0 > norma3(A) && clampA1)
                pA = a1;
            if (t1 < 0 && clampB0)
                pB = b0;
            else if (t1 > norma3(B) && clampB1)
                pB = b1;
        }

        d = norma3(soma3(pA, pB, -1));

        rd->pA = pA;
        rd->pB = pB;
        rd->d = d;
    }

    free(A);
    free(B);
    free(cross);
    free(t);
    return rd;
}

int main(void){
    //example
    double a1[] = { 13.43, 21.77, 46.81 };
    double a0[] = { 27.83, 31.74, -26.60 };
    double b0[] = { 77.54, 7.53, 6.22 };
    double b1[] = { 26.99, 12.39, 11.18 };

    Result_distance* rd = closestDistanceBetweenLines(a0, a1, b0, b1, 1, 0, 0, 0, 0);
    printf("pA = [%f, %f, %f]\n", rd->pA[0], rd->pA[1], rd->pA[2]);
    printf("pB = [%f, %f, %f]\n", rd->pB[0], rd->pB[1], rd->pB[2]);
    printf("d = %f\n", rd->d);
    return 0;
}

обратите внимание, что вышеуказанные решения верны в предположении, что отрезки линии не пересекаются! Если отрезки пересекаются, понятно, что их расстояние должно быть 0. Поэтому необходимо провести последнюю проверку: предположим, что расстояние между точкой A и CD, d(A,CD), было наименьшим из 4 проверок, упомянутых Дином. Затем сделайте небольшой шаг вдоль сегмента AB из точки A. обозначьте эту точку E. Если D(E,CD)

это решение, по сути, от Алекса Мартелли, но я добавил класс Point и LineSegment, чтобы облегчить чтение. Я также скорректировал форматирование и добавил некоторые тесты.

пересечение отрезков линии неверно, но, похоже, это не имеет значения для расчета расстояния отрезков линии. Если вас интересует правильное пересечение отрезка линии, посмотрите здесь:как вы определяете, есть ли два сегмента линии интерсект?

#!/usr/bin/env python

"""Calculate the distance between line segments."""

import math


class Point(object):
    """A two dimensional point."""
    def __init__(self, x, y):
        self.x = float(x)
        self.y = float(y)


class LineSegment(object):
    """A line segment in a two dimensional space."""
    def __init__(self, p1, p2):
        assert isinstance(p1, Point), \
            "p1 is not of type Point, but of %r" % type(p1)
        assert isinstance(p2, Point), \
            "p2 is not of type Point, but of %r" % type(p2)
        self.p1 = p1
        self.p2 = p2


def segments_distance(segment1, segment2):
    """Calculate the distance between two line segments in the plane.

    >>> a = LineSegment(Point(1,0), Point(2,0))
    >>> b = LineSegment(Point(0,1), Point(0,2))
    >>> "%0.2f" % segments_distance(a, b)
    '1.41'
    >>> c = LineSegment(Point(0,0), Point(5,5))
    >>> d = LineSegment(Point(2,2), Point(4,4))
    >>> e = LineSegment(Point(2,2), Point(7,7))
    >>> "%0.2f" % segments_distance(c, d)
    '0.00'
    >>> "%0.2f" % segments_distance(c, e)
    '0.00'
    """
    if segments_intersect(segment1, segment2):
        return 0
    # try each of the 4 vertices w/the other segment
    distances = []
    distances.append(point_segment_distance(segment1.p1, segment2))
    distances.append(point_segment_distance(segment1.p2, segment2))
    distances.append(point_segment_distance(segment2.p1, segment1))
    distances.append(point_segment_distance(segment2.p2, segment1))
    return min(distances)


def segments_intersect(segment1, segment2):
    """Check if two line segments in the plane intersect.
    >>> segments_intersect(LineSegment(Point(0,0), Point(1,0)), \
                           LineSegment(Point(0,0), Point(1,0)))
    True
    """
    dx1 = segment1.p2.x - segment1.p1.x
    dy1 = segment1.p2.y - segment1.p2.y
    dx2 = segment2.p2.x - segment2.p1.x
    dy2 = segment2.p2.y - segment2.p1.y
    delta = dx2 * dy1 - dy2 * dx1
    if delta == 0:  # parallel segments
        # TODO: Could be (partially) identical!
        return False
    s = (dx1 * (segment2.p1.y - segment1.p1.y) +
         dy1 * (segment1.p1.x - segment2.p1.x)) / delta
    t = (dx2 * (segment1.p1.y - segment2.p1.y) +
         dy2 * (segment2.p1.x - segment1.p1.x)) / (-delta)
    return (0 <= s <= 1) and (0 <= t <= 1)


def point_segment_distance(point, segment):
    """
    >>> a = LineSegment(Point(1,0), Point(2,0))
    >>> b = LineSegment(Point(2,0), Point(0,2))
    >>> point_segment_distance(Point(0,0), a)
    1.0
    >>> "%0.2f" % point_segment_distance(Point(0,0), b)
    '1.41'
    """
    assert isinstance(point, Point), \
        "point is not of type Point, but of %r" % type(point)
    dx = segment.p2.x - segment.p1.x
    dy = segment.p2.y - segment.p1.y
    if dx == dy == 0:  # the segment's just a point
        return math.hypot(point.x - segment.p1.x, point.y - segment.p1.y)

    if dx == 0:
        if (point.y <= segment.p1.y or point.y <= segment.p2.y) and \
           (point.y >= segment.p2.y or point.y >= segment.p2.y):
            return abs(point.x - segment.p1.x)

    if dy == 0:
        if (point.x <= segment.p1.x or point.x <= segment.p2.x) and \
           (point.x >= segment.p2.x or point.x >= segment.p2.x):
            return abs(point.y - segment.p1.y)

    # Calculate the t that minimizes the distance.
    t = ((point.x - segment.p1.x) * dx + (point.y - segment.p1.y) * dy) / \
        (dx * dx + dy * dy)

    # See if this represents one of the segment's
    # end points or a point in the middle.
    if t < 0:
        dx = point.x - segment.p1.x
        dy = point.y - segment.p1.y
    elif t > 1:
        dx = point.x - segment.p2.x
        dy = point.y - segment.p2.y
    else:
        near_x = segment.p1.x + t * dx
        near_y = segment.p1.y + t * dy
        dx = point.x - near_x
        dy = point.y - near_y

    return math.hypot(dx, dy)

if __name__ == '__main__':
    import doctest
    doctest.testmod()

все 2D-линии, если они не параллельны, в конечном итоге встретятся. Узнайте, чему вас учат, чтобы понять это, а не пытаться обмануть этот конкретный q.