Кратчайший путь на графике, где расстояния изменяются динамически? (максимальный путь энергии )
Я пытаюсь найти кратчайший путь между двумя максимумами на дискретном энергетическом ландшафте, где кратчайший путь-это то, что уменьшает наименьшую высоту в течение всего пути. Вероятно, путь максимальной энергии-более правильная терминология, но другими словами, даже если путь проходит большое расстояние по ландшафту, но не спускается в долины, это будет считаться хорошим.
моей первоначальной идеей было создать график ландшафта при этом вес был разницей в высоте ландшафта между соседями, либо положительной, либо отрицательной для подъема и спуска соответственно. Я только что понял, что это не даст нужного мне результата, и на самом деле все пути между локальными максимумами будут иметь точно такую же стоимость.
Я понял, что если расстояние между узлами на этом графике зависит от текущего положения и истории путь, тогда я мог бы получить результат, который мне нужен. например, если путь пошел вниз, и вверх из долины, то я бы назначать без дополнительной платы спускаясь другую долину (пока путь не превышает минимумы не были).
Итак, существуют ли алгоритмы поиска графов, где расстояние может динамически меняться по мере изучения путей?
или есть какие-либо другие предложения для нападения на эту проблему?
6 ответов
Это известно как проблема кратчайшего пути узкого места. На самом деле это проще, чем задача кратчайшего пути, и может быть решена в линейное время на неориентированных графах. См., например,здесь.
идея
Я предлагаю алгоритм, который строит вспомогательное дерево (T), в котором каждый узел содержит список вершин. Каждое поддерево будет содержать набор вершин, которые отделены от остальной части графа по долине. Чтобы найти расстояние между любыми двумя узлами, нужно просто найти их наименьшего общего предка в дереве.
алгоритм
инициализации:
- сортировка вершин по высоте (пробел:
O(V)время:O(V log V)) - пусть T состоит только из корневого узла
r
MakeTree(G, r):
- возьмите самую низкую вершину в графе
G, удалите его из графика и добавьте в список в корнеr(затраты времени на вершину:O(1 + E/V)) - повторите вышеуказанный шаг, пока график подключен
- для каждого подключенного компонента
G'графикаG:- создать новый узел
nв T присоедините узел как дочерний элемент корня - рекурсивно запустить
MakeTree(G', n)
- создать новый узел
теперь у вас есть дерево с таким свойством, что если вы хотите отправиться из вершины A to B, ваш максимальный энергетический путь будет вести через самую высокую из вершин, хранящихся в самом низком общем предке A и B. Чтобы найти расстояние, просто найдите наименьшего общего предка и возьмите самую высокую вершину C хранится там и вычислить max(abs(h(A) - h(C)), abs(h(B) - h(C))).
пример
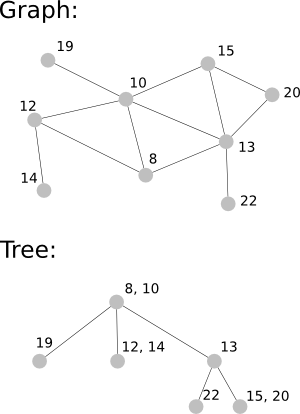
Ниже приведен пример графа и соответствующего дерева (для краткости метки вершин-это их высоты). Например, если вы хотите перейти от 22 к 14, вам нужно пройти через 10 (самая высокая вершина в самом низком общем предке в дереве, расстояние = 22-10). Если вы хотите пройти от 22 до 20, вы должны пройти через 13 (расстояние = 22-13).
возможно, следующие работы:
создайте график ландшафта с весами, равными dist + abs (height_a - height_b).
функция abs делает его дорогим для подъема или падения, и, как вы уже заметили, разница в высоте сама по себе недостаточно, так как она постоянна для любой две точки На карте независимо от того, какой маршрут вы идете.
dist-это простое расстояние (или даже Константа 1 во всех случаях) и может быть опущена, но если вам нравится чтобы получить короче пути это должно благоприятствовать коротким по сравнению с длинными с другими же затратами.
Это непроверено, конечно. :-)
учитывая, что конечные точки находятся в максимумах, ваша проблема эквивалентна этой:
для x на графике пусть H (x) - расстояние ниже начальной точки. (По постановке задачи все точки находятся ниже начальной точки).
найдите путь, который минимизирует: max(h (x) для x в пути).
вы можете использовать вариант кратчайшего пути Dijkstra для решения этой проблемы. Я скопировал и изменил описание алгоритма из Википедии (только расстояние расчет на Шаге 3 изменения).
назначьте каждому узлу значение расстояния. Установите его равным нулю для нашего начального узла и бесконечности для всех других узлов.
пометить все узлы как не посещенные. Задайте начальный узел как текущий.
для текущего узла рассмотрите всех его неявленных соседей и вычислите их предварительное расстояние (от начального узла). Например, если текущий узел (A) имеет расстояние 6 и подключен к другой узел (B) С h(B) = 7, расстояние до B через A будет max(6, 7) = 7. Если это расстояние меньше ранее записанного расстояния (бесконечность в начале, ноль для начального узла), перепишите расстояние.
когда мы закончим рассмотрение всех соседей текущего узла, отметьте его как посещенный. Посещенный узел больше не будет проверяться; его расстояние, записанное сейчас, является окончательным и минимальным. Если все узлы были посещены, отделка. В противном случае установите непосещенных узлов с наименьшего расстояния (от начального узла) в качестве следующего "текущий узел" и продолжите с шага 3.
таким образом, вас совсем не волнует общая длина пути, верно? Только минимальное значение, которое вы встретите на пути?
Если это так, то вы не должны использовать "расстояние" в традиционном смысле в качестве стоимости для Dijkstra. Ваша очередь приоритетов должна возвращать узел с наибольшим значением энергии - таким образом, Вы гарантированно никогда не пройдете путь через меньшее значение, если существует лучший путь.
Я считаю, что это отличается от того, что @Paul Hankin предполагая в своем ответе. Это, вероятно, откроет много узлов на графике; я думаю, вы можете оптимизировать следующим образом:
используйте [Евклидово или манхэттенское] расстояние до цели в качестве связующего звена в функции сравнения. Таким образом, если два узла имеют одинаковую энергию, вы попробуете тот, который быстрее доберется до цели.
при добавлении узлов в очередь приоритетов вместо того, чтобы использовать ее фактическую энергию для ее "стоимости", используйте минимум ее энергии и наименьшей энергии до сих пор. Поскольку вы заботитесь только о глобальной минимальной стоимости, как только вы вынуждены взять низкоэнергетический узел, все выше этого "стоит" то же самое. Это заставляет поиск вести себя как обычный поиск A* в окрестности цели.
запуск поиска в нижней части локальных максимумов (я не уверен, но думаю, что это будет быстрее).
используя расстояние как tie-breaker в #1 не повлияет на минимальная энергия, но она должна заставить вещи работать быстрее (это похоже на поиск A*).
Edit: вот совершенно другой (но, вероятно, более медленный) способ думать.
Сначала выберите пороговую энергию. Выполните стандартный поиск Dijkstra/A*, но отклоните все узлы, энергия которых ниже порога. Если у вас нет пути, выберите больший порог и повторите попытку. "Безопасным" первоначальным предположением будет минимальное E по простому пути (например, идти налево затем вверх) от начала до цели.
теперь увеличьте порог и повторите Dijkstra / A*. Продолжайте делать это, пока не сможете найти путь. Последний путь перед тем, как вы больше не можете найти путь, - это кратчайший путь, который имеет наибольшую минимальную энергию вдоль пути.
вы также можете повторно использовать стоимость пути из одного поиска в качестве улучшенной эвристики a* для следующего поиска. Поскольку увеличение порога приведет только к увеличению длины путей, это допустимая эвристика.
надеюсь, это поможет. Дайте мне знать, если что-то непонятно.
две возможности.
a), например, в версии at http://en.wikipedia.org/wiki/Dijkstra%27s_algorithm существует линия, которая разрабатывает возможно улучшенное расстояние до точки v, используя маршрут через точку u:
alt: = dist[u] + dist_between (u, v)
14 если alt
15 dist[v]: = alt
16 предыдущий[v]: = u
Вы, кажется, хотите версию, которая идет alt: = K-min (высота[u], высота[v]). Это работает по той же причине, что и версия с добавлением: в любое время множество вершин, удаленных из Q, имеют минимальную стоимость, правильно разработанную для любого маршрута от источника. Каждый раз, когда вы удаляете вершину из Q, потому что вы удаляете ее с минимальным расстоянием, нет никаких шансов на короткий путь к ней, используя другие вершины все еще в Q.
b) примите любой метод для выясняем, есть ли вообще маршрут от источника. Используйте график, который содержит только точку с высотой >= H и посмотрите, есть ли решение. Попробуйте различные H, пока не найдете тот, который просто работает. Вы можете отсортировать все высоты заранее, а затем использовать двоичный ЧОП для этого массива.
