кривые Безье n-го порядка?
мне удалось реализовать квадратичные и кубические кривые Безье.Они довольно просты, так как у нас есть формула. Теперь я хочу представить кривую Безье n-го порядка, используя обобщение:
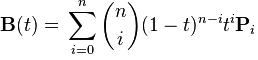
здесь
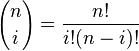
и
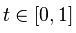
Я использую библиотеку растровых изображений для отображения вывода, поэтому вот мой код:
// binomialCoef(n, k) = (factorial(n) / (factorial(k) * factorial(n- k)))
unsigned int binomialCoef(unsigned int n, const unsigned int k)
{
unsigned int r = 1;
if(k > n)
return 0;
for(unsigned int d = 1; d <= k; d++)
{
r *= n--;
r /= d;
}
return r;
}
void nBezierCurve(Bitmap* obj, const Point* p, const unsigned int nbPoint, float steps, const unsigned char red, const unsigned char green, const unsigned char blue)
{
int bx1 = p[0].x;
int by1 = p[0].y;
int bx2;
int by2;
steps = 1 / steps;
for(float i = 0; i < 1; i += steps)
{
bx2 = by2 = 0;
for(int j = 0; (unsigned int)j < nbPoint; j++)
{
bx2 += (int)(binomialCoef(nbPoint, j) * pow(1 - i, (float)nbPoint - j) * pow(i, j) * p[j].x);
by2 += (int)(binomialCoef(nbPoint, j) * pow(1 - i, (float)nbPoint - j) * pow(i, j) * p[j].y);
}
bresenhamLine(obj, bx1, by1, bx2, by2, red, green, blue);
bx1 = bx2;
by1 = by2;
}
// curve must end on the last anchor point
bresenhamLine(obj, bx1, by1, p[nbPoint - 1].x, p[nbPoint - 1].y, red, green, blue);
}
вот набор точек для рендер:
Point ncurv[] = {
20, 200,
70, 300,
200, 400,
250, 200
};
и вот вывод:
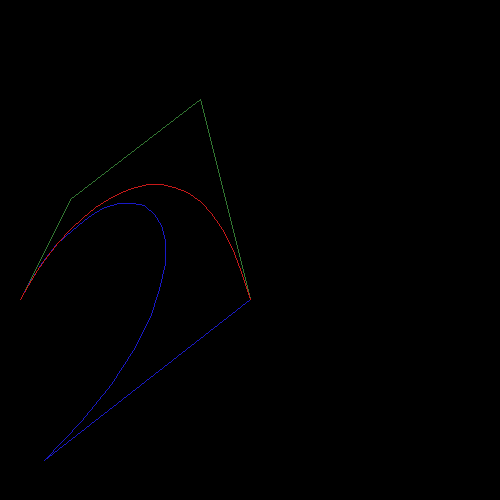
красная кривая Безье. Синий должен быть Безье 4-го порядка, который совпадает с кубическим Безье, но в этом случае они не одинаковы ?!
EDIT: Я забыл отметить, что нижняя левая точка (0, 0)
2 ответов
сумма в Формуле...
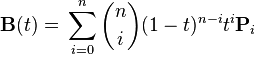
...работает от 0 до n, т. е. для n-го порядка Безье нужно N+1 точек.
у вас есть 4 очка, поэтому вы рисуете Безье 3-го порядка.
ошибка в вашем коде здесь:
for(int j = 0; (unsigned int)j < nbPoint; j++)
должно быть:
for(int j = 0; (unsigned int)j <= nbPoint; j++)
в противном случае вы только повторяете от 0 до n-1.
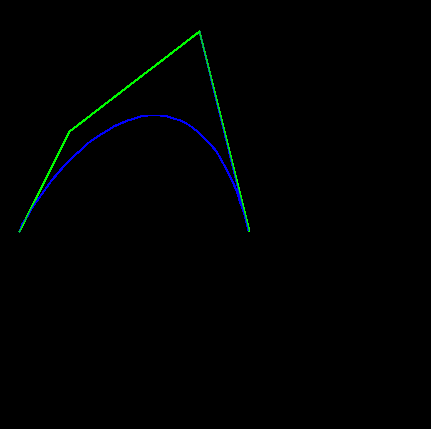
EDIT:
из интереса, форма, которую вы получали это то же самое, как если бы отсутствующая (5-я) точка была на (0,0), так как это единственная точка, которая ничего не внесет в вашу сумму...
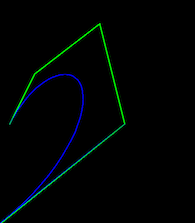
вы пытаетесь построить кривую Безье 4-го порядка только на четырех точках. Неудивительно, что он не работает.
