Кубический сплайн-метод для данных продольных рядов?
у меня есть последовательные данные, отформатированные следующим образом:
time milk Animal_ID
30 25.6 1
31 27.2 1
32 24.4 1
33 17.4 1
34 33.6 1
35 25.4 1
33 29.4 2
34 25.4 2
35 24.7 2
36 27.4 2
37 22.4 2
80 24.6 3
81 24.5 3
82 23.5 3
83 25.5 3
84 24.4 3
85 23.4 3
. . .
вообще, 300 животных имеют показатели молока в различных пунктах времени короткого периода. Однако, если мы объединим их данные вместе и не будем заботиться о разных animal_ID, у нас будет кривая между milk~time, как это, линия на рисунке ниже:
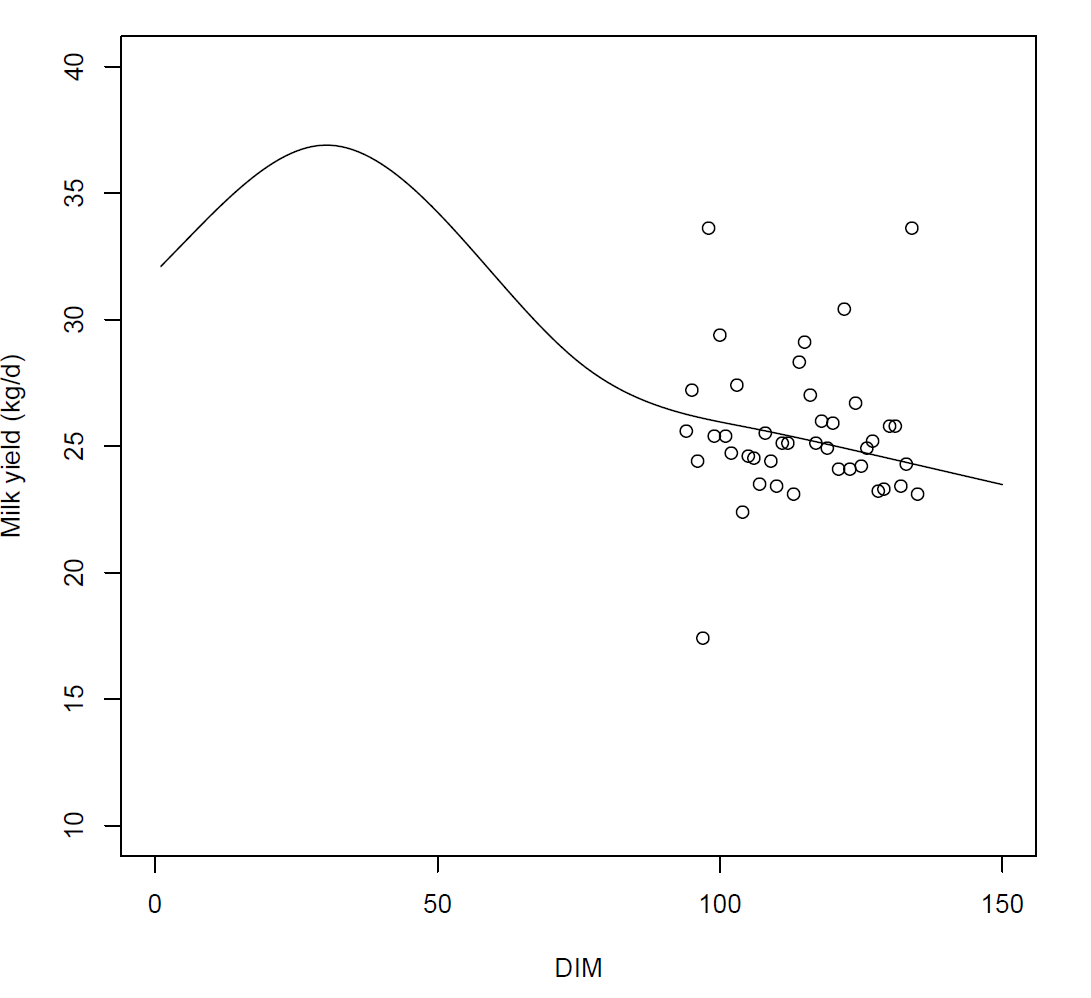 Кроме того, на приведенном выше рисунке у нас есть данные для 1 примера животных, они короткие и сильно изменчивые. Моя цель-сгладить данные каждого животного, но это было бы, если бы модель позволяла изучать общую скороговорку из целых данных. Я использовал другую гладкую модель (ns, bs, smooth.spline) со следующим форматом, но он просто не работал:
Кроме того, на приведенном выше рисунке у нас есть данные для 1 примера животных, они короткие и сильно изменчивые. Моя цель-сгладить данные каждого животного, но это было бы, если бы модель позволяла изучать общую скороговорку из целых данных. Я использовал другую гладкую модель (ns, bs, smooth.spline) со следующим форматом, но он просто не работал:
mod <- lme(milk ~ bs(time, df=3), data=dat, random = ~1|Animal_ID)
Я надеюсь, что если кто-то уже занимался этой проблемой, даст мне совет. Спасибо Полный набор данных можно получить отсюда: https://www.dropbox.com/s/z9b5teh3su87uu7/dat.txt?dl=0
1 ответов
я бы предложил вам использовать mgcv пакета. Это один из рекомендуемых пакетов R, выполняющий класс моделей под названием обобщенные аддитивные смешанные модели. Вы можете просто загрузить его library(mgcv). Это очень мощная библиотека, которая может обрабатывать от простейшей модели линейной регрессии до обобщенных линейных моделей, аддитивных моделей, обобщенных аддитивных моделей, а также моделей со смешанными эффектами (фиксированные эффекты + случайные эффекты). Вы можете перечислить все (экспортированные) функции mgcv via
ls("package:mgcv")
и вы можете видеть, что их много.
для ваших конкретных данных, вы можете использовать модель с формулой:
model <- milk ~ s(time, bs = 'cr', k = 100) + s(Animal_ID, bs = 're')
на mgcv, s() - это настройка для гладких функций, представленная основой сплайна, подразумеваемой bs. "cr" - это кубический сплайн-базис, который является именно тем, что вы хотите. k - число узлов. Его следует выбирать в зависимости от количества уникальных значений переменной time в набор данных. Если вы установите k именно для этого числа вы получаете сглаживающий сплайн; в то время как любое значение меньше этого означает сплайн регрессии. Однако оба будут наказаны (если вы знаете, что означает наказание). Я прочитал ваши данные в:
dat <- na.omit(read.csv("data.txt", header = TRUE)) ## I saved you data into file "data.txt"
dat$Animal_ID <- factor(dat$Animal_ID)
nrow(dat) ## 12624 observations
length(unique(dat$time)) ## 157 unique time points
length(ID <- levels(dat$Animal_ID)) ## 355 cows
есть 157 уникальных значений, поэтому я считаю k = 100 это, возможно, уместно.
For Animal_ID (принужденный как фактор), нам нужен модельный термин для случайного эффекта. "re" - это особый класс для i.Я. d случайный эффект. Он передается bs по какой-то внутренней причине построения матрицы (так что это не гладкая функция!).
теперь, чтобы соответствовать модели GAM, вы можете вызвать legacy gam или постоянно развивающемся bam (gam для больших данных). Я думаю, вы воспользуетесь последним. У них одно и то же соглашение о вызове, подобное lm и glm. Например, вы можете сделать:
fit <- bam(model, data = dat, family = "gaussian", discrete = TRUE, nthreads = 2)
Как видите, bam позволяет многоядерных параллельных вычислений через nthreads. В то время как discrete заново начатая особенность которая может быстро пройти вверх по образованию матрицы.
поскольку вы имеете дело с данными временных рядов, наконец, вы можете рассмотреть некоторую временную автокорреляцию. mgcv позволяет конфигурировать корреляцию AR1, коэффициент корреляции которой передается bam аргумент rho. Однако вам нужен дополнительный индекс AR_start рассказать mgcv как временной ряд распадается на части. Например, при достижении другого Animal_ID, AR_start получить TRUE для указания нового сегмента временных рядов. См.?bam для сведения.
mgcv предоставляет
-
summary.gamфункция для модельного резюме -
gam.checkдля проверки базовой модели -
plot.gamфункция для построения отдельных терминов -
predict.gam(илиpredict.bam) для прогнозирования по новым данным.
например, резюме предложенной выше модели есть:
> summary(fit)
Family: gaussian
Link function: identity
Formula:
milk ~ s(time, bs = "cr", k = 100) + s(Animal_ID, bs = "re")
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 26.1950 0.2704 96.89 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(time) 10.81 13.67 5.908 1.99e-11 ***
s(Animal_ID) 351.43 354.00 136.449 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
R-sq.(adj) = 0.805 Deviance explained = 81.1%
fREML = 29643 Scale est. = 5.5681 n = 12624
The edf (степени свободы) может рассматриваться как мера степени нелинейности. Поэтому мы вставляем k = 100, а закончилось edf = 10.81. это предполагает, что сплайн s(time) был сильно наказан. вы можете просмотреть что s(time) похоже на:
plot.gam(fit, page = 1)
обратите внимание, что случайный эффект s(Animal_ID) также имеет "гладкую", то есть коровью константу. Для случайных эффектов гауссовский QQ-график будет возвращенный.
диагностические цифры, возвращенные
invisible(gam.check(fit))
выглядит нормально, поэтому я думаю, что модель приемлема (я не предлагаю вам выбор модели, поэтому придумайте лучшую модель, если вы думаете, что есть).
если вы хотите сделать прогноз на матч Animal_ID = 26, вы можете сделать
newd <- data.frame(time = 1:150, Animal_ID = 26)
oo <- predict.gam(fit, newd, type = `link`, se.fit = TRUE)
обратите внимание, что
- вам нужно включить обе переменные в
newd(иначеmgcvжалуется на отсутствие переменной) - с у вас есть только один сплайн-гладкая
s(time), и термин случайный эффектs(Animal_ID)является константой perAnimal_ID. так что это нормально использоватьtype = 'link'для индивидуального прогноза. Кстати,type = 'terms'медленнее, чемtype = 'link'.
если вы хотите сделать прогноз для более чем одной коровы, попробуйте что-то вроде этого:
pred.ID <- ID[1:10] ## predict first 10 cows
newd <- data.frame (time = rep (1:150, times = n), Animal_ID = factor (rep (pred.ID, each = 150)))
oo <- predict.bam (fit, newd, type = "link", se.fit = TRUE)
обратите внимание, что
- я использовал
predict.bamздесь, как сейчас у нас150 * 10 = 1500точки данных для прогнозирования. Плюс: мы требуемse.fit = TRUE. Это довольно дорого, поэтому используйтеpredict.bamбыстрееpredict.gam. В частности, если вы установили свою модель, используяbam(..., discrete = TRUE), можноpredict.bam(..., discrete = TRUE). Процесс прогнозирования проходит те же этапы формирования матрицы, что и при подгонке модели (см.?smoothConиспользованный в модельном штуцере и?PredictMatиспользуется в прогнозировании, если вы хотите узнать больше внутренней структурыmgcv.) - я
Animal_IDкак факторы, потому что это случайный эффект.
дополнительные on mgcv, вы можете обратиться к руководству библиотеки. Проверьте специально ?mgcv, ?gam, ?bam ?s.
последнее обновление
хотя я сказал, что не буду помогать вам с разделом модели, но я думаю, что эта модель лучше (она дает выше adj-Rsquared) и также более разумно в смысле:
model <- milk ~ s(time, bs = 'cr', k = 20) + s(Animal_ID, bs = 're') + s(Animal_ID, time, bs = 're')
последний термин вводит случайные помои. Это означает, что мы предполагаем, что каждого человека корова имеет различную картину выращивания / сокращения производства молока. Это более разумное предположение в вашей проблеме. Более ранней модели со случайным перехватом недостаточно. После добавления этой случайной помои гладкий термин s(time) выглядит более гладкой. Это хороший знак, а не плохой знак, потому что нам нужно какое-то простое объяснение s(time), не так ли? Сравните s(time) вы получаете от обеих моделей, и посмотреть, что вы обнаружите.
я также уменьшил k = 100 to k = 20. Как мы видели в предыдущем fit,edf для этого термина около 10, так что k = 20 вполне достаточно.
