Либо f (n) = O(g (n)), либо g (n) = O (f(n))
Я пытаюсь доказать, что это правильно для любой функции f и g с доменом и co-доменом N. Я видел, что это доказано с использованием пределов, но, по-видимому, вы также можете доказать это без них.
по существу, я пытаюсь доказать, что " если f(n) не имеет большого-O из g(n), то g(n) должен иметь большое-O из f (n). У меня проблема в том, что я пытаюсь понять, что означает "f не имеет большой буквы g".
согласно формальному определению big-O, если f( n) = O (g(n)) тогда n>=N - > f(n)
2 ответов
не правда. Пусть f(n) = 1 Если n нечетно, и нулю в противном случае, и g(n) = 1 Если n еще и ноль в противном случае.
говорил, что f is O(g) сказал бы, что есть константа C > 0 и N > 0 такое, что n > N подразумевает f(n) <= C g(n). Пусть n = 2 * N + 1, так что n - это странно. Тогда f(n) = 1 но g(n) = 0, так что f(n) <= C * g(n) - это невозможно. Таким образом, f is O(g) - это неправда.
аналогично, мы можем показать, что g и O(f) не истинный.
прежде всего, ваше определение big-O-это мало Битт выкл. Ты говоришь:
я думаю, что это означает, что нет c, который выполняет это неравенство для всех значений n.
на самом деле, вам нужно выбрать значение c, которые удовлетворяют неравенству любой стоимостью n.
в любом случае, чтобы ответить на вопрос:
я не верю, что утверждение в вопросе истинно... Давайте посмотрим, можем ли мы придумать встречный пример, где f(n) ≠ O(g(n)) и g(n) ≠ O(f(n)).
примечание: Я буду использовать n и x взаимозаменяемо, так как мне легче так думать.
мы должны были бы придумать две функции, которые постоянно пересекаются друг с другом по мере их продвижения к бесконечности. Не только это, но они должны были бы продолжать пересекать друг друга независимо от константы c что мы multibly их.
так это заставляет меня думать, что функции должны будут чередоваться между двумя различными сложностями времени.
давайте посмотрим на функцию, которая чередуется междуy = x и y = x^2:
f(x) = .2 (x * sin(x) + x^2 * (1 - sin(x)) )
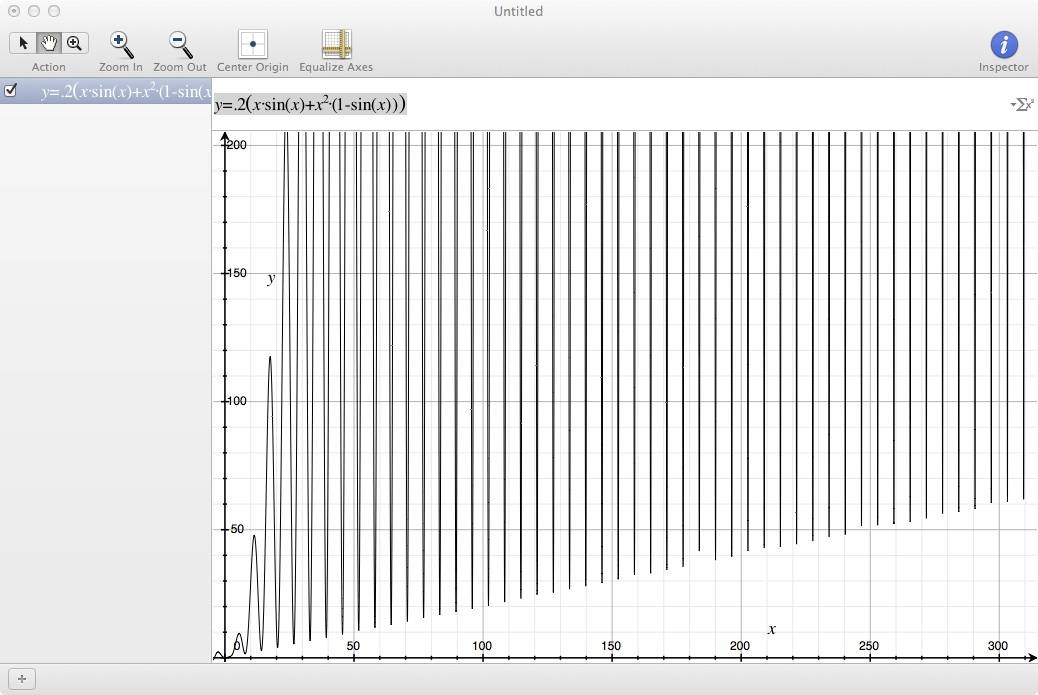
теперь, если мы создадим аналогичную функцию со слегка смещенным колебанием:
g(x) = .2 (x * cos(x) + x^2 * (1 - cos(x)) )
тогда эти две функции будут продолжать пересекать пути друг друга до бесконечности.
для любого числа N что вы выберите, независимо от того, как высоко, будет x1 больше N такое, что f(x) = x^2 и g(x) = x. Аналогично, будет x2 такое, что g(x) = x^2 и f(x) = x.
в эти моменты вы не сможете выбрать любой c1 или c2 это гарантирует, что f(x) < c1 * g(x) или g(x) < c2 * f(x).
в заключение, f(n) ≠ O(g(n)) не означает g(n) = O(f (n)).
