Линейная Регрессия: Нормализация (Vs) Стандартизация
Я использую линейную регрессию для прогнозирования данных. Но я получаю совершенно противоположные результаты, когда нормализую (Vs) стандартизированные переменные.
нормализация = х -х минутам/ а xmax – х минутам Стандартизация нулевого балла = x-xmean/ xstd
a) Also, when to Normalize (Vs) Standardize ?
b) How Normalization affects Linear Regression?
c) Is it okay if I don't normalize all the attributes/lables in the linear regression?
спасибо, Сантош!--2-->
2 ответов
обратите внимание, что результаты могут не обязательно быть самые разные. Возможно, Вам просто понадобятся разные гиперпараметры для двух вариантов, чтобы дать похожие результаты.
идеальная вещь-проверить, что лучше всего подходит для вашей проблемы. Если по какой-то причине вы не можете себе этого позволить, большинство алгоритмов, вероятно, выиграют от стандартизации больше, чем от нормализации.
посмотреть здесь для некоторых примеров когда одно должно быть предпочтено над другое:
например, при анализе кластеризации стандартизация может иметь особенно важное значение для сравнения сходства между объектами на основе определенных показателей расстояния. Другим ярким примером является анализ главных компонентов, где мы обычно предпочитаем стандартизацию масштабированию Min-Max, поскольку нас интересуют компоненты, которые максимизируют дисперсию (в зависимости от вопроса и если PCA вычисляет компоненты через корреляционную матрицу вместо ковариационная Матрица; Но больше о PCA в моей предыдущей статье).
однако это не означает, что масштабирование Min-Max вообще не полезно! Популярным приложением является обработка изображений, где интенсивность пикселей должна быть нормализована, чтобы соответствовать определенному диапазону (т. е. от 0 до 255 для цветового диапазона RGB). Кроме того, типичный алгоритм нейронной сети требует данных в масштабе 0-1.
одним из недостатков нормализации по сравнению со стандартизацией является то, что она теряет некоторые информация в данных, особенно о выбросах.
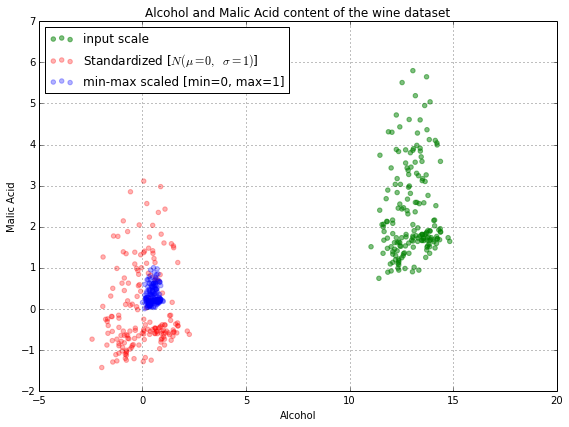
также на связанной странице есть это изображение:
Как вы можете видеть, масштабирование кластеров все данные очень близко друг к другу, что может быть не то, что вы хотите. Это может привести к тому, что такие алгоритмы, как градиентный спуск, будут дольше сходиться к тому же решению, что и в стандартизированном наборе данных, или даже сделать это невозможным.
"нормализации переменных" в этом нет никакого смысла. Правильная терминология - "нормализация / масштабирование функций". Если вы собираетесь нормализовать или масштабировать одну функцию, вы должны сделать то же самое для остальных.
Это имеет смысл, потому что нормализация и стандартизация делают разные вещи.
нормализация преобразует ваши данные в диапазон от 0 до 1
стандартизация преобразует ваши данные таким образом, что результирующее распределение имеет среднее значение 0 и стандартное отклонение 1
нормализация / стандартизация предназначены для достижения аналогичной цели, которая заключается в создании функций, имеющих одинаковые диапазоны друг для друга. Мы хотим этого, чтобы быть уверенными, что мы ... захватывают истинную информацию в объекте, и что мы не перевешиваем конкретный объект только потому, что его значения намного больше, чем другие объекты.
Если все ваши функции находятся в одинаковом диапазоне друг от друга, то нет реальной необходимости стандартизировать/нормализовать. Если, однако, некоторые функции естественным образом принимают значения, которые намного больше/меньше других, то нормализация / стандартизация требуется
Если вы собираетесь нормализовать хотя бы один переменная / функция, я бы сделал то же самое со всеми остальными, а также