Любой способ решить систему связанных дифференциальных уравнений в python?

Я работал с sympy и scipy, но не могу найти или выяснить, как решить систему связанных дифференциальных уравнений (нелинейных, первого порядка).

Итак, есть ли способ решить связанные дифференциальные уравнения?

уравнения имеют вид:

V11'(s) = -12*v12(s)**2
v22'(s) = 12*v12(s)**2
v12'(s) = 6*v11(s)*v12(s) - 6*v12(s)*v22(s) - 36*v12(s)

с начальными условиями для v11(s), v22(s), v12 (s).

14
enthought numpy python scipy sympy

2 ответов

для численного решения оду с помощью scipy см. функцию scipy.интегрировать.odeint или класс scipy.интегрировать.ода!--2-->.

некоторые примеры приведены в Составляющей Поваренной (прокрутите вниз до раздела "обыкновенные дифференциальные уравнения").

12

в дополнение к методам SciPy odeint и ode что уже упоминалось, теперь имеет solve_ivp что является более новым и часто более удобным. Полный пример, кодировка [v11, v22, v12] в массиве v: 

from scipy.integrate import solve_ivp
def rhs(s, v): 
    return [-12*v[2]**2, 12*v[2]**2, 6*v[0]*v[2] - 6*v[2]*v[1] - 36*v[2]]
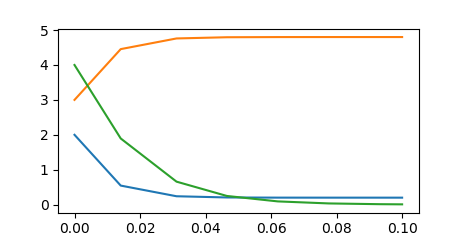
res = solve_ivp(rhs, (0, 0.1), [2, 3, 4])

это решает систему на интервале (0, 0.1) С начальной стоимостью [2, 3, 4]. Результат имеет независимую переменную (s в вашей нотации) как res.t: 

array([ 0.        ,  0.01410735,  0.03114023,  0.04650042,  0.06204205,
        0.07758368,  0.0931253 ,  0.1       ])

эти значения были выбраны автоматически. Можно обеспечить t_eval чтобы решение оценивалось в нужных точках: например, t_eval=np.linspace(0, 0.1).

зависимая переменная (функция, которую мы ищем) в res.y: 

array([[ 2.        ,  0.54560138,  0.2400736 ,  0.20555144,  0.2006393 ,
         0.19995753,  0.1998629 ,  0.1998538 ],
       [ 3.        ,  4.45439862,  4.7599264 ,  4.79444856,  4.7993607 ,
         4.80004247,  4.8001371 ,  4.8001462 ],
       [ 4.        ,  1.89500744,  0.65818761,  0.24868116,  0.09268216,
         0.0345318 ,  0.01286543,  0.00830872]])

С Matplotlib это решение строится как plt.plot(res.t, res.y.T) (сюжет был бы более гладким, если бы я предоставил t_eval как уже упоминалось).

plot of solution

наконец, если бы система включала уравнения порядка выше 1, нужно было бы использовать уменьшение до 1-го система заказов.

1