Любые предложения о том, как я могу построить данные типа mixEM с помощью ggplot2

у меня есть образец записей 1m, полученных из моих исходных данных. (Для справки, вы можете использовать эти фиктивные данные, которые могут генерировать приблизительно подобное распределение

b <- data.frame(matrix(rnorm(2000000, mean=c(8,17), sd=2)))
c <- b[sample(nrow(b), 1000000), ]

) Я считал, что гистограмма представляет собой смесь двух логарифмически нормальных распределений, и я попытался подогнать суммированные распределения с помощью алгоритма EM, используя следующий код:

install.packages("mixtools")
lib(mixtools)
#line below returns EM output of type mixEM[] for mixture of normal distributions
c1 <- normalmixEM(c, lambda=NULL, mu=NULL, sigma=NULL) 
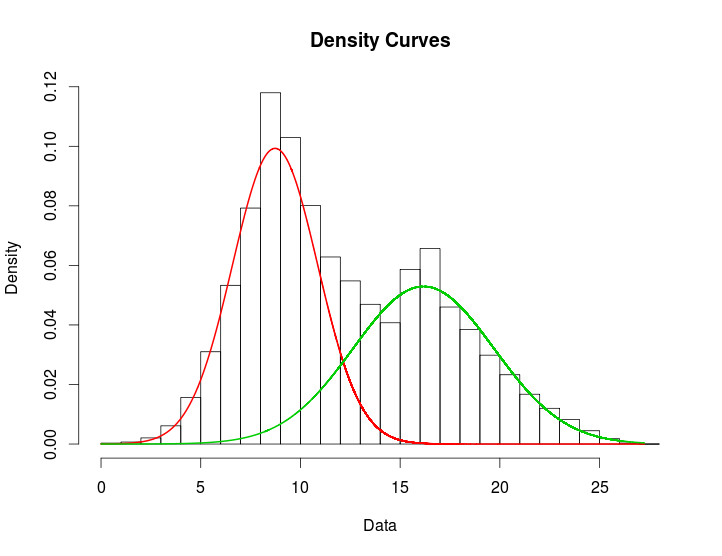
plot(c1, density=TRUE)

первый график-это график логарифмического правдоподобия, а второй (если вы нажмете return снова), дает аналогичное следующие кривые плотности:

Mixture model density curves

Как я уже упоминал, c1 имеет тип mixEM[] , и функция plot () может вместить это. Я хочу заполнить кривые плотности цветами. Это легко сделать с помощью ggplot2 (), но ggplot2 () не поддерживает данные типа mixEM[] и выдает следующее сообщение:

"ggplot не знает, как обращаться с данными класса mixEM" есть ли другой подход, который я могу принять для этой проблемы? Любые предложения значительно ценю!!

спасибо!

6
density-plot em ggplot2 mixture-model r

2 ответов

посмотрите на структуру возвращаемого объекта (это должно быть документировано в справке):

> # simple mixture of normals:
> x=c(rnorm(10000,8,2),rnorm(10000,17,4))
> xMix = normalmixEM(x, lambda=NULL, mu=NULL, sigma=NULL)

что:

> str(xMix)
List of 9
 $ x         : num [1:20000] 6.18 9.92 9.07 8.84 9.93 ...
 $ lambda    : num [1:2] 0.502 0.498
 $ mu        : num [1:2] 7.99 17.05
 $ sigma     : num [1:2] 2.03 4.02
 $ loglik    : num -59877

компоненты lambda, mu и sigma определяют возвращаемые нормальные плотности. Вы можете построить их в ggplot, используя qplot и stat_function. Но Сначала сделайте функцию, которая возвращает масштабированные нормальные плотности:

sdnorm =
function(x, mean=0, sd=1, lambda=1){lambda*dnorm(x, mean=mean, sd=sd)}

затем:

qplot(x,geom="density") + stat_function(fun=sdnorm,arg=list(mean=xMix$mu[1],sd=xMix$sigma[1], lambda=xMix$lambda[1]),fill="blue",geom="polygon")  + stat_function(fun=sdnorm,arg=list(mean=xMix$mu[2],sd=xMix$sigma[2], lambda=xMix$lambda[2]),fill="#FF0000",geom="polygon")

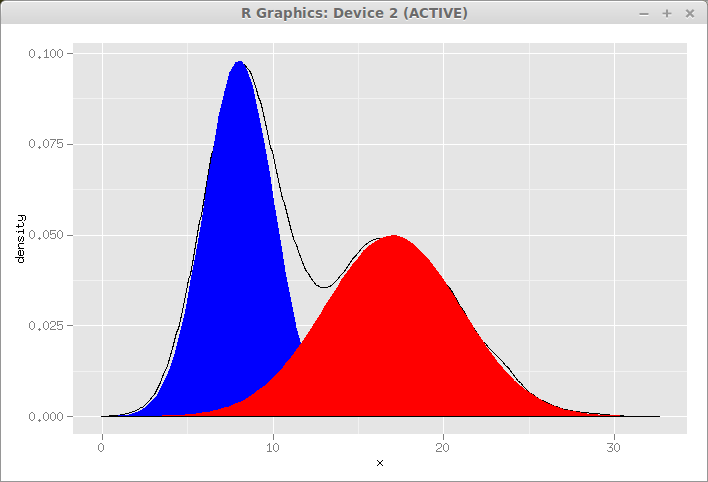
enter image description here

или как там ggplot навыки у вас есть. Прозрачный цвета на плотностях могут быть хороши.

ggplot(data.frame(x=x)) + 
 geom_histogram(aes(x=x,y=..density..),fill="white",color="black") +
 stat_function(fun=sdnorm,
    arg=list(mean=xMix$mu[2],
             sd=xMix$sigma[2],
             lambda=xMix$lambda[2]),
             fill="#FF000080",geom="polygon") +
 stat_function(fun=sdnorm,
    arg=list(mean=xMix$mu[1],
             sd=xMix$sigma[1],
             lambda=xMix$lambda[1]),
             fill="#00FF0080",geom="polygon")

производство:

enter image description here

8

а вот немного другой подход, который использует geom_ploygon(...) вместо нескольких вызовов stat_function(...). Одна проблема с stat_function(...) это вторичные аргументы (mu, sigma и lambda в этом примере), которые передаются с помощью args=list(...) параметр, не может быть включен в эстетическое отображение, поэтому вы должны иметь несколько вызовов stat_function(...) как и решение @Spacedman.

этот подход создает PDF-файлы за пределами ggplot и использует один вызов geom_polygon(...). В результате это работает без модификации для произвольного числа распределений в смеси.

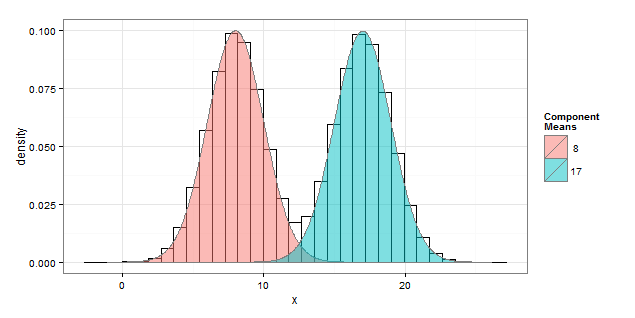
# ggplot mixture plot
gg.mixEM <- function(EM) {
  require(ggplot2)
  x       <- with(EM,seq(min(x),max(x),len=1000))
  pars    <- with(EM,data.frame(comp=colnames(posterior), mu, sigma,lambda))
  em.df   <- data.frame(x=rep(x,each=nrow(pars)),pars)
  em.df$y <- with(em.df,lambda*dnorm(x,mean=mu,sd=sigma))
  ggplot(data.frame(x=EM$x),aes(x,y=..density..)) + 
    geom_histogram(fill=NA,color="black")+
    geom_polygon(data=em.df,aes(x,y,fill=comp),color="grey50", alpha=0.5)+
    scale_fill_discrete("Component\nMeans",labels=format(em.df$mu,digits=3))+
    theme_bw()
}

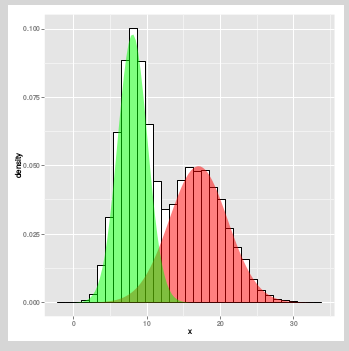
library(mixtools)
# two components
set.seed(1)    # for reproducible example
b <- rnorm(2000000, mean=c(8,17), sd=2)
c <- b[sample(length(b), 1000000) ]
c2 <- normalmixEM(c, lambda=NULL, mu=NULL, sigma=NULL) 
gg.mixEM(c2)


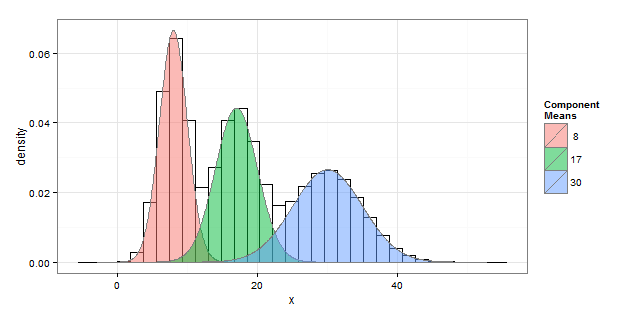
# three components
set.seed(1)
b <- rnorm(2000000, mean=c(8,17,30), sd=c(2,3,5))
c <- b[sample(length(b), 1000000) ]
library(mixtools)
c3 <- normalmixEM(c, k=3, lambda=NULL, mu=NULL, sigma=NULL) 
gg.mixEM(c3)

5