Максимальное число подграфов с заданным минимальным весом
У меня есть неориентированный планарный граф, где каждый узел имеет вес. Я хочу разбить Граф на как можно больше связанных непересекающихся подграфов (EDIT: или достичь минимального среднего веса возможных подграфов), учитывая условие, что каждый подграф должен достичь фиксированного минимального веса (который является суммой весов его узлов). Подграф, содержащий только один узел, также в порядке (если вес узла больше фиксированного минимума).
то, что я узнал, так далеко эвристика:
create a subgraph out of every node
while there is an underweight subgraph:
select the subgraph S with the lowest weight
find a subgraph N that has the lowest weight among the neighbouring subgraphs of S
merge S to N
очевидно, что это не оптимально. У кого-нибудь есть лучшее решение? (Возможно, я просто невежествен, и это не сложная проблема, но я никогда не изучал теорию графов...)
изменить (больше деталей фона): узлы в этом графе являются мелкие административные единицы, для которых статистические данные должны быть предоставлены. Тем не менее, единицы должны иметь определенный минимальный размер населения, чтобы избежать конфликтов с законодательством О персональных данных. Моя цель создавать агрегаты так, чтобы по пути терялось как можно меньше информации. Отношения окрестности служат ребрами графа, так как результирующие единицы должны быть смежными.
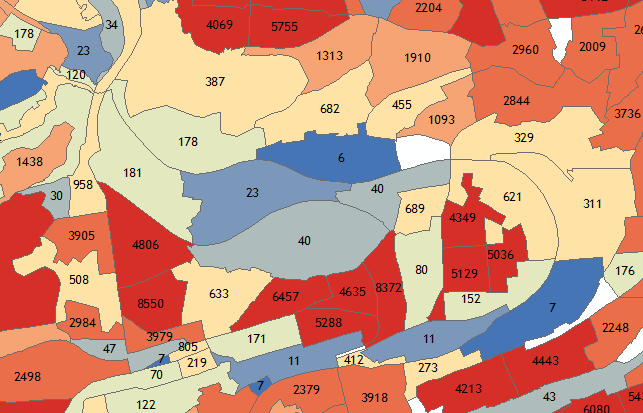
большинство единиц (узлов) в наборе значительно выше минимального порога. Около 5-10 % из них ниже порога с различными размерами, как показано на примере (минимальный размер 50):
3 ответов
Это NP-трудная задача оптимизации. Например,проблема раздела можно легко свести к этому (свойство planarity не вызывает проблем). Таким образом, алгоритм, который вычисляет оптимальное решение (и вы, похоже, просите оптимальное решение в своем комментарии), вряд ли будет практичным для "десятков тысяч узлов".
Если вам на самом деле не нужно оптимальное решение, но хорошее, я бы использовал локальные методы оптимизации, такие как tabu поиска и имитации отжига.
потому что средний вес подгр вес от общего графика, деленная на число подграфов, важно только то, чтобы найти максимальное число подграфов можно достичь. Угадайте это число, N, сформируйте начальное разбиение на N подграфов, а затем, например, используйте локальные перемещения (1) перемещения узла из одного подграфа в другой и (2) обмена двумя узлами между двумя соседними подграфами в поисках приемлемого решение, в котором каждый подграф имеет необходимый минимальный вес. Если вы не можете найти приемлемое решение вообще, уменьшите N (например, на единицу) и перезапустите, пока не найдете решение.
детали экземпляра изменяют все.
называем вершины тяжелый если он сам по себе превышает порог. Никогда не имеет смысла иметь подграф с двумя тяжелыми вершинами, потому что мы можем разделить его на две части. Таким образом, число подграфов в оптимальном решении аддитивно связано с числом подграфов, не содержащих тяжелой вершины.
в результате мы можем удалить тяжелые вершины и сосредоточиться на создании как можно большего количества допустимых подграфов из того что осталось. Судя по вашей карте, то, что осталось, будет состоять из многих связанных компонентов, каждый из которых имеет только несколько вершин. Допустимые подграфы должны быть связаны, поэтому эти компоненты могут быть решены независимо. В небольших экземплярах можно (например) перечислить все допустимые подграфы, а затем запустить Алгоритм X чтобы найти упаковку максимальной мощности.
проблема NP-жесткая, тогда я выделю экспоненциальное решение. Это решение имеет много улучшающих моментов,я выделю некоторые.
вся идея такова: каждый раздел вершины связан некоторыми ребрами, тогда вы можете убедиться, что если вы попытаетесь со всеми возможными наборами ребер, которые делают правильный раздел Графика. Вы можете найти наилучший вариант подсчета количества наборов каждого раздела (оптимальное условие).
в вашем предыдущем подходе вы не есть домен для расширения поиска. Для решения были использованы следующие: - Непересекающиеся наборы: представление разделов - Наборы питания: для поиска всех возможных наборов ребер
public Partition Solve(Graph g, int min)
{
int max = 0;
Partition best;
// Find all the possible partitions for Edges
foreach(var S in PowerSet(g.Edges))
{
// Build the Vertexes partition
var partition = BuildPartition(S);
// Test the min condition foreach component
if (IsInvalid(partition, min))
continue;
// Continue if we already have something better
if (max >= partition.Length)
continue;
// Update
max = partition.Length;
best = partition;
}
return best;
}
public Partition BuildPartition(Graph g, IEnumerable<Edge> edges)
{
// Initially Every Vertex in alone in his partition
var partition = new DisjointSet(g.Vertexes);
foreach (var edge in edges)
{
// If the Vertexes of this edge are already in the same partition DO NOTHING
if (partition.Find(edge.V1) == partition.Find(edge.V2))
continue;
// Join both subsets
partition.Union(edge.V1, edge.V2);
}
return parition;
}
public bool IsInvalid(Partition p, int min)
{
return p.Sets.Any(t => t.Sum(v => v.Weight) < min);
}
вы можете улучшить решение в следующих аспектах: - Добавьте параллелизм к условию PowerSet и IsInvalid - Найти лучший способ создания допустимых наборов ребер - Есть некоторый начальный случай для вершины с большим весом, чем minimun (всегда будет в отдельном подграфе)
порядок алгоритм задается набором мощности. - Power Set: в этом случае для n вершинного графа у вас будет в худшем случае 3n-6 ребер, а затем O(2^N). - Раздел сборки: V + E * LogV тогда O(NLogN) - IsInvalid: O (V)
наконец, решение O (2^N * N * LogN) Используйте эту последнюю формулу для вычисления количества операций
надеюсь, что это поможет!
