Маркировка вершин многоугольника в Mathematica

учитывая набор точек в плоскости T={a1,a2,...,an} затем Graphics[Polygon[T]] построит полигон, созданный точками. Как добавить метки к вершинам многоугольника? Иметь только индекс в качестве метки было бы лучше, чем ничего. Есть идеи?

6
plot wolfram-mathematica

3 ответов

pts = {{1, 0}, {0, Sqrt[3]}, {-1, 0}};
Graphics[
 {{LightGray, Polygon[pts]},
  {pts /. {x_, y_} :> Text[Style[{x, y}, Red], {x, y}]}}
 ]

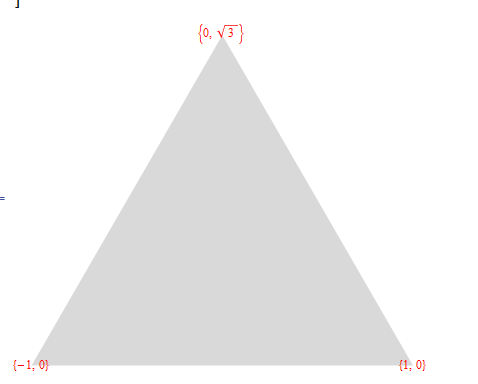
enter image description here

добавить точку и

pts = {{1, 0}, {0, Sqrt[3]}, {-1, 0}};
Graphics[
 {{LightGray, Polygon[pts]},
  {pts /. {x_, y_} :> Text[Style[{x, y}, Red], {x, y}, {0, -1}]},
  {pts /. {x_, y_} :> {Blue, PointSize[0.02], Point[{x, y}]}}
  }
 ]

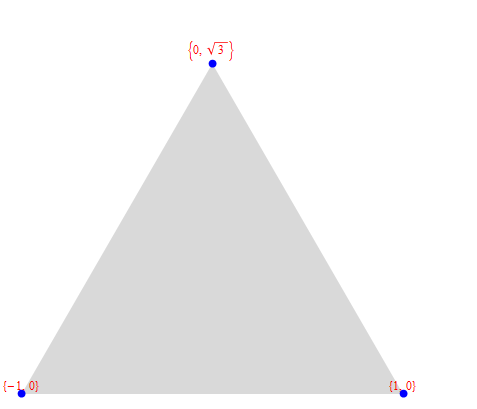
enter image description here

обновление:

использовать индекс:

pts = {{1, 0}, {0, Sqrt[3]}, {-1, 0}};
Graphics[
 {{LightGray, Polygon[pts]},
  {pts /. {x_, y_} :> 
     Text[Style[Position[pts, {x, y}], Red], {x, y}, {0, -1}]}
  }
 ]

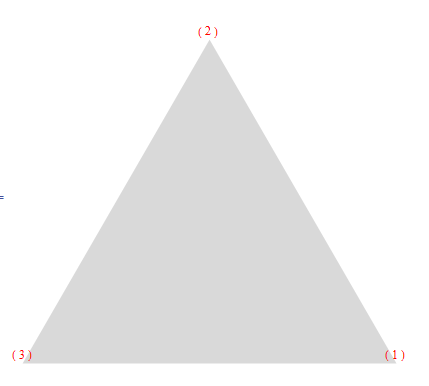
enter image description here

9

версия Насера (обновление) использует шаблоны. Этот использует функциональное программирование. MapIndexed дает вам как координаты, так и их индекс без необходимости Position, чтобы найти его.

pts = {{1, 0}, {0, Sqrt[3]}, {-1, 0}};
Graphics[
 {
  {LightGray, Polygon[pts]},
  MapIndexed[Text[Style[#2[[1]], Red], #1, {0, -1}] &, pts]
  }
 ]

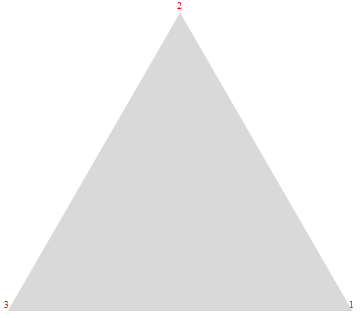
enter image description here

или, если вам не нравится MapIndexed, вот версия с Apply (на уровне 1, инфиксная нотация @@@).

pts = {{1, 0}, {0, Sqrt[3]}, {-1, 0}};
idx = Range[Length[pts]];
Graphics[
 {
  {LightGray, Polygon[pts]},
  Text[Style[#2, Red], #1, {0, -1}] & @@@ ({pts, idx}\[Transpose])
  }
 ]

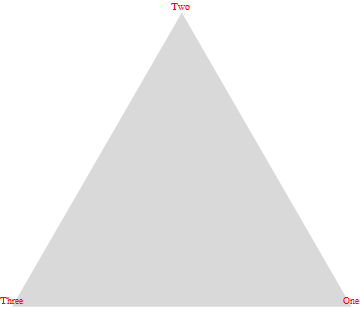
это можно расширить до произвольных меток как следует:

pts = {{1, 0}, {0, Sqrt[3]}, {-1, 0}};
idx = {"One", "Two", "Three"};
Graphics[
 {
  {LightGray, Polygon[pts]},
  Text[Style[#2, Red], #1, {0, -1}] & @@@ ({pts, idx}\[Transpose])
  }
 ]

enter image description here

7

вы можете использовать параметры GraphPlot для этого. Пример:

c = RandomReal[1, {3, 2}]
g = GraphPlot[c, VertexLabeling -> True, VertexCoordinateRules -> c];

Graphics[{Polygon@c, g[[1]]}]

таким образом, вы также можете использовать VertexLabeling -> Tooltip или VertexRenderingFunction если вы хотите. Если вы не хотите, чтобы края накладывались, вы можете добавить EdgeRenderingFunction -> None до

0