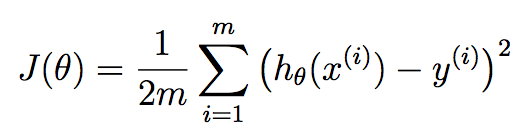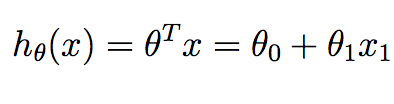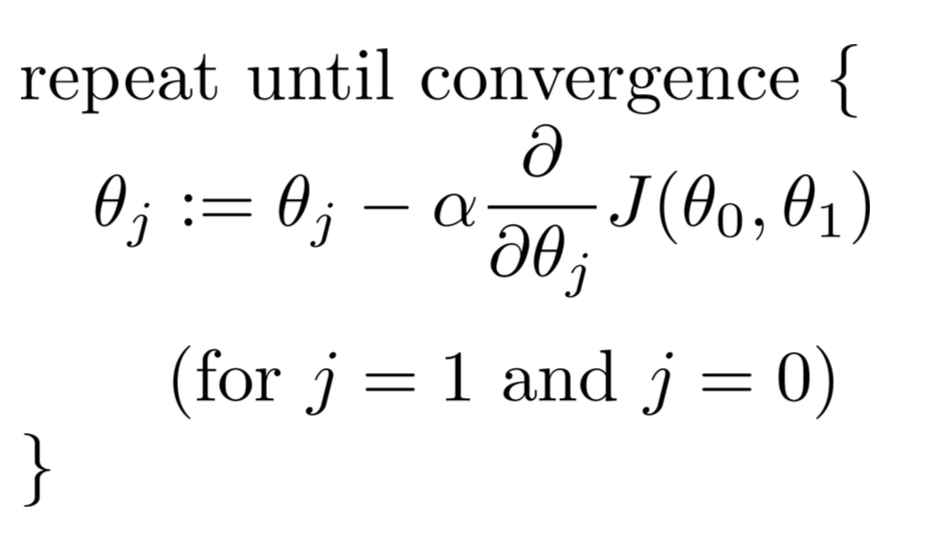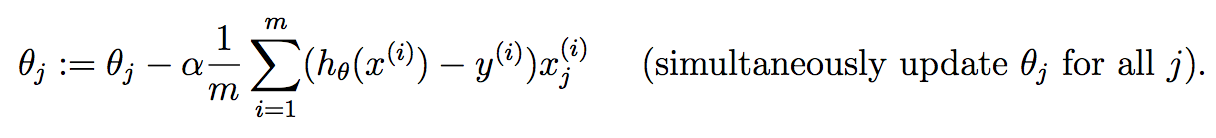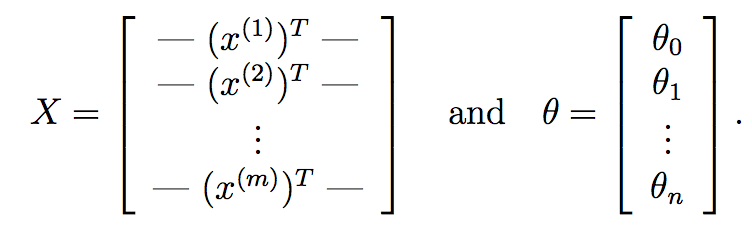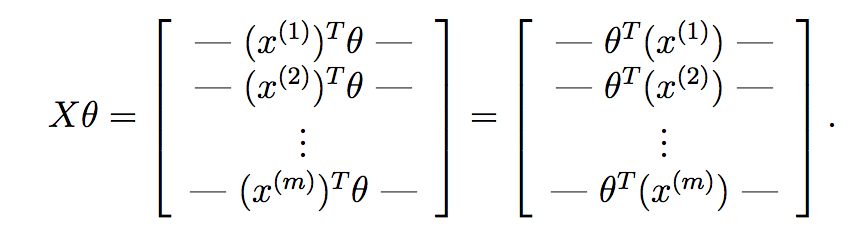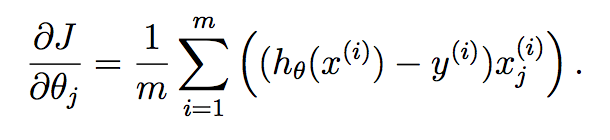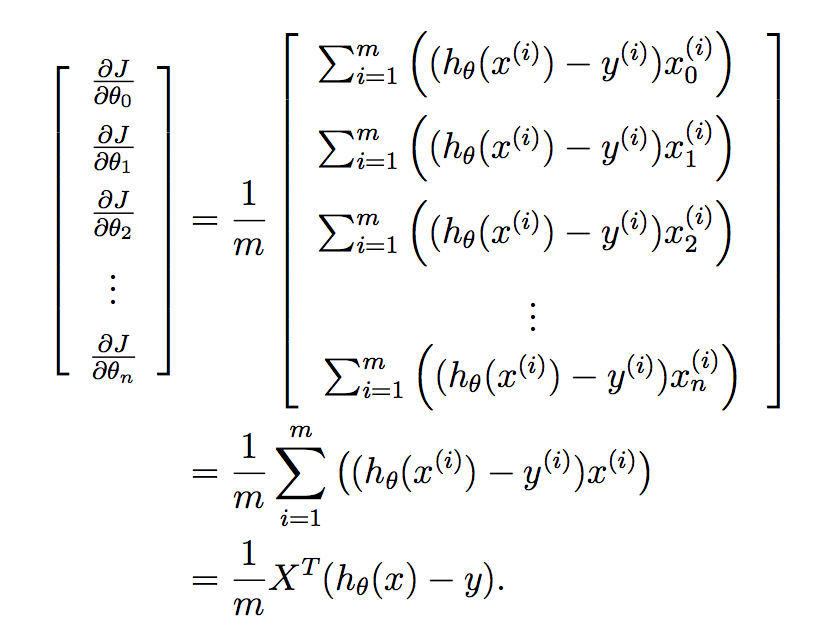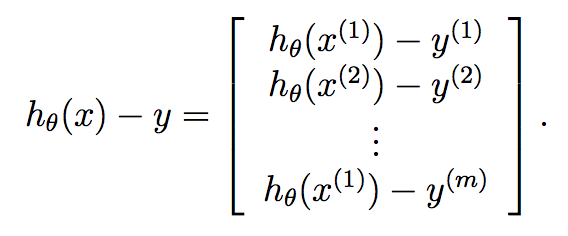ошибка очень проста. Ваш delta объявление должно быть внутри первого for петли. Каждый раз, когда вы накапливаете взвешенные различия между учебной выборкой и выходом, вы должны начать накапливать с самого начала.

не делая этого, то, что вы делаете, накапливает ошибки из предыдущей итерации который принимает ошибку предыдущей изученной версии theta С учетом того, что это неправильно. Вы должны в начале первого for петли.

кроме того, у вас, кажется, есть посторонний computeCost звонок. Я предполагаю, что это вычисляет функцию на каждой итерации с учетом текущих параметров, и так я собираюсь создать новый массив на выходе cost это показывает вам это на каждой итерации. Я также собираюсь вызвать эту функцию и назначить ее соответствующим элементам в этом массиве:

function [theta, costs] = gradientDescent(X, y, theta, alpha, iterations)
    m = length(y);
    costs = zeros(m,1); %// New
%    delta=zeros(2,1); %// Remove
    for iter =1:1:iterations
    delta=zeros(2,1); %// Place here
   for i=1:1:m
       delta(1,1)= delta(1,1)+( X(i,:)*theta - y(i,1))  ;
       delta(2,1)=delta(2,1)+ (( X(i,:)*theta - y(i,1))*X(i,2)) ;
   end
    theta= theta-( delta*(alpha/m) );
   costs(iter) = computeCost(X,y,theta); %// New
end
end

Примечание правильная векторизация

FWIW, я не считаю эту реализацию полностью векторизованной. Вы можете устранить второй for цикл с помощью векторизованных операций. Прежде чем мы это сделаем, позвольте мне изложить некоторую теорию, чтобы мы были на одной странице. Вы используете градиентный спуск здесь в терминах линейной регрессии. Мы хотим искать лучшие параметры theta это наши коэффициенты линейной регрессии, которые стремятся минимизировать эту стоимость функция:

m соответствует количеству учебных образцов, которые мы имеем в наличии и x^{i} соответствует i^th пример подготовки. y^{i} соответствует основному значению истины, которое мы связали с i^th обучающей выборки. h это наша гипотеза, и она определяется как:

обратите внимание, что в контексте линейного регрессия в 2D, у нас есть только два значения в theta мы хотим вычислить-термин перехвата и наклон.

мы можем уменьшить функцию цены J определить лучшие коэффициенты регрессии, которые могут дать нам лучшие прогнозы, которые минимизируют ошибку обучающего набора. В частности, начиная с некоторых начальных theta параметры... обычно вектор нулей, мы перебираем итерации от 1 до столько, сколько считаем нужным, и на каждой итерации мы обновляем наши theta параметры по этой зависимости:

для каждого параметра, который мы хотим обновить, вам нужно определить градиент функции затрат по каждой переменной и оценить, что это такое в текущем состоянии theta. Если вы решите это с помощью исчисления, мы получим:

Если вам неясно, как этот вывод произошел, то я отсылаю вас к этой хорошей математике Сообщение Stack Exchange, которое говорит об этом:

https://math.stackexchange.com/questions/70728/partial-derivative-in-gradient-descent-for-two-variables

сейчас... как мы можем применить это к нашей нынешней проблеме? В частности, вы можете рассчитать записи delta довольно легко анализировать все образцы вместе за один раз. Я имею в виду, что вы можете просто сделать это:

function [theta, costs] = gradientDescent(X, y, theta, alpha, iterations)
    m = length(y);
    costs = zeros(m,1);
    for iter = 1 : iterations
        delta1 = theta(1) - (alpha/m)*(sum((theta(1)*X(:,1) + theta(2)*X(:,2) - y).*X(:,1)));
        delta2 = theta(2) - (alpha/m)*(sum((theta(1)*X(:,1) + theta(2)*X(:,2) - y).*X(:,2)));

        theta = [delta1; delta2];
        costs(iter) = computeCost(X,y,theta);
    end
end

операции delta(1) и delta(2) can полностью векторизоваться в одном операторе для обоих. Что вы делаете theta^{T}*X^{i} для каждого образца i С 1, 2, ..., m. Вы можете удобно разместить это в одном sum заявление.

мы можем пойти еще дальше и заменить это чисто матричными операциями. Во-первых, то, что вы можете сделать, это вычислить theta^{T}*X^{i} для каждого входного образца X^{i} очень быстро используя умножение матрицы. Предположим, если:

здесь, X наша матрица данных, которая состоит из m строк, соответствующих m учебные образцы и n столбцы, соответствующие n функции. Аналогично,theta наш выученный вектор веса от градиентного спуска с n+1 особенности учета срока перехвата.

если вычислить X*theta, мы получим:

как вы можете видеть здесь, мы вычислили гипотезу для каждого образца и имеем поместите каждый в вектор. Каждый элемент этого вектора является гипотезой для i^th обучающей выборки. Теперь вспомните, какой градиентный член каждого параметра находится в градиентном спуске:

мы хотим реализовать это все за один раз для всех параметров в вашем изученном векторе, и поэтому помещение этого в вектор дает мы:

и наконец:

Итак, мы знаем, что y уже является вектором длины m, и поэтому мы можем очень компактно вычислить градиентный спуск на каждой итерации по:

theta = theta - (alpha/m)*X'*(X*theta - y);

.... таким образом, ваш код теперь просто:

function [theta, costs] = gradientDescent(X, y, theta, alpha, iterations)
    m = length(y);
    costs = zeros(m, 1);
    for iter = 1 : iterations
        theta = theta - (alpha/m)*X'*(X*theta - y);
        costs(iter) = computeCost(X,y,theta);
    end
end