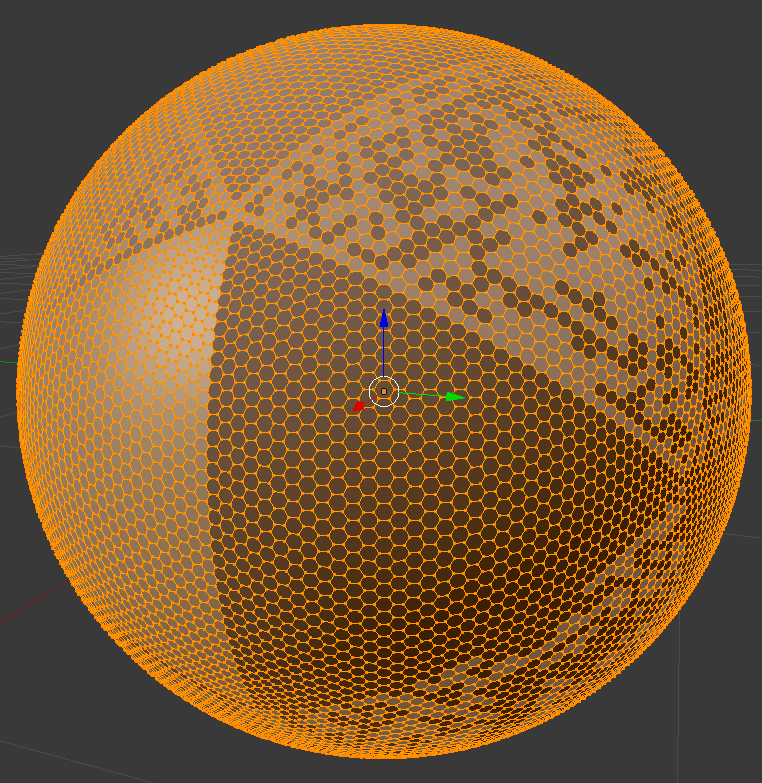
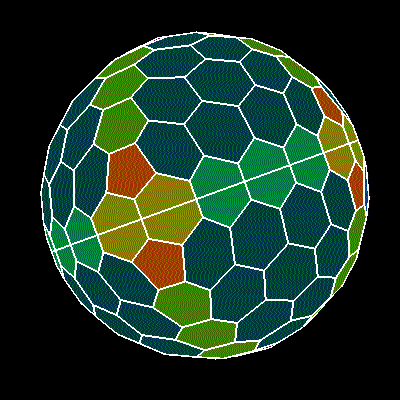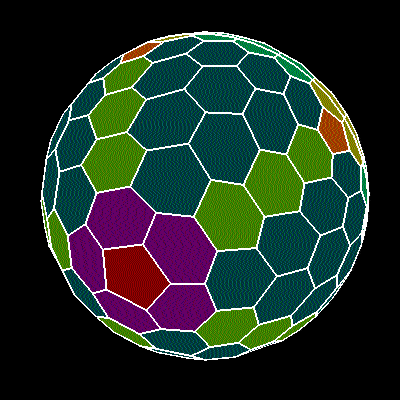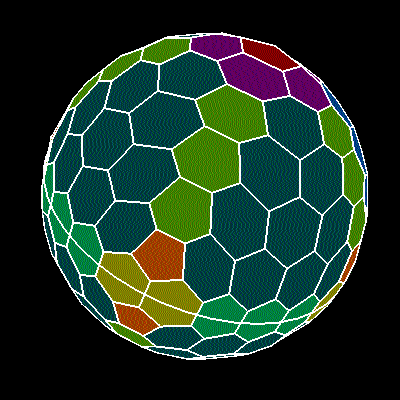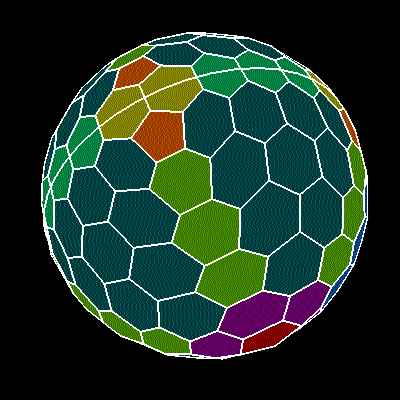
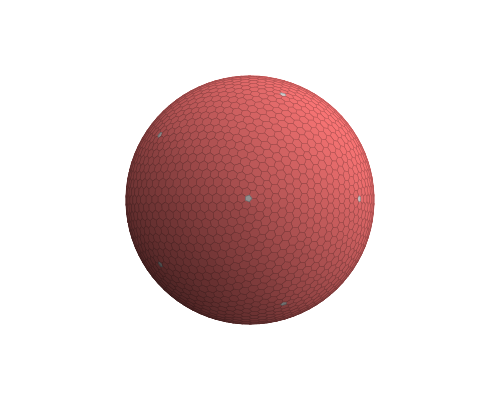
Математически полученная сферическая гексагональная решетка
Я пытаюсь создать форму, подобную этой, шестиугольники с 12 пятиугольниками, произвольного размера.
единственное, я понятия не имею, какой код потребуется для его создания!
цель состоит в том, чтобы иметь возможность взять точку в 3D-пространстве и преобразовать ее в координату положения на сетке или наоборот и занять позицию сетки и получить соответствующую вершины для рисования сетки.
Я даже не знаю, как хранить позиции сетки для этого. Каждый раздел "triagle" между 3 пятиугольников сделать свой собственный набор 2D координаты?
Я, скорее всего, будет на C# для этого, но меня больше интересует, какие алгоритмы использовать для этого и объяснение того, как они будут работать, а не кто-то просто дал мне кусок кода.
3 ответов
сначала некоторый анализ изображения в вопросе: сферический треугольник, охватываемый соседними центрами Пентагона, кажется равносторонним. Когда пять равносторонних треугольников встречаются в одном углу и охватывают всю сферу, это может быть только конфигурации, вызванные икосаэдр. Таким образом, есть 12 пятиугольников и 20 патчей треугольного выреза в hexongal сетки подключенный к сфере.
таким образом, это способ построить такую гексагональную сетку на сфера:
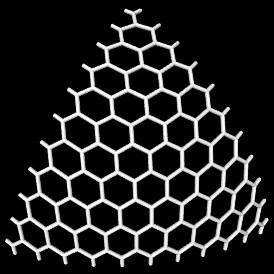
создать треугольный вырез шестиугольной сетки: фиксированный треугольник (я выбрал (-0.5,0),(0.5,0),(0,sqrt (3) / 2)) накладывается гексагональная сетка с желаемым разрешением
ns.т. углы треугольника совпадают с центрами шестиугольника, см. примеры дляn = 0,1,2,20: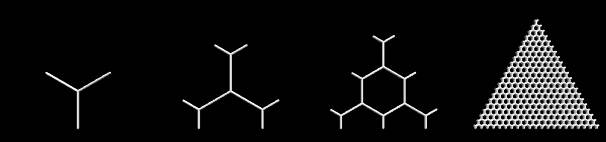
вычислить углы икосаэдр и определите 20 треугольных граней (см. код ниже). Углы икосаэдр определяет центры пятиугольников, грани икосаэдра определяют участки отображенных шестиугольных сеток. (Икосаэдр дает лучшее обычный разделение поверхности сферы на треугольники, т. е. разделение на конгруэнтные равносторонние треугольники. Другие такие деления могут быть получены из тетраэдра или октаэдра; тогда в углах треугольников будут треугольники или квадраты, соответственно. Кроме того, чем меньше и больше треугольников, тем неизбежные искажения при любом отображении плоской сетки на криволинейную поверхность более заметны. Таким образом, выбор икосаэдра в качестве основы для треугольных патчей помогает свести к минимуму искажение шестиугольников.)
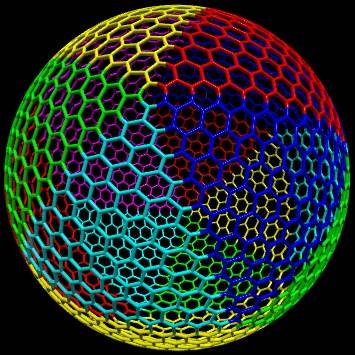
сопоставьте треугольный вырез шестиугольной сетки со сферическими треугольниками, соответствующими граням икоседера: двойной -slerp на основе барицентрическими координатами делает трюк. Ниже приведена иллюстрация отображения треугольного выреза шестиугольной сетки с разрешением
n = 10на один сферический треугольник (определенный одной гранью icosaeder), и иллюстрация отображения сетки на все эти сферические треугольники, охватывающие всю сферу (разные цвета для разных отображений):
вот код Python для генерации углов (координат) и треугольников (точечных индексов) икосаэдр:
from math import sin,cos,acos,sqrt,pi
s,c = 2/sqrt(5),1/sqrt(5)
topPoints = [(0,0,1)] + [(s*cos(i*2*pi/5.), s*sin(i*2*pi/5.), c) for i in range(5)]
bottomPoints = [(-x,y,-z) for (x,y,z) in topPoints]
icoPoints = topPoints + bottomPoints
icoTriangs = [(0,i+1,(i+1)%5+1) for i in range(5)] +\
[(6,i+7,(i+1)%5+7) for i in range(5)] +\
[(i+1,(i+1)%5+1,(7-i)%5+7) for i in range(5)] +\
[(i+1,(7-i)%5+7,(8-i)%5+7) for i in range(5)]
и вот код Python для сопоставления (точек) фиксированного треугольника со сферическим треугольником с помощью двойного slerp:
# barycentric coords for triangle (-0.5,0),(0.5,0),(0,sqrt(3)/2)
def barycentricCoords(p):
x,y = p
# l3*sqrt(3)/2 = y
l3 = y*2./sqrt(3.)
# l1 + l2 + l3 = 1
# 0.5*(l2 - l1) = x
l2 = x + 0.5*(1 - l3)
l1 = 1 - l2 - l3
return l1,l2,l3
from math import atan2
def scalProd(p1,p2):
return sum([p1[i]*p2[i] for i in range(len(p1))])
# uniform interpolation of arc defined by p0, p1 (around origin)
# t=0 -> p0, t=1 -> p1
def slerp(p0,p1,t):
assert abs(scalProd(p0,p0) - scalProd(p1,p1)) < 1e-7
ang0Cos = scalProd(p0,p1)/scalProd(p0,p0)
ang0Sin = sqrt(1 - ang0Cos*ang0Cos)
ang0 = atan2(ang0Sin,ang0Cos)
l0 = sin((1-t)*ang0)
l1 = sin(t *ang0)
return tuple([(l0*p0[i] + l1*p1[i])/ang0Sin for i in range(len(p0))])
# map 2D point p to spherical triangle s1,s2,s3 (3D vectors of equal length)
def mapGridpoint2Sphere(p,s1,s2,s3):
l1,l2,l3 = barycentricCoords(p)
if abs(l3-1) < 1e-10: return s3
l2s = l2/(l1+l2)
p12 = slerp(s1,s2,l2s)
return slerp(p12,s3,l3)
[полное повторное редактирование 18.10.2017]
хранение геометрии на вас. Либо вы храните его в какой-то сетке, либо генерируете его на лету. Я предпочитаю хранить его. В виде 2 таблиц. Один держит все вершины (без дубликатов), а другой держит 6 индексов используемых точек на каждый шестнадцатеричный вы получили и некоторую дополнительную информацию, такую как сферическое положение, чтобы облегчить пост-обработку.
теперь как генерировать это:
-
создать шестигранной треугольник
размер должен быть радиус сферы. не включайте угловую шестнадцатеричность, а также пропустите последнюю линию треугольника (как радиальную, так и осевую, поэтому между соседними треугольниками на сфере есть 1 шестнадцатеричный зазор), так как это будет перекрываться при объединении сегментов треугольника.
-
преобразование
60degшестигранник треугольник72degпирогтак просто перевести единицы: полярные кордианты (
radius,angle), треугольник вокруг0 deg. Тогда умножьте радиус наcos(angle)/cos(30);, который преобразует треугольник в пирог. А затем масштабировать угол с соотношением72/60. Это сделает наш треугольник объединяемым... -
копировать и вращать треугольник, чтобы заполнить 5 сегментов Пентагона
легко просто поверните точки первого треугольника и сохраните как новый.
-
вычислить
zна основе этого шестиугольная обработка полусферы вы можете конвертировать расстояние в 2Д карта в длину дуги, чтобы ограничить искажения, насколько это возможно.
однако, когда я попробовал (пример ниже), шестиугольники немного искажены, поэтому глубина и масштабирование требуют некоторой настройки. Или после обработки последнего.
-
скопировать половину сферы, чтобы сформировать сфера
просто скопируйте точки / hexes и отрицайте
zось (или поворот на 180 градусов, если вы хотите сохранить обмотку). -
добавить экватор и все недостающие пятиугольники и гексы
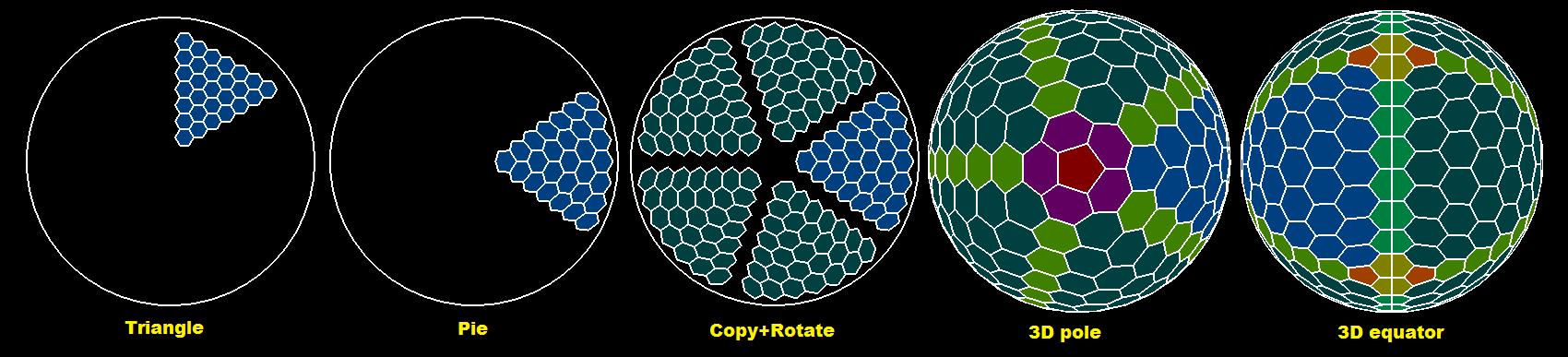
вы должны использовать координаты соседних гексов, чтобы в сетку не добавлялось больше искажений и перекрытий. Здесь предварительный просмотр:
синий is начальный треугольник. темный синий его копии. Красный пятиугольники полюса. темно-зеленый - это экватор, светло-зеленый являются линиями соединения между треугольниками. В желтовато недостающие экватор шестиугольники рядом Темно-Оранжевый пятиугольников.
//$$---- Form CPP ----
//---------------------------------------------------------------------------
#include <vcl.h>
#include <math.h>
#pragma hdrstop
#include "win_main.h"
#include "gl/OpenGL3D_double.cpp"
#include "PolyLine.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TMain *Main;
OpenGLscreen scr;
bool _redraw=true;
double animx= 0.0,danimx=0.0;
double animy= 0.0,danimy=0.0;
//---------------------------------------------------------------------------
PointTab pnt; // (x,y,z)
struct _hexagon
{
int ix[6]; // index of 6 points, last point duplicate for pentagon
int a,b; // spherical coordinate
DWORD col; // color
// inline
_hexagon() {}
_hexagon(_hexagon& a) { *this=a; }
~_hexagon() {}
_hexagon* operator = (const _hexagon *a) { *this=*a; return this; }
//_hexagon* operator = (const _hexagon &a) { ...copy... return this; }
};
List<_hexagon> hex;
//---------------------------------------------------------------------------
// https://stackoverflow.com/a/46787885/2521214
//---------------------------------------------------------------------------
void hex_sphere(int N,double R)
{
const double c=cos(60.0*deg);
const double s=sin(60.0*deg);
const double sy= R/(N+N-2);
const double sz=sy/s;
const double sx=sz*c;
const double sz2=0.5*sz;
const int na=5*(N-2);
const int nb= N;
const int b0= N;
double *q,p[3],ang,len,l,l0,ll;
int i,j,n,a,b,ix;
_hexagon h,*ph;
hex.allocate(na*nb);
hex.num=0;
pnt.reset3D(N*N);
b=0; a=0; ix=0;
// generate triangle hex grid
h.col=0x00804000;
for (b=1;b<N-1;b++) // skip first line b=0
for (a=1;a<b;a++) // skip first and last line
{
p[0]=double(a )*(sx+sz);
p[1]=double(b-(a>>1))*(sy*2.0);
p[2]=0.0;
if (int(a&1)!=0) p[1]-=sy;
ix=pnt.add(p[0]+sz2+sx,p[1] ,p[2]); h.ix[0]=ix; // 2 1
ix=pnt.add(p[0]+sz2 ,p[1]+sy,p[2]); h.ix[1]=ix; // 3 0
ix=pnt.add(p[0]-sz2 ,p[1]+sy,p[2]); h.ix[2]=ix; // 4 5
ix=pnt.add(p[0]-sz2-sx,p[1] ,p[2]); h.ix[3]=ix;
ix=pnt.add(p[0]-sz2 ,p[1]-sy,p[2]); h.ix[4]=ix;
ix=pnt.add(p[0]+sz2 ,p[1]-sy,p[2]); h.ix[5]=ix;
h.a=a;
h.b=N-1-b;
hex.add(h);
} n=hex.num; // remember number of hexs for the first triangle
// distort points to match area
for (ix=0;ix<pnt.nn;ix+=3)
{
// point pointer
q=pnt.pnt.dat+ix;
// convert to polar coordinates
ang=atan2(q[1],q[0]);
len=vector_len(q);
// match area of pentagon (72deg) triangle as we got hexagon (60deg) triangle
ang-=60.0*deg; // rotate so center of generated triangle is angle 0deg
while (ang>+60.0*deg) ang-=pi2;
while (ang<-60.0*deg) ang+=pi2;
len*=cos(ang)/cos(30.0*deg); // scale radius so triangle converts to pie
ang*=72.0/60.0; // scale up angle so rotated triangles merge
// convert back to cartesian
q[0]=len*cos(ang);
q[1]=len*sin(ang);
}
// copy and rotate the triangle to cover pentagon
h.col=0x00404000;
for (ang=72.0*deg,a=1;a<5;a++,ang+=72.0*deg)
for (ph=hex.dat,i=0;i<n;i++,ph++)
{
for (j=0;j<6;j++)
{
vector_copy(p,pnt.pnt.dat+ph->ix[j]);
rotate2d(-ang,p[0],p[1]);
h.ix[j]=pnt.add(p[0],p[1],p[2]);
}
h.a=ph->a+(a*(N-2));
h.b=ph->b;
hex.add(h);
}
// compute z
for (q=pnt.pnt.dat,ix=0;ix<pnt.nn;ix+=pnt.dn,q+=pnt.dn)
{
q[2]=0.0;
ang=vector_len(q)*0.5*pi/R;
q[2]=R*cos(ang);
ll=fabs(R*sin(ang)/sqrt((q[0]*q[0])+(q[1]*q[1])));
q[0]*=ll;
q[1]*=ll;
}
// copy and mirror the other half-sphere
n=hex.num;
for (ph=hex.dat,i=0;i<n;i++,ph++)
{
for (j=0;j<6;j++)
{
vector_copy(p,pnt.pnt.dat+ph->ix[j]);
p[2]=-p[2];
h.ix[j]=pnt.add(p[0],p[1],p[2]);
}
h.a= ph->a;
h.b=-ph->b;
hex.add(h);
}
// create index search table
int i0,i1,j0,j1,a0,a1,ii[5];
int **ab=new int*[na];
for (a=0;a<na;a++)
{
ab[a]=new int[nb+nb+1];
for (b=-nb;b<=nb;b++) ab[a][b0+b]=-1;
}
n=hex.num;
for (ph=hex.dat,i=0;i<n;i++,ph++) ab[ph->a][b0+ph->b]=i;
// add join ring
h.col=0x00408000;
for (a=0;a<na;a++)
{
h.a=a;
h.b=0;
a0=a;
a1=a+1; if (a1>=na) a1-=na;
i0=ab[a0][b0+1];
i1=ab[a1][b0+1];
j0=ab[a0][b0-1];
j1=ab[a1][b0-1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i1].ix[1];
h.ix[1]=hex[i0].ix[0];
h.ix[2]=hex[i0].ix[1];
h.ix[3]=hex[j0].ix[1];
h.ix[4]=hex[j0].ix[0];
h.ix[5]=hex[j1].ix[1];
hex.add(h);
ab[h.a][b0+h.b]=hex.num-1;
}
}
// add 2x5 join lines
h.col=0x00008040;
for (a=0;a<na;a+=N-2)
for (b=1;b<N-3;b++)
{
// +b hemisphere
h.a= a;
h.b=+b;
a0=a-b; if (a0< 0) a0+=na; i0=ab[a0][b0+b+0];
a0--; if (a0< 0) a0+=na; i1=ab[a0][b0+b+1];
a1=a+1; if (a1>=na) a1-=na; j0=ab[a1][b0+b+0];
j1=ab[a1][b0+b+1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i0].ix[5];
h.ix[1]=hex[i0].ix[4];
h.ix[2]=hex[i1].ix[5];
h.ix[3]=hex[j1].ix[3];
h.ix[4]=hex[j0].ix[4];
h.ix[5]=hex[j0].ix[3];
hex.add(h);
}
// -b hemisphere
h.a= a;
h.b=-b;
a0=a-b; if (a0< 0) a0+=na; i0=ab[a0][b0-b+0];
a0--; if (a0< 0) a0+=na; i1=ab[a0][b0-b-1];
a1=a+1; if (a1>=na) a1-=na; j0=ab[a1][b0-b+0];
j1=ab[a1][b0-b-1];
if ((i0>=0)&&(i1>=0))
if ((j0>=0)&&(j1>=0))
{
h.ix[0]=hex[i0].ix[5];
h.ix[1]=hex[i0].ix[4];
h.ix[2]=hex[i1].ix[5];
h.ix[3]=hex[j1].ix[3];
h.ix[4]=hex[j0].ix[4];
h.ix[5]=hex[j0].ix[3];
hex.add(h);
}
}
// add pentagons at poles
_hexagon h0,h1;
h0.col=0x00000080;
h0.a=0; h0.b=N-1; h1=h0; h1.b=-h1.b;
p[2]=sqrt((R*R)-(sz*sz));
for (ang=0.0,a=0;a<5;a++,ang+=72.0*deg)
{
p[0]=2.0*sz*cos(ang);
p[1]=2.0*sz*sin(ang);
h0.ix[a]=pnt.add(p[0],p[1],+p[2]);
h1.ix[a]=pnt.add(p[0],p[1],-p[2]);
}
h0.ix[5]=h0.ix[4]; hex.add(h0);
h1.ix[5]=h1.ix[4]; hex.add(h1);
// add 5 missing hexagons at poles
h.col=0x00600060;
for (ph=&h0,b=N-3,h.b=N-2,i=0;i<2;i++,b=-b,ph=&h1,h.b=-h.b)
{
a = 1; if (a>=na) a-=na; ii[0]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[1]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[2]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[3]=ab[a][b0+b];
a+=N-2; if (a>=na) a-=na; ii[4]=ab[a][b0+b];
for (j=0;j<5;j++)
{
h.a=((4+j)%5)*(N-2)+1;
h.ix[0]=ph->ix[ (5-j)%5 ];
h.ix[1]=ph->ix[ (6-j)%5 ];
h.ix[2]=hex[ii[(j+4)%5]].ix[4];
h.ix[3]=hex[ii[(j+4)%5]].ix[5];
h.ix[4]=hex[ii[ j ]].ix[3];
h.ix[5]=hex[ii[ j ]].ix[4];
hex.add(h);
}
}
// add 2*5 pentagons and 2*5 missing hexagons at equator
h0.a=0; h0.b=N-1; h1=h0; h1.b=-h1.b;
for (ang=36.0*deg,a=0;a<na;a+=N-2,ang-=72.0*deg)
{
p[0]=R*cos(ang);
p[1]=R*sin(ang);
p[2]=sz;
i0=pnt.add(p[0],p[1],+p[2]);
i1=pnt.add(p[0],p[1],-p[2]);
a0=a-1;if (a0< 0) a0+=na;
a1=a+1;if (a1>=na) a1-=na;
ii[0]=ab[a0][b0-1]; ii[2]=ab[a1][b0-1];
ii[1]=ab[a0][b0+1]; ii[3]=ab[a1][b0+1];
// hexagons
h.col=0x00008080;
h.a=a; h.b=0;
h.ix[0]=hex[ii[0]].ix[0];
h.ix[1]=hex[ii[0]].ix[1];
h.ix[2]=hex[ii[1]].ix[1];
h.ix[3]=hex[ii[1]].ix[0];
h.ix[4]=i0;
h.ix[5]=i1;
hex.add(h);
h.a=a; h.b=0;
h.ix[0]=hex[ii[2]].ix[2];
h.ix[1]=hex[ii[2]].ix[1];
h.ix[2]=hex[ii[3]].ix[1];
h.ix[3]=hex[ii[3]].ix[2];
h.ix[4]=i0;
h.ix[5]=i1;
hex.add(h);
// pentagons
h.col=0x000040A0;
h.a=a; h.b=0;
h.ix[0]=hex[ii[0]].ix[0];
h.ix[1]=hex[ii[0]].ix[5];
h.ix[2]=hex[ii[2]].ix[3];
h.ix[3]=hex[ii[2]].ix[2];
h.ix[4]=i1;
h.ix[5]=i1;
hex.add(h);
h.a=a; h.b=0;
h.ix[0]=hex[ii[1]].ix[0];
h.ix[1]=hex[ii[1]].ix[5];
h.ix[2]=hex[ii[3]].ix[3];
h.ix[3]=hex[ii[3]].ix[2];
h.ix[4]=i0;
h.ix[5]=i0;
hex.add(h);
}
// release index search table
for (a=0;a<na;a++) delete[] ab[a];
delete[] ab;
}
//---------------------------------------------------------------------------
void hex_draw(GLuint style) // draw hex
{
int i,j;
_hexagon *h;
for (h=hex.dat,i=0;i<hex.num;i++,h++)
{
if (style==GL_POLYGON) glColor4ubv((BYTE*)&h->col);
glBegin(style);
for (j=0;j<6;j++) glVertex3dv(pnt.pnt.dat+h->ix[j]);
glEnd();
}
if (0)
if (style==GL_POLYGON)
{
scr.text_init_pixel(0.1,-0.2);
glColor3f(1.0,1.0,1.0);
for (h=hex.dat,i=0;i<hex.num;i++,h++)
if (abs(h->b)<2)
{
double p[3];
vector_ld(p,0.0,0.0,0.0);
for (j=0;j<6;j++)
vector_add(p,p,pnt.pnt.dat+h->ix[j]);
vector_mul(p,p,1.0/6.0);
scr.text(p[0],p[1],p[2],AnsiString().sprintf("%i,%i",h->a,h->b));
}
scr.text_exit_pixel();
}
}
//---------------------------------------------------------------------------
void TMain::draw()
{
scr.cls();
int x,y;
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0,0.0,-5.0);
glRotated(animx,1.0,0.0,0.0);
glRotated(animy,0.0,1.0,0.0);
hex_draw(GL_POLYGON);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0,0.0,-5.0+0.01);
glRotated(animx,1.0,0.0,0.0);
glRotated(animy,0.0,1.0,0.0);
glColor3f(1.0,1.0,1.0);
glLineWidth(2);
hex_draw(GL_LINE_LOOP);
glCirclexy(0.0,0.0,0.0,1.5);
glLineWidth(1);
scr.exe();
scr.rfs();
}
//---------------------------------------------------------------------------
__fastcall TMain::TMain(TComponent* Owner) : TForm(Owner)
{
scr.init(this);
hex_sphere(10,1.5);
_redraw=true;
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormDestroy(TObject *Sender)
{
scr.exit();
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormPaint(TObject *Sender)
{
_redraw=true;
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormResize(TObject *Sender)
{
scr.resize();
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60,float(scr.xs)/float(scr.ys),0.1,100.0);
_redraw=true;
}
//-----------------------------------------------------------------------
void __fastcall TMain::Timer1Timer(TObject *Sender)
{
animx+=danimx; if (animx>=360.0) animx-=360.0; _redraw=true;
animy+=danimy; if (animy>=360.0) animy-=360.0; _redraw=true;
if (_redraw) { draw(); _redraw=false; }
}
//---------------------------------------------------------------------------
void __fastcall TMain::FormKeyDown(TObject *Sender, WORD &Key, TShiftState Shift)
{
Caption=Key;
if (Key==40){ animx+=2.0; _redraw=true; }
if (Key==38){ animx-=2.0; _redraw=true; }
if (Key==39){ animy+=2.0; _redraw=true; }
if (Key==37){ animy-=2.0; _redraw=true; }
}
//---------------------------------------------------------------------------
я знаю, что это немного беспорядок индекса, а также правило намотки не гарантируется, поскольку я был слишком ленив, чтобы сделать равномерную индексацию. Остерегайтесь a индексы каждого шестнадцатеричного не являются линейными, и если вы хотите использовать их для отображения в 2Д карта вам нужно будет пересчитать его с помощью atan2 on x,y ее центральное положение.
здесь Превью:
все еще присутствуют некоторые искажения. Они вызваны тем, что мы используем 5 треугольников для соединения на экваторе (поэтому соединение гарантировано). Это означает, что окружность 5*R вместо 6.28*R. Как это может быть улучшено с помощью моделирования поля. Просто взять все точки и добавить сократительной силы на основе их расстояние и привязано к сфере поверхности. Запустите симуляцию, и когда колебания ниже порога, вы получите свою сферу сетка...
другим вариантом было бы найти некоторое уравнение для переназначения точек сетки (аналогично тому, что я сделал для преобразования треугольника в круг), которое имело бы лучшие результаты.
форма, которую вы имеете, является одним из так называемых "многогранников Гольдберга", также является геодезические многогранников.
The (довольно элегантных) алгоритм для генерации этого (и многих других) может быть лаконично закодирован в чем-то, что называется Многогранная Нотация Конвея.
строительство легко следовать шаг за шагом, вы можете нажать на изображение ниже, чтобы получить live предварительный просмотр.
многогранник, который вы ищете, может быть сгенерирован из изосаэдра - инициализировать сетку с изосаэдром.

мы применяем "усечение" операция (обозначение Конвея
t) к сетке (sperical отображение этого является футболом).
применить "двойной" оператор (обозначения Конвея
d).
мы снова применяем операцию "усечение". На данный момент рецепт
tdtI(читать справа!). Вы уже видите, к чему все идет.
применяйте шаги 3 и 4 несколько раз, пока вы не будете удовлетворены.
например, ниже приведена сетка для dtdtdtdtI.
Это довольно легко реализовать. Я бы предложил использование структуры данных, которая позволяет легко пересекать окрестности, дает вершину, ребро и т. д. такие как крылатые края или полу-края datastructures для вашей сетки. Вам нужно только реализовать усеченные и двойные операторы для формы, которую вы ищете.