Matlab/ CUDA: моделирование океанских волн
Я изучал "Имитация Океанской Воды" статья исполнителя Jerry Tessendorf и постарались, чтобы программа статистической волновой модели, но я не получить правильный результат и я не понимаю, почему.
в моей программе я пытался только создать поле высоты волны во время t = 0 без каких-либо дальнейших изменений во времени. После выполнения моей программы я получил не то, что ожидал: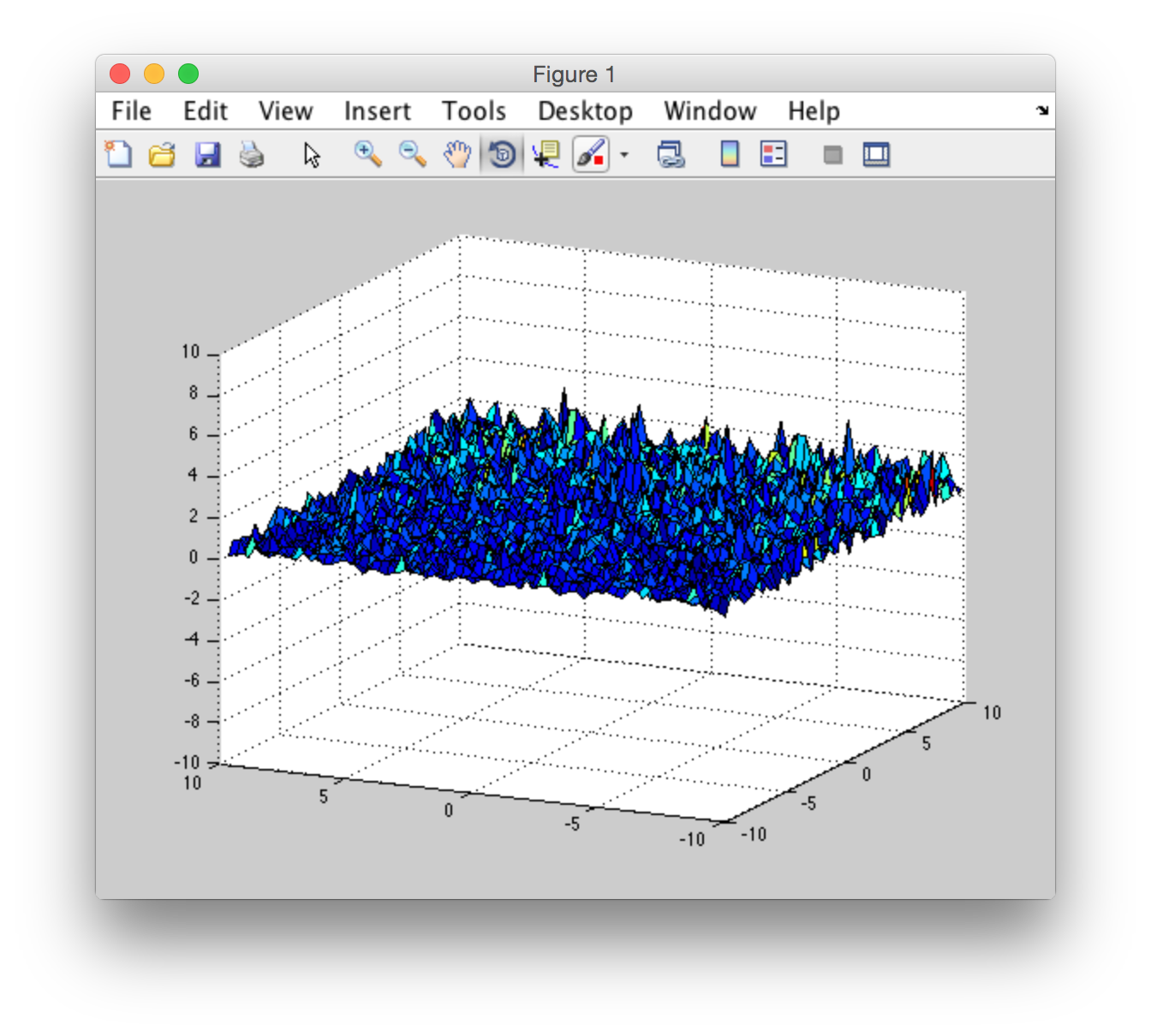
вот мой исходный код:
clear all; close all; clc;
rng(11); % setting seed for random numbers
meshSize = 64; % field size
windDir = [1, 0]; % ||windDir|| = 1
patchSize = 64;
A = 1e+4;
g = 9.81; % gravitational constant
windSpeed = 1e+2;
x1 = linspace(-10, 10, meshSize+1); x = x1(1:meshSize);
y1 = linspace(-10, 10, meshSize+1); y = y1(1:meshSize);
[X,Y] = meshgrid(x, y);
H0 = zeros(size(X)); % height field at time t = 0
for i = 1:meshSize
for j = 1:meshSize
kx = 2.0 * pi / patchSize * (-meshSize / 2.0 + x(i)); % = 2*pi*n / Lx
ky = 2.0 * pi / patchSize * (-meshSize / 2.0 + y(j)); % = 2*pi*m / Ly
P = phillips(kx, ky, windDir, windSpeed, A, g); % phillips spectrum
H0(i,j) = 1/sqrt(2) * (randn(1) + 1i * randn(1)) * sqrt(P);
end
end
H0 = H0 + conj(H0);
surf(X,Y,abs(ifft(H0)));
axis([-10 10 -10 10 -10 10]);
и phillips функция:
function P = phillips(kx, ky, windDir, windSpeed, A, g)
k_sq = kx^2 + ky^2;
L = windSpeed^2 / g;
k = [kx, ky] / sqrt(k_sq);
wk = k(1) * windDir(1) + k(2) * windDir(2);
P = A / k_sq^2 * exp(-1.0 / (k_sq * L^2)) * wk^2;
end
есть ли исходный код моделирования океана matlab, который может помочь мне понять мои ошибки? Быстрый поиск google не дал никаких результатов.
вот "правильный" результат, который я получил от "CUDA FFT Ocean Simulation". Я еще не достиг этого поведения в Matlab, но я загрузил " surf "в matlab, используя данные из"CUDA FFT Ocean Simulation". Вот как это выглядит:
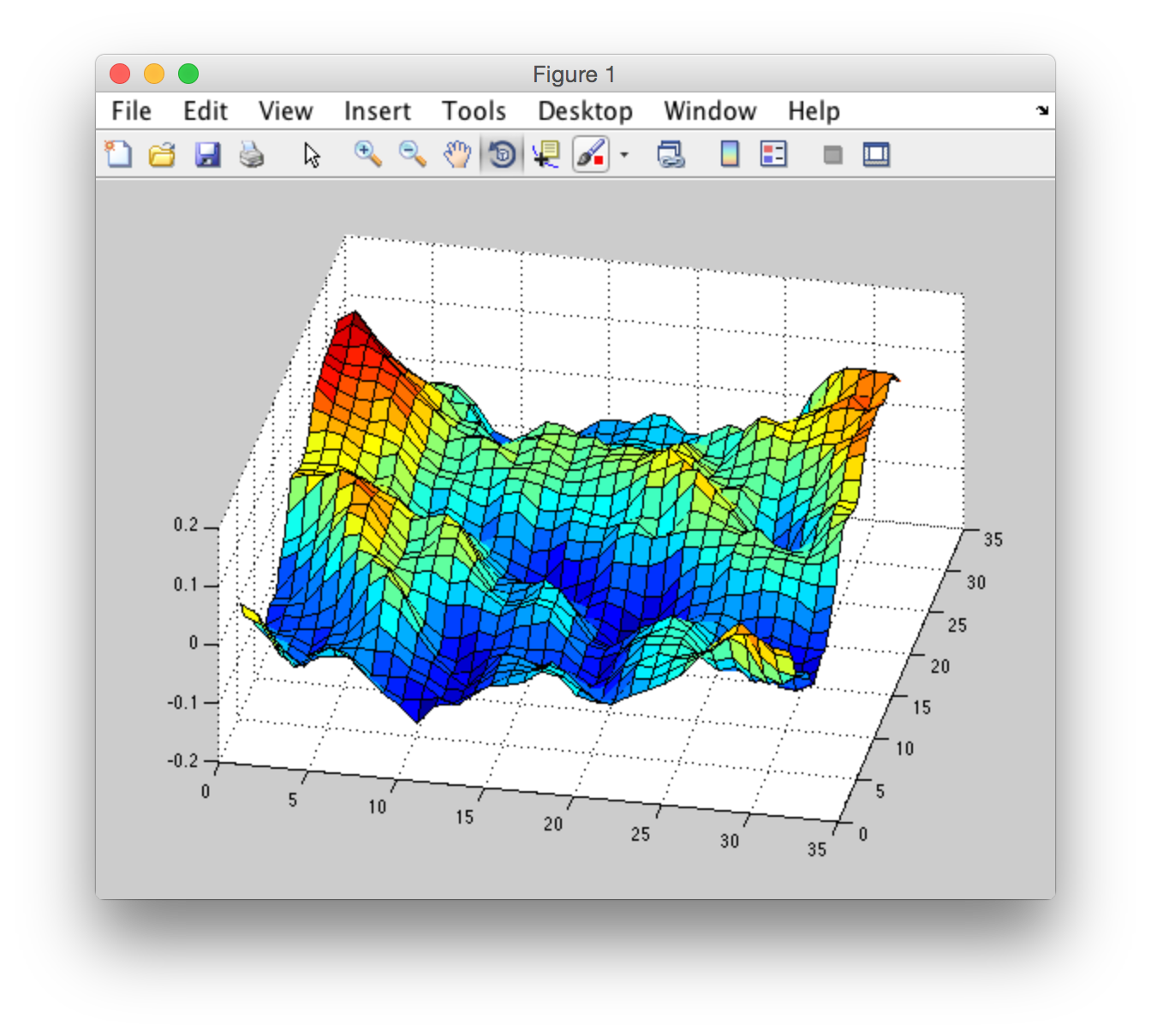
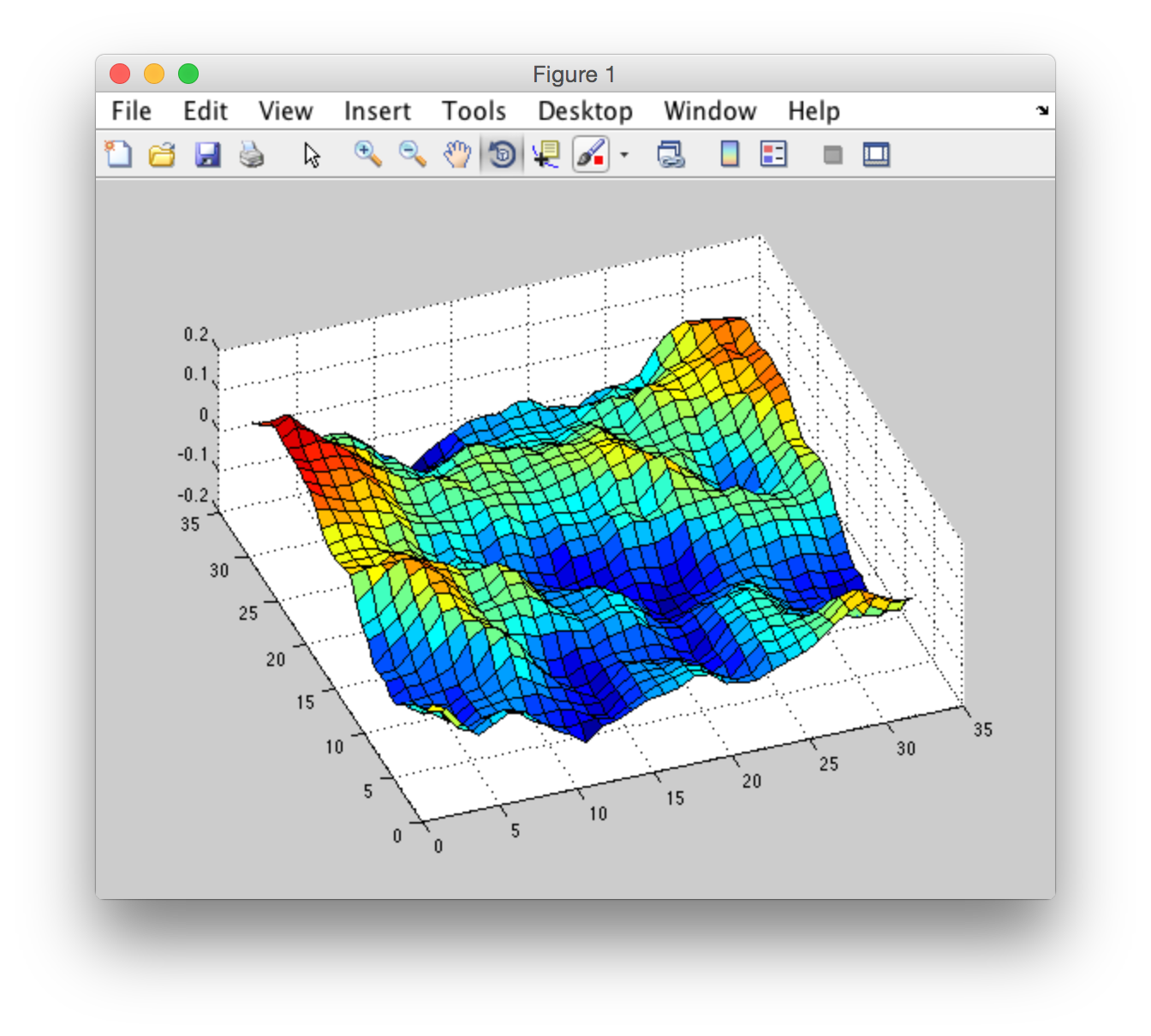
я провел эксперимент и получил интересный результат:
я взял созданный h0 из "CUDA FFT Ocean Simulation". Поэтому я должен сделать ifft для преобразования из частотной области в пространственную область для построения графика. Я сделал это для того же h0 использование matlab ifft и с помощью cufftExecC2C из библиотеки CUDA. Вот результат:
CUDA и ОБПФ:
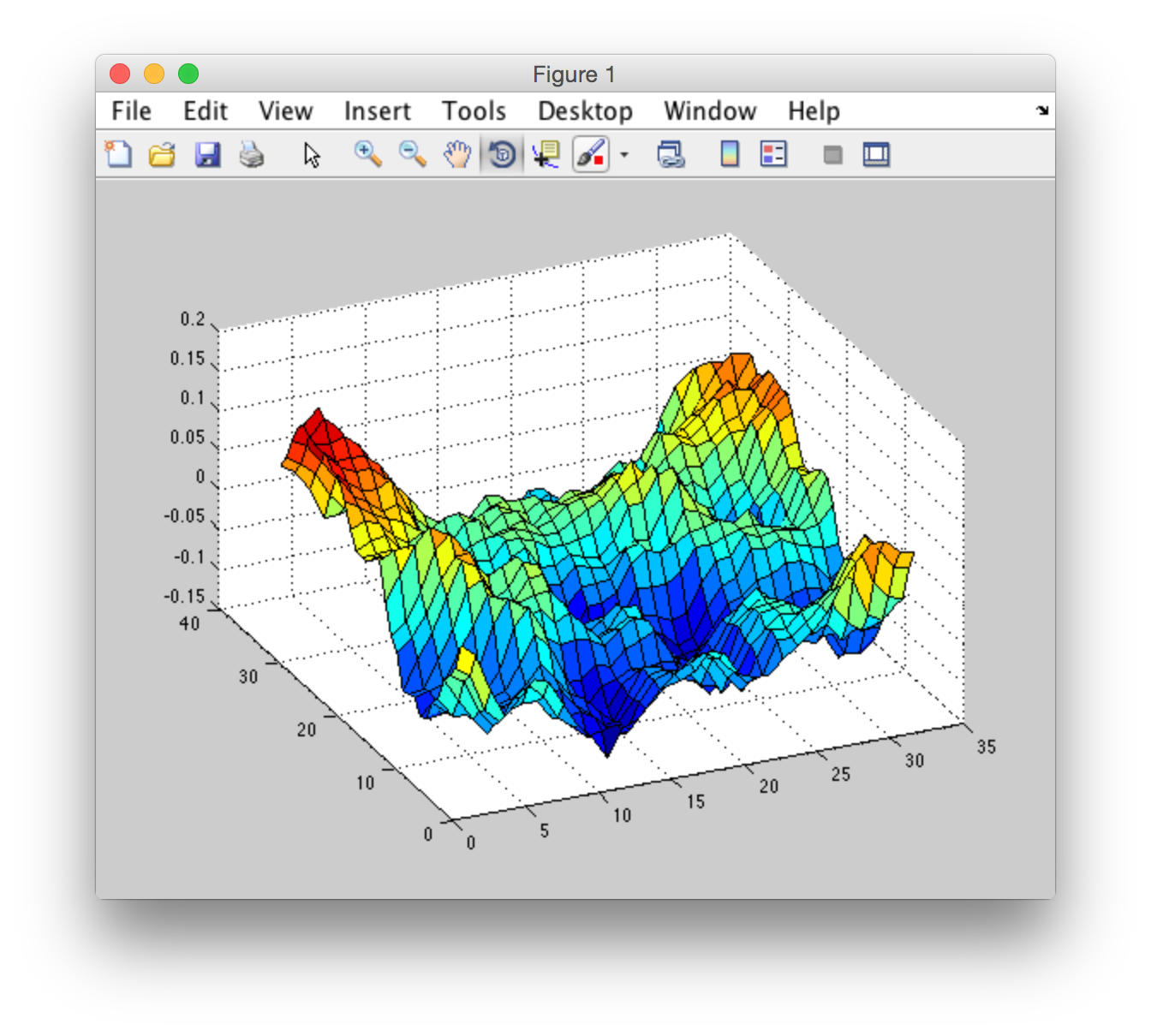
Matlab ifft:
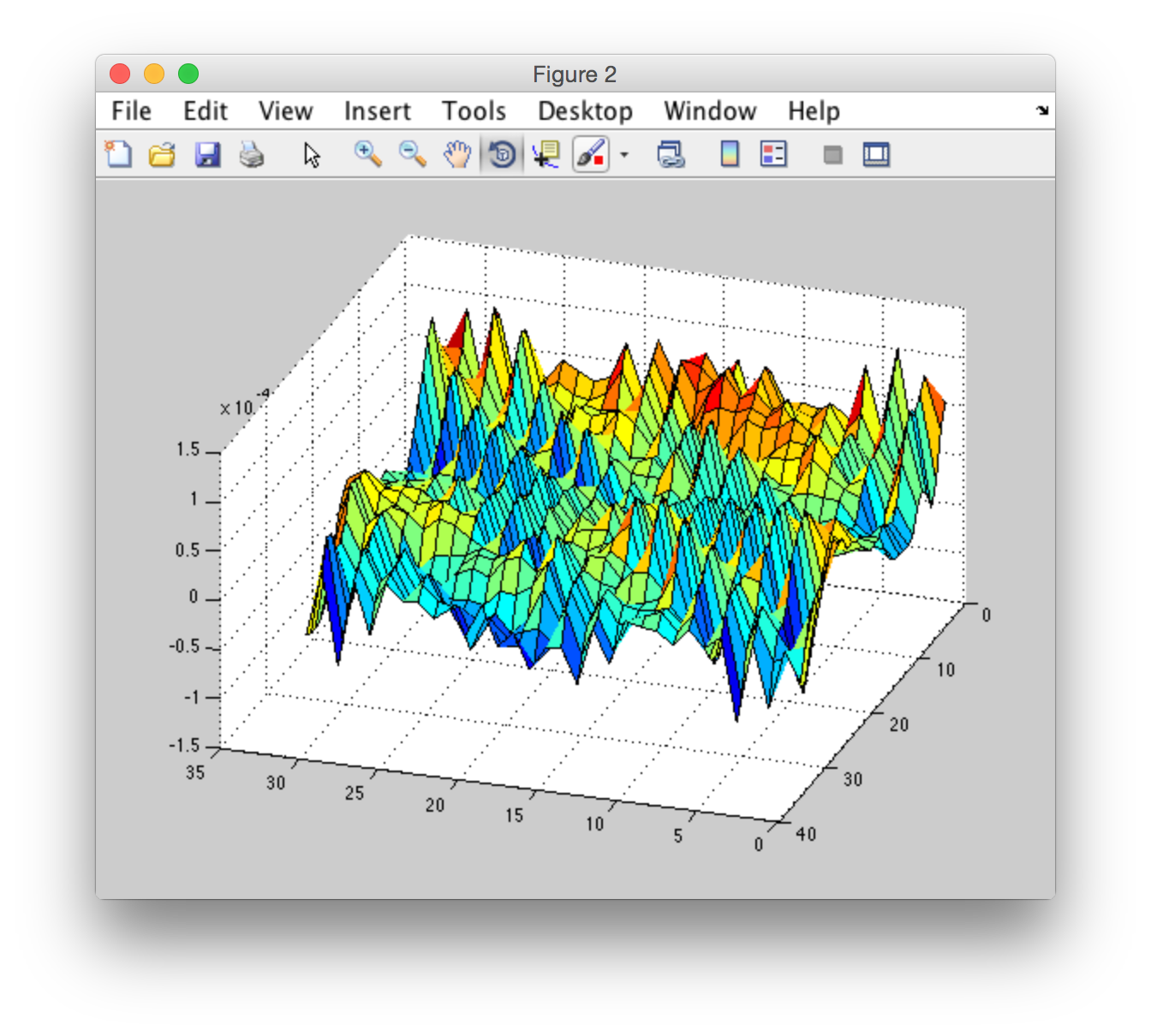
либо я не понимаю некоторые аспекты реализации cufftExecC2C или cufftExecC2C и matlab ifft-это разные алгоритмы с разными результатами.
кстати параметры для создания такой поверхности:
meshSize = 32
A = 1e-7
patchSize = 80
скорость ветра = 10
2 ответов
Ну, это было определенно забавное упражнение. Это полностью переписанный ответ, так как вы нашли проблемы, о которых вы спрашивали сами.
вместо удаления моего ответа, есть еще заслуга в публикации, чтобы помочь вам векторизовать и / или объяснить несколько бит кода.
я полностью переписал GUI, который я дал в своем предыдущем ответе, чтобы включить ваши изменения и добавить пару опций. Он начал расти руки и ноги, поэтому я не буду помещать список здесь но вы можете найти полный файл там:
это полностью автономно и включает в себя все вычислительные функции, которые я векторизовал и список отдельно ниже.
GUI позволит вам играть с параметрами, анимировать волны, экспортировать GIF-файл (и несколько других опций, таких как "предустановка", но они еще не слишком сглажены). Несколько примеров того, что вы можете достичь:
Basic
это то, что вы получаете с быстрыми настройками по умолчанию и несколькими параметрами рендеринга. Это использует небольшой размер сетки и быстрый шаг времени, поэтому он работает довольно быстро на любой машине.

я довольно ограничен дома (Pentium E2200 32bit), поэтому я мог практиковать только с ограниченными настройками. Gui будет работать даже с максимальными настройками, но он станет медленным, чтобы действительно наслаждаться.
однако, с быстрым запуском ocean_simulator на работе (i7 64 бит, 8 ядер, 16 ГБ оперативной памяти, 2xSSD в Raid), это делает его намного веселее! Вот несколько примеров:
хотя это сделано на гораздо лучшей машине, я не использовал никаких параллельных функций и никаких вычислений GPU, поэтому Matlab использовал только часть этих спецификаций, что означает, что он, вероятно, может работать так же хорошо на любой 64-битной системе с приличной ОЗУ
или озеро
это довольно плоская поверхность воды, как озеро. Даже сильные ветры не производят волн высокой амплитуды (но все же много мини-вейвлетов). Если вы ветер серфер, глядя на это из окна на вершине холма, ваше сердце собирается пропустить удар, и ваш следующий шаг, чтобы позвонить Дейв"человек! ускорять. встретимся в пять на вода!"

зыбь
это вы смотрите с моста вашей лодки утром, после того, как боролись с бурей всю ночь. Шторм рассеялся, и длинные большие волны являются последним свидетелем того, что было определенно шаткой ночью (люди с опытом плавания будут знать ...).

Т-Буря
и это было то, что вы были до ночи до...

 второй gif сделан дома, следовательно, отсутствие деталей ... жаль
второй gif сделан дома, следовательно, отсутствие деталей ... жаль
в самом низу:
наконец, gui позволит вам добавить патч вокруг водного домена. В gui он прозрачен, поэтому вы можете добавлять объекты под водой или хорошее дно океана. К сожалению, формат GIF не может включать альфа-канал, поэтому здесь нет прозрачности (но если вы экспортируете видео, вы должны быть ладно.)
кроме того, экспорт в GIF ухудшает изображение, соединение между границей домена и поверхностью воды безупречно, если вы запустите это в Matlab. В некоторых случаях это также заставляет Matlab ухудшать рендеринг освещения, поэтому это определенно не лучший вариант для экспорта, но он позволяет больше вещей играть в matlab.

теперь на код:
вместо перечисления полного GUI, который был бы очень длинным (этот пост длинный достаточно уже), я просто перечислю здесь переписанную версию код код, и объяснить изменения.
вы должны заметить массовое увеличение скорости выполнения (порядки величины), благодаря оставшейся векторизации, но в основном по двум причинам:
i)многие расчеты были повторены. Кэширование значений и их повторное использование намного быстрее, чем пересчет полных матриц в циклах (во время анимации).
(ii) обратите внимание, как я определил поверхность графический объект. Он определяется только один раз (пустой даже), затем все дальнейшие вызовы (в цикле) обновляют только базовый ZData объекта поверхности (вместо повторного создания объекта поверхности на каждой итерации.
вот:
%% // clear workspace
clear all; close all; clc;
%% // Default parameters
param.meshsize = 128 ; %// main grid size
param.patchsize = 200 ;
param.windSpeed = 100 ; %// what unit ? [m/s] ??
param.winddir = 90 ; %// Azimuth
param.rng = 13 ; %// setting seed for random numbers
param.A = 1e-7 ; %// Scaling factor
param.g = 9.81 ; %// gravitational constant
param.xLim = [-10 10] ; %// domain limits X
param.yLim = [-10 10] ; %// domain limits Y
param.zLim = [-1e-4 1e-4]*2 ;
gridSize = param.meshsize * [1 1] ;
%% // Define the grid X-Y domain
x = linspace( param.xLim(1) , param.xLim(2) , param.meshsize ) ;
y = linspace( param.yLim(1) , param.yLim(2) , param.meshsize ) ;
[X,Y] = meshgrid(x, y);
%% // get the grid parameters which remain constants (not time dependent)
[H0, W, Grid_Sign] = initialize_wave( param ) ;
%% // calculate wave at t0
t0 = 0 ;
Z = calc_wave( H0 , W , t0 , Grid_Sign ) ;
%% // populate the display panel
h.fig = figure('Color','w') ;
h.ax = handle(axes) ; %// create an empty axes that fills the figure
h.surf = handle( surf( NaN(2) ) ) ; %// create an empty "surface" object
%% // Display the initial wave surface
set( h.surf , 'XData',X , 'YData',Y , 'ZData',Z )
set( h.ax , 'XLim',param.xLim , 'YLim',param.yLim , 'ZLim',param.zLim )
%% // Change some rendering options
axis off %// make the axis grid and border invisible
shading interp %// improve shading (remove "faceted" effect)
blue = linspace(0.4, 1.0, 25).' ; cmap = [blue*0, blue*0, blue]; %'// create blue colormap
colormap(cmap)
%// configure lighting
h.light_handle = lightangle(-45,30) ; %// add a light source
set(h.surf,'FaceLighting','phong','AmbientStrength',.3,'DiffuseStrength',.8,'SpecularStrength',.9,'SpecularExponent',25,'BackFaceLighting','unlit')
%% // Animate
view(75,55) %// no need to reset the view inside the loop ;)
timeStep = 1./25 ;
nSteps = 2000 ;
for time = (1:nSteps)*timeStep
%// update wave surface
Z = calc_wave( H0,W,time,Grid_Sign ) ;
h.surf.ZData = Z ;
pause(0.001);
end
%% // This block of code is only if you want to generate a GIF file
%// be carefull on how many frames you put there, the size of the GIF can
%// quickly grow out of proportion ;)
nFrame = 55 ;
gifFileName = 'MyDancingWaves.gif' ;
view(-70,40)
clear im
f = getframe;
[im,map] = rgb2ind(f.cdata,256,'nodither');
im(1,1,1,20) = 0;
iframe = 0 ;
for time = (1:nFrame)*.5
%// update wave surface
Z = calc_wave( H0,W,time,Grid_Sign ) ;
h.surf.ZData = Z ;
pause(0.001);
f = getframe;
iframe= iframe+1 ;
im(:,:,1,iframe) = rgb2ind(f.cdata,map,'nodither');
end
imwrite(im,map,gifFileName,'DelayTime',0,'LoopCount',inf)
disp([num2str(nFrame) ' frames written in file: ' gifFileName])
вы заметите, что я изменил несколько вещей, но я могу заверить вас, что расчеты точно такие же. Этот код вызывает несколько подфункций, но все они векторные, поэтому, если вы хотите, вы можете просто скопировать/вставить их сюда и бегут все рядные.
первая вызванная функция initialize_wave.m
все рассчитанное здесь будет постоянным позже (оно не меняется со временем, когда вы позже анимируете волны), поэтому имело смысл поместить это в блок самостоятельно.
function [H0, W, Grid_Sign] = initialize_wave( param )
% function [H0, W, Grid_Sign] = initialize_wave( param )
%
% This function return the wave height coefficients H0 and W for the
% parameters given in input. These coefficients are constants for a given
% set of input parameters.
% Third output parameter is optional (easy to recalculate anyway)
rng(param.rng); %// setting seed for random numbers
gridSize = param.meshsize * [1 1] ;
meshLim = pi * param.meshsize / param.patchsize ;
N = linspace(-meshLim , meshLim , param.meshsize ) ;
M = linspace(-meshLim , meshLim , param.meshsize ) ;
[Kx,Ky] = meshgrid(N,M) ;
K = sqrt(Kx.^2 + Ky.^2); %// ||K||
W = sqrt(K .* param.g); %// deep water frequencies (empirical parameter)
[windx , windy] = pol2cart( deg2rad(param.winddir) , 1) ;
P = phillips(Kx, Ky, [windx , windy], param.windSpeed, param.A, param.g) ;
H0 = 1/sqrt(2) .* (randn(gridSize) + 1i .* randn(gridSize)) .* sqrt(P); % height field at time t = 0
if nargout == 3
Grid_Sign = signGrid( param.meshsize ) ;
end
обратите внимание, что начальный winDir параметр теперь выражается одним скалярным значением, представляющим "Азимут" (в степени) ветра (от 0 до 360). Это позже переведено на свой X и Y компоненты благодаря функции pol2cart.
[windx , windy] = pol2cart( deg2rad(param.winddir) , 1) ;
это гарантирует, что норма всегда 1.
функция вызывает ваши проблемные phillips.m отдельно, но, как уже было сказано, он работает даже полностью векторизованный, поэтому вы можете скопировать его обратно в строку, если хотите. (не волнуйтесь, я проверил результаты против ваших версий = > строго идентичные). Обратите внимание, что эта функция не выводит комплексные числа, поэтому не было необходимости сравнивать воображаемые части.
function P = phillips(Kx, Ky, windDir, windSpeed, A, g)
%// The function now accept scalar, vector or full 2D grid matrix as input
K_sq = Kx.^2 + Ky.^2;
L = windSpeed.^2 ./ g;
k_norm = sqrt(K_sq) ;
WK = Kx./k_norm * windDir(1) + Ky./k_norm * windDir(2);
P = A ./ K_sq.^2 .* exp(-1.0 ./ (K_sq * L^2)) .* WK.^2 ;
P( K_sq==0 | WK<0 ) = 0 ;
end
следующая функция, вызываемая основной программой, -calc_wave.m. Эта функция завершает вычисления волнового поля за данное время. Определенно стоит иметь это самостоятельно, потому что это набор вычислений mimimun, который придется повторять для каждого заданного времени, когда вы хотите оживить волны.
function Z = calc_wave( H0,W,time,Grid_Sign )
% Z = calc_wave( H0,W,time,Grid_Sign )
%
% This function calculate the wave height based on the wave coefficients H0
% and W, for a given "time". Default time=0 if not supplied.
% Fourth output parameter is optional (easy to recalculate anyway)
% recalculate the grid sign if not supplied in input
if nargin < 4
Grid_Sign = signGrid( param.meshsize ) ;
end
% Assign time=0 if not specified in input
if nargin < 3 ; time = 0 ; end
wt = exp(1i .* W .* time ) ;
Ht = H0 .* wt + conj(rot90(H0,2)) .* conj(wt) ;
Z = real( ifft2(Ht) .* Grid_Sign ) ;
end
последние 3 строки расчетов требует немного объяснения, поскольку они получили самые большие изменения (все для того же результата, но гораздо лучшей скорости).
Ваша исходная строка:
Ht = H0 .* exp(1i .* W .* (t * timeStep)) + conj(flip(flip(H0,1),2)) .* exp(-1i .* W .* (t * timeStep));
пересчитать то же самое слишком много раз, чтобы быть эффективным:
(t * timeStep) рассчитывается дважды на линии, в каждом цикле, в то время как легко получить правильный time значение для каждой строки, когда time инициализируется в начале цикла for time = (1:nSteps)*timeStep.
Также обратите внимание, что exp(-1i .* W .* time) это то же самое, чем conj(exp(1i .* W .* time)). Вместо того, чтобы делать 2*m*n умножения, чтобы вычислить их каждый, быстрее вычислить один раз, а затем использовать conj() операция, которая намного быстрее.
Таким образом, ваша единственная строка станет:
wt = exp(1i .* W .* time ) ;
Ht = H0 .* wt + conj(flip(flip(H0,1),2)) .* conj(wt) ;
последнее незначительное касание,flip(flip(H0,1),2)) можно заменить на rot90(H0,2) (еще немного быстрее).
заметим, что функция calc_wave будет повторено обширно, определенно стоит уменьшить количество вычислений (как мы сделали выше), но также посылаю ему Grid_Sign параметр (вместо того, чтобы позволить функции пересчитывать его каждую итерацию). Вот почему:--56-->
ваша загадочная функция signCor(ifft2(Ht),meshSize)), просто переверните знак каждого другого элемента Ht. Существует более быстрый способ достижения этого: просто умножьте Ht матрицей того же размера (Grid_Sign), которая является матрицей чередовались +1 -1 ... и так далее.
так signCor(ifft2(Ht),meshSize) становится ifft2(Ht) .* Grid_Sign.
С Grid_Sign зависит только от размер матрицы, он не меняется для каждого time в цикле вы вычисляете его только один раз (перед циклом), а затем используете его как для каждой другой итерации. Он рассчитывается следующим образом (векторизованный, поэтому вы также можете поместить его в свой код):
function sgn = signGrid(n)
% return a matrix the size of n with alternate sign for every indice
% ex: sgn = signGrid(3) ;
% sgn =
% -1 1 -1
% 1 -1 1
% -1 1 -1
[x,y] = meshgrid(1:n,1:n) ;
sgn = ones( n ) ;
sgn(mod(x+y,2)==0) = -1 ;
end
наконец, вы заметите разницу в том, как сетки [Kx,Ky] определены между вашей версией и этой. Они дают немного другой результат, это просто вопрос выбора.
К объясните простым примером, давайте рассмотрим небольшой meshsize=5. Ваш способ делать вещи разделит ЭТО на 5 значений, равномерно расположенных, например:
Kx(first line)=[-1.5 -0.5 0.5 1.5 2.5] * 2 * pi / patchSize
в то время как мой способ создания сетки будет производить одинаково разнесенные значения, но также сосредоточены на границах домена, например:
Kx(first line)=[-2.50 -1.25 0.0 1.25 2.50] * 2 * pi / patchSize
кажется, больше уважать ваш комментарий % = 2*pi*n / Lx, -N/2 <= n < N/2 в строке, где вы его определяете.
я предпочитаю симметричные решения (плюс это еще немного быстрее, но он рассчитывается только один раз, поэтому это не имеет большого значения), поэтому я использовал свой векторизованный способ, но это чисто вопрос выбора, вы можете определенно сохранить свой путь, он только слегка "смещает" всю матрицу результатов, но это не нарушает вычисления как таковые.
последние остатки первого ответа
Побочные Примечания программирования :
Я обнаруживаю, что вы пришли из мира или семьи C/C++. В Matlab вам не нужно определять десятичное число с кома (как 2.0, вы использовали это для большинства своих номеров). Если специально не определено иначе, Matlab по умолчанию приводит любое число к double, который является 64-битным типом с плавающей запятой. Так писать 2 * pi достаточно, чтобы получить максимальную точность (Matlab не будет использовать pi как целое число ; -)), вам не нужно писать 2.0 * pi. хотя он все равно будет работать, если вы не хотите менять свои привычки.
также ,( одно из большого преимущества Matlab), добавив . перед оператором обычно подразумевается "элементарная" операция. Вы можете добавить (.+), substract (.-), умножение (.*), разделить (./) полный элемент матрицы мудрый таким образом. Вот как я избавился от всех циклов в вашем коде. Это также работает для оператора питания:A.^2 вернет матрицу того же размера, что и A с каждым элементом в квадрате.
здесьрабочая программа.
прежде всего-исходный код:
clear all; close all; clc;
rng(13); % setting seed for random numbers
meshSize = 128; % field size
windDir = [0.1,1];
patchSize = 200;
A = 1e-7;
g = 9.81; % gravitational constant
windSpeed = 100;
timeStep = 1/25;
x1 = linspace(-10, 10, meshSize+1); x = x1(1:meshSize);
y1 = linspace(-10, 10, meshSize+1); y = y1(1:meshSize);
[X,Y] = meshgrid(x,y); % wave field
i = 1:meshSize; j = 1:meshSize; % indecies
[I,J] = meshgrid(i,j); % field of indecies
Kx = 2.0 * pi / patchSize * (-meshSize / 2.0 + I); % = 2*pi*n / Lx, -N/2 <= n < N/2
Ky = 2.0 * pi / patchSize * (-meshSize / 2.0 + J); % = 2*pi*m / Ly, -M/2 <= m < M/2
K = sqrt(Kx.^2 + Ky.^2); % ||K||
W = sqrt(K .* g); % deep water frequencies (empirical parameter)
P = zeros(size(X)); % Cant compute P without loops
for i = 1:meshSize
for j = 1:meshSize
P(i,j) = phillips(Kx(i,j), Ky(i,j), windDir, windSpeed, A, g); % phillips spectrum
end
end
H0 = 1/sqrt(2) .* (randn(size(X)) + 1i .* randn(size(X))) .* sqrt(P); % height field at time t = 0
rotate3d on;
for t = 1:10000 % 10000 * timeStep (sec)
Ht = H0 .* exp(1i .* W .* (t * timeStep)) + ...
conj(flip(flip(H0,1),2)) .* exp(-1i .* W .* (t * timeStep));
[az,el] = view;
surf(X,Y,real(signCor(ifft2(Ht),meshSize)));
axis([-10 10 -10 10 -1e-4 1e-4]); view(az,el);
blue = linspace(0.4, 1.0, 25)'; map = [blue*0, blue*0, blue];
%shading interp; % improve shading (remove "faceted" effect)
colormap(map);
pause(1/60);
end
Филлипс.m: (я попытался векторизовать вычисление спектра Филлипса, но столкнулся с трудностями, которые я покажу дальше)
function P = phillips(kx, ky, windDir, windSpeed, A, g)
k_sq = kx^2 + ky^2;
if k_sq == 0
P = 0;
else
L = windSpeed^2 / g;
k = [kx, ky] / sqrt(k_sq);
wk = k(1) * windDir(1) + k(2) * windDir(2);
P = A / k_sq^2 * exp(-1.0 / (k_sq * L^2)) * wk^2;
if wk < 0
P = 0;
end
end
end
signCor.м.: (Эта функция для меня абсолютно загадка... Я скопировал его из реализации "CUDA FFT Ocean Simulation". Без него симуляция работает гораздо хуже. И снова я не знаю, как векторизовать этот функция.)
function H = signCor(H1, meshSize)
H = H1;
for i = 1:meshSize
for j = 1:meshSize
if mod(i+j,2) == 0
sign = -1; % works fine if we change signs vice versa
else
sign = 1;
end
H(i,j) = H1(i,j) * sign;
end
end
end
самая большая ошибка, которую я сделал, это то, что я использовал ifft вместо ifft2, вот почему CUDA ifft и Matlab ifft не совпали.
моя вторая ошибка была в эти строки кода:
kx = 2.0 * pi / patchSize * (-meshSize / 2.0 + x(i)); % = 2*pi*n / Lx
ky = 2.0 * pi / patchSize * (-meshSize / 2.0 + y(j)); % = 2*pi*m / Ly
надо было написать:
kx = 2.0 * pi / patchSize * (-meshSize / 2.0 + i); % = 2*pi*n / Lx
ky = 2.0 * pi / patchSize * (-meshSize / 2.0 + j); % = 2*pi*m / Ly
я немного поиграл с параметрами A, meshSize, patchSize и пришел к выводу, что:
как-то правдоподобный параметр амплитуды волны A * (patchSize / meshSize), где A-это не что иное, как коэффициент масштабирования.
для 'спокойная'
patchSize / meshSize <= 0.5.для 'цунами'
patchSize / meshSize >= 3.0.
трудности с векторизацией спектра Филлипса:
у меня есть 2 функции:
% non-vectorized spectrum
function P = phillips1(kx, ky, windDir, windSpeed, A, g)
k_sq = kx^2 + ky^2;
if k_sq == 0
P = 0;
else
L = windSpeed^2 / g;
k = [kx, ky] / sqrt(k_sq);
wk = k(1) * windDir(1) + k(2) * windDir(2);
P = A / k_sq^2 * exp(-1.0 / (k_sq * L^2)) * wk^2;
if wk < 0
P = 0;
end
end
end
% vectorized spectrum
function P = phillips2(Kx, Ky, windDir, windSpeed, A, g)
K_sq = Kx .^ 2 + Ky .^ 2;
L = -g^2 / windSpeed^4;
WK = (Kx ./ K_sq) .* windDir(1) + (Ky ./ K_sq) .* windDir(2);
P = (A ./ (K_sq .^ 2)) .* ( exp(L ./ K_sq) .* (WK .^ 2) );
P(K_sq == 0) = 0;
P(WK < 0) = 0;
P(isinf(P)) = 0;
end
после того, как я вычислить P1 используя phillips1 и P2 используя phillips2 я сюжет их разница:
subplot(2,1,1); surf(X,Y,real(P2-P1)); title('Difference in real part');
subplot(2,1,2); surf(X,Y,imag(P2-P1)); title('Difference in imaginary part');
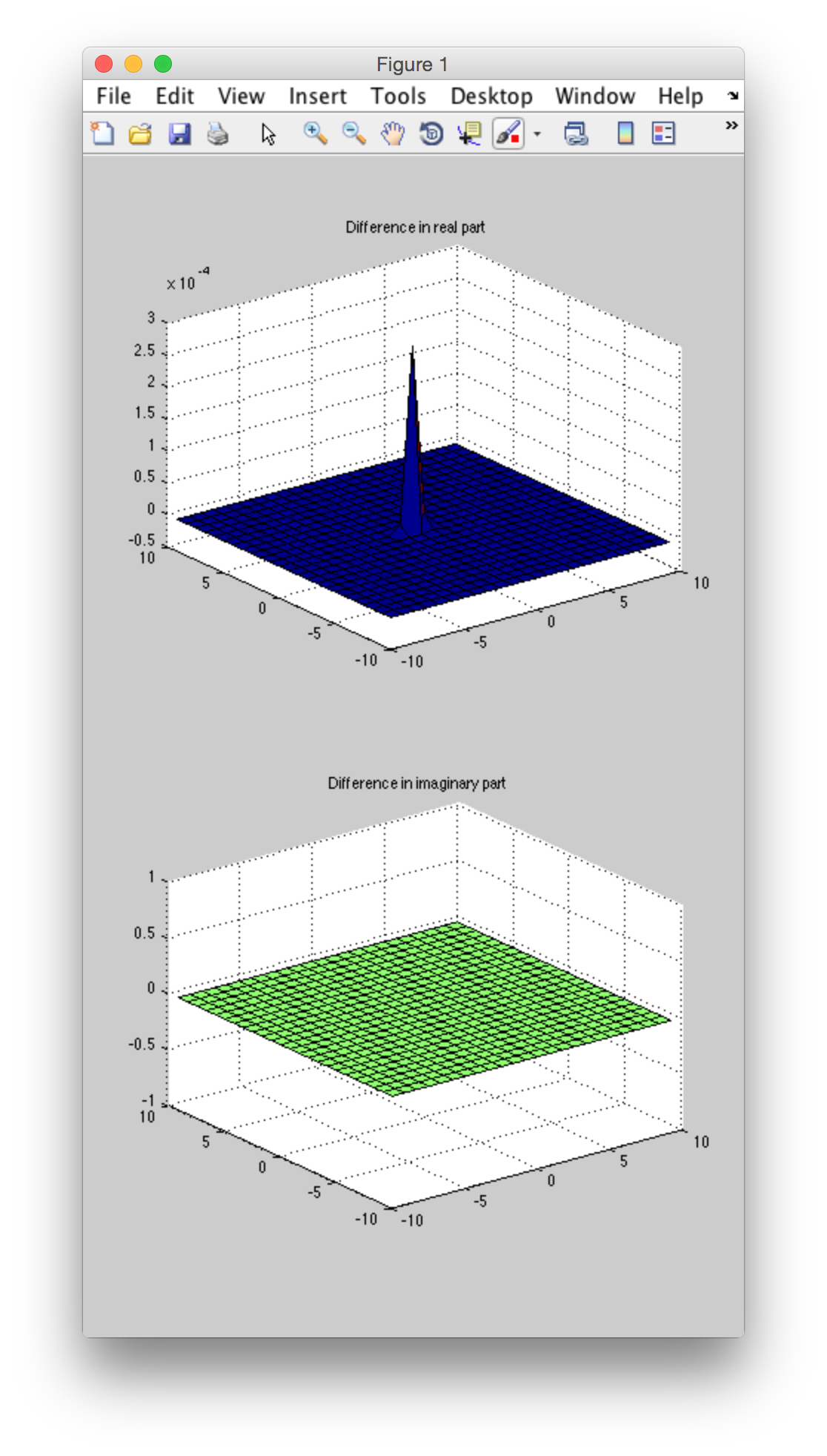
это прекрасно иллюстрирует, что существует огромная разница между этими 2 спектрами в реальной части.
