Matlab: решение логарифмического уравнения

у меня есть следующее уравнение, которое я хочу решить относительно a:

x = (a-b-c+d)/log((a-b)/(c-d))

здесь x, b, c и d известны. Я использовал Wolfram Alpha для решения уравнения, и результат:

a = b-x*W(-((c-d)*exp(d/x-c/x))/x)

здесь W является функцией журнала продукта (функция Lambert W). Возможно, будет легче увидеть его в страница Вольфрам Альфа.

я использовал встроенный Matlab чтобы решить уравнение. Это довольно медленно и является узким местом в моем сценарии. Есть ли другой, более быстрый способ сделать это? Он не должен быть точным вплоть до десятичного знака.

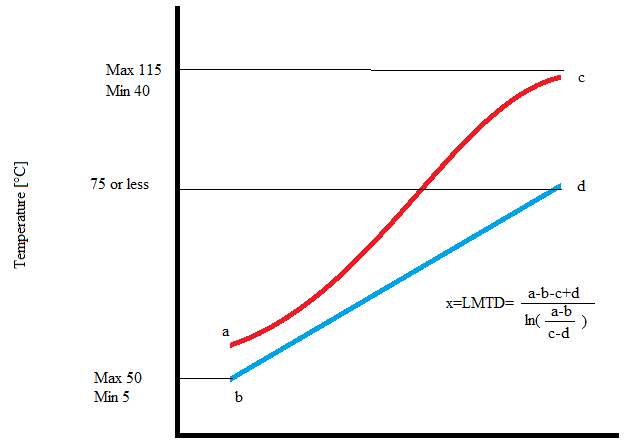
изменить: Я понятия не имел, что это уравнение так трудно решить. Вот картина, иллюстрирующая мою проблему. Температуры b-d плюс LMTD меняют в каждом шаге времени, но знаны. Тепло передается от красной линии (CO2) к Голубой линии (вода). Мне нужно найти температуру "а". Я не знал, что это так трудно. рассчитать! :P enter image description here

7
logarithm matlab natural-logarithm wolframalpha

2 ответов

другой вариант основан на более простой функция ω Райта:

a = b - x.*wrightOmega(log(-(c-d)./x) - (c-d)./x);

предусмотрено, что d ~= c + x.*wrightOmega(log(-(c-d)./x) - (c-d)./x) (т. е. d ~= c+b-a, x is 0/0 в данном случае). Это эквивалентно основной ветви Ламберт W функции, W0, который, я думаю, является ветвью решения, которую вы хотите.

как lambertW, есть wrightOmega

4

два (комбинируются) параметры:

  • ваш сценарий уже векторизован? Оцените функцию для более чем одного аргумента. Выполнение for i = 1:100, a(i)=lambertw(rhs(i)); end медленнее, чем a=lambertw(rhs).
  • если вы имеете дело с реальной ценной ветвью LambertW (т. е. ваши аргументы находятся в интервале [-1/e, inf) ), вы можете использовать реализацию Lambert_W, представленного Клив Молер на Обмен.
1