Matlab, создайте и постройте облако точек, распределенное внутри треугольника

Я пытаюсь создать облако 2D точек (равномерно), распределенных внутри треугольника. До сих пор я достиг следующего:

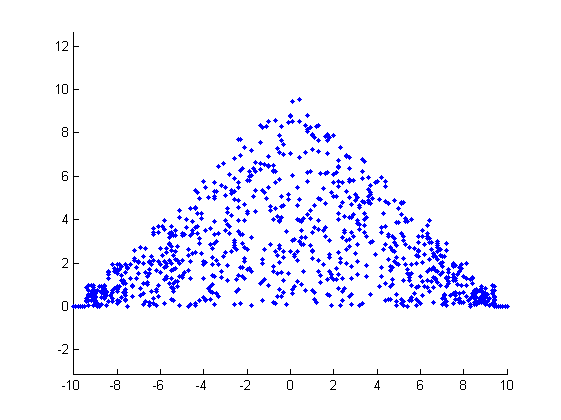
Matlab plot

код, который я использовал, таков:

N = 1000;
X = -10:0.1:10;
for i=1:N
    j = ceil(rand() * length(X));
    x_i = X(j);
    y_i = (10 - abs(x_i)) * rand;

    E(:, i) = [x_i y_i];
end

однако точки распределены неравномерно, что хорошо видно в левом и правом углах. Как я могу улучшить этот результат? Я тоже пытался найти разные формы, но безуспешно.

6
matlab random uniform

4 ответов

сначала вы должны спросить себя, что сделает точки внутри треугольника распределенными равномерно.

чтобы сделать длинную историю короткой, учитывая все три вершины треугольника, вам нужно преобразовать два равномерно распределенных случайных значения следующим образом:

N = 1000;                    % # Number of points
V = [-10, 0; 0, 10; 10, 0];  % # Triangle vertices, pairs of (x, y)
t = sqrt(rand(N, 1));
s = rand(N, 1);
P = (1 - t) * V(1, :) + bsxfun(@times, ((1 - s) * V(2, :) + s * V(3, :)), t);

в результате получится набор точек, которые равномерно распределены внутри указанного треугольника:

scatter(P(:, 1), P(:, 2), '.')

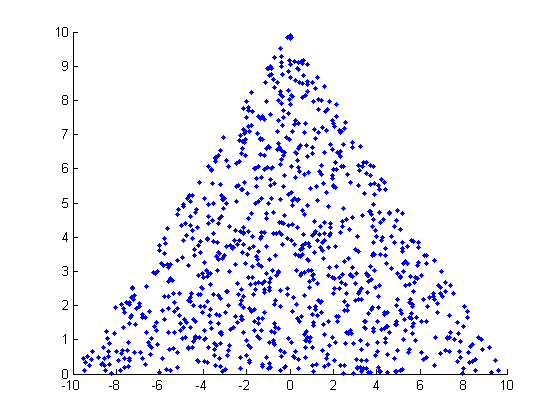
enter image description here

обратите внимание, что это решение не включает повторное условная манипуляция случайными числами, поэтому она не может потенциально попасть в бесконечный цикл.

для дальнейшего чтения, посмотрите на в этой статье.

9

эта концентрация точек будет ожидаться от того, как вы строите точки. Ваши точки равномерно распределены по оси X. В крайних точках треугольника имеется примерно такое же количество точек в центре треугольника, но они распределены вдоль гораздо меньшей области.

первый и лучший подход, который я могу придумать:грубую силу. Распределите точки поровну вокруг большей области, а затем удалите те это за пределами интересующего Вас региона.

N = 1000;
points = zeros(N,2);
n = 0;
while (n < N)
    n = n + 1;
    x_i = 20*rand-10; % generate a number between -10 and 10
    y_i = 10*rand; % generate a number between 0 and 10
    if (y_i > 10 - abs(x_i)) % if the points are outside the triangle
       n = n - 1; % decrease the counter to try to generate one more point
    else % if the point is inside the triangle
       points(n,:) = [x_i y_i]; % add it to a list of points
    end
end

% plot the points generated
plot(points(:,1), points(:,2), '.');
title ('1000 points randomly distributed inside a triangle');

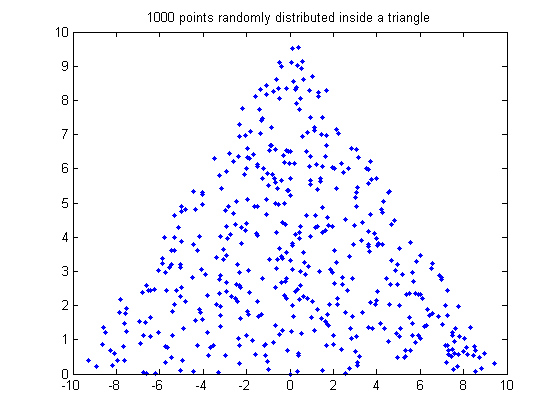
результат кода, который я опубликовал: Plot generated by the code above

один важный отказ от ответственности: случайное распределение не означает "равномерно" распределено! Если вы генерируете данные случайным образом из равномерного распределения, это не означает, что он будет" равномерно распределен " по треугольнику. На самом деле вы увидите несколько групп точек.

2

вы можете представить, что треугольник разделен вертикально на две половины, и переместите одну половину так, чтобы вместе с другой она образует прямоугольник. Теперь вы пробуете равномерно в прямоугольнике, что легко, а затем перемещаете половину треугольника назад.

кроме того, проще работать с единицами длины (прямоугольник становится квадратом), а затем растянуть треугольник до нужных размеров.

x = [-10 10]; % //triangle base
y = [0 10]; % //triangle height
N = 1000; %// number of points

points = rand(N,2); %// sample uniformly in unit square
ind = points(:,2)>points(:,1); %// points to be unfolded 
points(ind,:) = [2-points(ind,2) points(ind,1)]; %// unfold them
points(:,1) = x(1) + (x(2)-x(1))/2*points(:,1); %// stretch x as needed
points(:,2) = y(1) + (y(2)-y(1))*points(:,2); %// stretch y as needed
plot(points(:,1),points(:,2),'.')

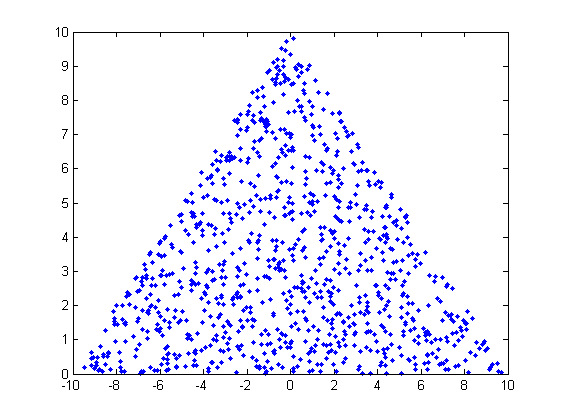
enter image description here

1

мы можем обобщить это дело. Если вы хотите взять образцы точек из некоторого (n - 1)-мерного симплекса в евклидовом пространстве равномерно (не обязательно треугольник - это может быть любой выпуклый многогранник), просто возьмите вектор из симметричного n-мерного распределения Дирихле с параметром 1 - это выпуклые (или барицентрические) координаты относительно вершин многогранника.

0