минимизация многомерной дифференцируемой функции с помощью scipy.оптимизировать

Я пытаюсь свести к минимуму следующую функцию с помощью scipy.optimize:

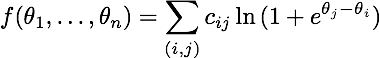
enter image description here

чей градиент таков:

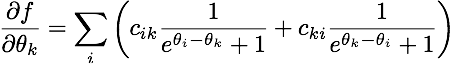
enter image description here

(для тех, кто заинтересован, это функция правдоподобия модели Брэдли-Терри-Люса для попарных сравнений. Очень тесно связан с логистической регрессией.)

довольно ясно, что добавление константы ко всем параметрам не изменяет значение функции. Следовательно, я позволяю theta_1 = 0. Вот реализация целевых функций и градиента в python (theta становится x здесь):

def objective(x):
    x = np.insert(x, 0, 0.0)
    tiles = np.tile(x, (len(x), 1))
    combs = tiles.T - tiles
    exps = np.dstack((zeros, combs))
    return np.sum(cijs * scipy.misc.logsumexp(exps, axis=2))

def gradient(x):
    zeros = np.zeros(cijs.shape)
    x = np.insert(x, 0, 0.0)
    tiles = np.tile(x, (len(x), 1))
    combs = tiles - tiles.T
    one = 1.0 / (np.exp(combs) + 1)
    two = 1.0 / (np.exp(combs.T) + 1)
    mat = (cijs * one) + (cijs.T * two)
    grad = np.sum(mat, axis=0)
    return grad[1:]  # Don't return the first element

вот пример cijs может выглядеть так:

[[ 0  5  1  4  6]
 [ 4  0  2  2  0]
 [ 6  4  0  9  3]
 [ 6  8  3  0  5]
 [10  7 11  4  0]]

это код, который я запускаю для выполнения минимизации:

x0 = numpy.random.random(nb_items - 1)
# Let's try one algorithm...
xopt1 = scipy.optimize.fmin_bfgs(objective, x0, fprime=gradient, disp=True)
# And another one...
xopt2 = scipy.optimize.fmin_cg(objective, x0, fprime=gradient, disp=True)

однако он всегда терпит неудачу на первой итерации:

Warning: Desired error not necessarily achieved due to precision loss.
         Current function value: 73.290610
         Iterations: 0
         Function evaluations: 38
         Gradient evaluations: 27

Я не могу понять, почему он терпит неудачу. Из-за этого отображается ошибка линия: https://github.com/scipy/scipy/blob/master/scipy/optimize/optimize.py#L853

7
mathematical-optimization numpy python scipy

2 ответов

As @pv. в качестве комментария я сделал ошибку в вычислении градиента. Прежде всего, правильное (математическое) выражение для градиента моей целевой функции:

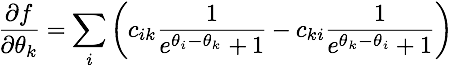
enter image description here

(обратите внимание на знак "минус".) Кроме того, моя реализация Python была полностью неправильной, за пределами ошибки знака. Вот мой обновленный градиент:

def gradient(x):
    nb_comparisons = cijs + cijs.T
    x = np.insert(x, 0, 0.0)
    tiles = np.tile(x, (len(x), 1))
    combs = tiles - tiles.T
    probs = 1.0 / (np.exp(combs) + 1)
    mat = (nb_comparisons * probs) - cijs
    grad = np.sum(mat, axis=1)
    return grad[1:]  # Don't return the first element.

чтобы отладить его, я использовал:

  • scipy.optimize.check_grad: показал, что моя функция градиента была получение результатов очень далеко от аппроксимированного (конечно-разностного) градиента.
  • scipy.optimize.approx_fprime чтобы получить представление о ценности должна выглядеть.
  • несколько отобранных вручную простых примеров, которые при необходимости можно было бы проанализировать вручную, и несколько запросов Wolfram Alpha для проверки здравомыслия.
2

Кажется, вы можете преобразовать его в (нелинейный) наименьших квадратов

1