нахождение минимального количества прямоугольных кусочков в прямоугольной плитке шоколада, с правилом
у меня проблемы с домашним заданием в школе. У меня есть шоколадная плитка, которая состоит из черных, белых или черно-белых (смешанных) квадратов. Я должен разделить его на две группы, в одной из которых есть только белые или черно-белые части, а в другой-только черные или черно-белые части. Разделять плитку шоколада значит трескать ее или горизонтально или вертикально вдоль линии которая отделяет индивидуальные квадраты.
учитывая макет шоколадного батончика, я должен найти оптимальное разделение, которое разделяет темные и белые кубики и приводит к наименьшему возможному количеству кусочков, шоколадная плитка не больше 50x50 квадратов.
шоколадная плитка определяется на стандартном входе, как это: первая строка состоит из двух целых чисел M (количество строк в шоколадке) и N (нет. столбцов), то есть m столбцов, каждый из которых состоит из N символов, символизирующих отдельные квадраты (0-черный, 1-белый, 2-смешанный)
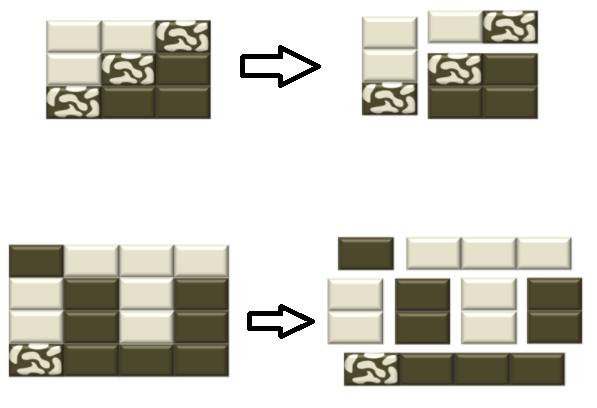
некоторые примеры оптимального дивизии, их входы соответственно (правильные выходы 3 и 7):
3 3
1 1 2
1 2 0
2 0 0
4 4
0 1 1 1
1 0 1 0
1 0 1 0
2 0 0 0
моя проблема в том, что мне удалось разработать решение, но алгоритм, который я использую, недостаточно быстр, если шоколадная плитка большая, например:
40 40
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 2 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 1 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 1 0 2 1 2 1 2 0 0 1 2 2 0 0 0 0 0 0 0 0 1 1 2 1 2 0 0 0 0 0 0 0 0 0 0
0 0 0 1 2 2 0 1 1 1 1 1 0 0 1 2 2 0 0 0 0 0 1 0 0 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 2 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1 1 2 2 0 0 0 1 2 2 1 2 1 0 0 0 0 0 1 2 1 2 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 2 2 1 2 0 0 0 0 0 2 1 2 2 0 0 0 0 0 2 1 2 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 2 2 2 1 1 0 0 0 0 0 2 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0
0 2 1 2 1 0 2 2 2 2 1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 2 0 2 2 1 0 0 0 0 0 0
0 2 2 1 2 0 1 2 2 1 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0
0 2 2 1 2 0 0 0 0 2 1 2 1 2 1 1 2 0 2 0 0 0 0 0 0 0 1 2 2 2 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 2 2 2 2 1 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0
0 0 0 0 0 0 0 0 0 1 2 1 1 2 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 2 2 0 0 0 0
0 0 0 0 0 0 0 2 1 2 0 0 2 2 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 1 1 0 0 0 0
0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 2 2 0 0 0 0
0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 2 2 1 0 0 0 0 2 0 1 1 1 2 1 2 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 2 1 2 2 2 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 1 2 1 1 2 2 0 0 0 0 0
0 0 0 0 0 0 1 2 1 2 2 1 0 0 0 0 0 0 0 1 2 1 2 0 0 0 0 0 0 0 0 0 2 1 2 0 0 0 0 0
0 0 0 0 0 0 1 2 2 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 0 0 0 0 2 1 1 0 0
0 0 0 0 0 0 1 1 1 1 1 2 2 0 0 0 0 0 0 0 0 1 1 1 2 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0
0 0 0 0 0 0 1 2 2 2 1 1 1 0 0 0 0 0 0 0 0 1 2 1 2 0 0 0 0 0 0 0 0 0 0 2 2 2 1 0
0 0 0 0 0 0 0 0 0 1 2 1 2 0 0 0 0 0 0 0 0 1 1 1 2 2 0 0 0 0 0 0 0 0 0 1 2 1 1 0
0 0 0 2 1 1 2 2 0 1 2 1 1 0 0 0 0 0 2 2 1 2 2 1 2 2 0 0 0 0 0 0 0 0 0 1 2 2 2 0
0 0 0 2 2 2 1 1 0 0 1 2 2 2 0 0 0 0 2 2 2 1 1 2 1 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 1 2 2 1 1 0 2 1 2 1 2 1 2 1 1 2 1 1 1 1 1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 2 2 2 2 1 0 1 1 1 1 1 1 2 1 1 2 2 1 0 1 2 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 0 0 2 1 1 1 2 1 2 0 0 1 2 1 2 1 2 2 0 0 0 0 0 0 0 1 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 2 2 1 1 2 2 1 1 1 1 1 1 1 2 1 0 0 0 0 0 0 0 2 2 2 0 0 0
0 0 0 0 0 0 0 1 1 1 2 0 0 1 1 1 2 2 1 2 2 2 1 0 0 0 1 1 1 0 0 0 0 0 1 2 1 0 0 0
0 0 0 0 0 0 0 2 1 1 2 0 0 0 0 0 0 2 2 2 1 1 1 0 0 0 1 2 2 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 2 2 2 2 0 0 0 0 0 0 2 1 1 1 2 0 0 0 0 1 2 2 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 1 1 2 0 2
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 0 0 0 0 0 0 0 1 2 1 0 0
0 0 0 0 0 0 0 0 0 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 0 0 0 0 0 0 0 1 2 1 0 0
0 0 0 0 0 0 0 0 0 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
тогда для моей программы требуется 10 секунд, чтобы решить его (правильное решение для этого-126, и я должен быть в состоянии решить его менее чем за 2 секунды!)
мой алгоритм работает примерно с некоторой незначительной оптимизацией, такой как это: повторите все возможные линии, где можно вырезать, а затем рекурсивно сделайте то же самое для 2 новых прямоугольников, если они больше не могут быть разделены, а затем верните 1.
функция после итерации через все возможные сокращения всегда возвращает минимум, как только минимум будет найден, затем сохраните его, и если мне придется снова решить этот прямоугольник, просто верните значение.
Я подумал, что, может быть, если Я уже решил конкретный прямоугольник, и теперь мне нужно решить тот, который на одну строку или столбец больше или меньше, тогда я мог бы как-то использовать решение, которое у меня уже есть для этого, и использовать его для нового. Но я действительно не знаю, как бы я реализовал такую функцию. Сейчас мой алгоритм рассматривает его как совершенно новый нераскрытый прямоугольник.
мой код до сих пор:
#include <stdio.h>
#include <stdlib.h>
unsigned int M, N;
unsigned int ****pieces; ////already solved rectangles, the value of pieces[y0][x0][y1][x1] is the optimal number of pieces in which the particular rectangle(that has upperleft corner in [x0,y0] and bottomright corner in[x1,y1]) can be divided
int ****checked;
unsigned int inf;
unsigned int minbreaks(int mat[M][N], unsigned int starti, unsigned int startj, unsigned int maxi, unsigned int maxj) {
if (pieces[starti][startj][maxi][maxj] != 0) {
return pieces[starti][startj][maxi][maxj];
} else {
unsigned int vbreaks[maxj - 1];
unsigned int hbreaks[maxi - 1];
for (unsigned int i = 0; i < maxj - 1; i++) {
vbreaks[i] = inf;
}
for (unsigned int i = 0; i < maxi - 1; i++) {
hbreaks[i] = inf;
}
unsigned int currentmin = inf;
for (unsigned int i = starti; i < maxi; i++) {
for (unsigned int j = startj; j < maxj - 1; j++) {
if (mat[i][j] != 2) {
for (unsigned int k = startj + 1; k < maxj; k++) {
if (vbreaks[k - 1] == inf) {
for (unsigned int z = starti; z < maxi; z++) {
if (!checked[i][j][z][k]) {
if (mat[z][k] != 2 && mat[i][j] != mat[z][k]) {
vbreaks[k - 1] = minbreaks(mat, starti, startj, maxi, k) + minbreaks(mat, starti, k, maxi, maxj);
if (vbreaks[k - 1] < currentmin) {
currentmin = vbreaks[k - 1];
}
break;
}
checked[i][j][z][k] = 1;
}
}
}
}
}
}
}
for (unsigned int i = starti; i < maxi - 1; i++) {
for (unsigned int j = startj; j < maxj; j++) {
if (mat[i][j] != 2) {
for (unsigned int k = starti + 1; k < maxi; k++) {
if (hbreaks[k - 1] == inf) {
for (unsigned int z = startj; z < maxj; z++) {
if (!checked[i][j][k][z]) {
if (mat[k][z] != 2 && mat[i][j] != mat[k][z]) {
hbreaks[k - 1] = minbreaks(mat, starti, startj, k, maxj) + minbreaks(mat, k, startj, maxi, maxj);
if (hbreaks[k - 1] < currentmin) {
currentmin = hbreaks[k - 1];
}
break;
}
checked[i][j][k][z] = 1;
}
}
}
}
}
}
}
if (currentmin == inf) {
currentmin = 1;
}
pieces[starti][startj][maxi][maxj] = currentmin;
return currentmin;
}
}
int main(void) {
FILE *file = stdin;
fscanf(file, "%u %u", &M, &N);
int mat[M][N];
pieces = malloc(sizeof (unsigned int***)*M);
checked = malloc(sizeof (int***)*M);
for (unsigned int i = 0; i < M; i++) {//initialize the pieces,checked and mat arrays.
pieces[i] = malloc(sizeof (unsigned int**)*N);
checked[i] = malloc(sizeof (int**)*N);
for (unsigned int j = 0; j < N; j++) {
int x;
fscanf(file, "%d", &x);
mat[i][j] = x;
pieces[i][j] = malloc(sizeof (unsigned int*)*(M + 1));
checked[i][j] = malloc(sizeof (int*)*M);
for (unsigned int y = i; y < M + 1; y++) {
pieces[i][j][y] = malloc(sizeof (unsigned int)*(N + 1));
for (unsigned int x = j; x < N + 1; x++) {
pieces[i][j][y][x] = 0;
}
}
for (unsigned int y = 0; y < M; y++) {
checked[i][j][y] = malloc(sizeof (int)*N);
for (unsigned int x = 0; x < N; x++) {
checked[i][j][y][x] = 0;
}
}
}
}
inf = M * N + 1; //number one bigger than maximal theoretically possible number of divisions
unsigned int result = minbreaks(mat, 0, 0, M, N);
printf("%un", result);
return (EXIT_SUCCESS);
}
Итак, у кого-нибудь есть идеи по улучшению?
3 ответов
для любого произвольного прямоугольника мы можем знать, содержит ли он белые или черные фигуры в O(1) время с O(M * N) предварительная обработка префикса матрицы-суммы для белого и черного отдельно (количество 1 для каждой части).
мы можем хранить потенциальные горизонтальные и вертикальные точки разделения отдельно в двух деревьях k-d для O(log(|splitPoints|) + k) извлечение для произвольного прямоугольника, снова предварительная обработка всего ввода.
после этого общий рекурсивный алгоритм может выглядеть например:
f(tl, br):
if storedSolution(tl, br):
return storedSolution(tl, br)
else if isValid(tl, br):
return setStoredSolution(tl, br, 0)
best = Infinity
for p in vSplitPoints(tl, br):
best = min(
best,
1 +
f(tl, (p.x-1, br.y)) +
f((p.x, tl.y), br)
)
for p in hSplitPoints(tl, br):
best = min(
best,
1 +
f(tl, (br.x, p.y-1)) +
f((tl.x, p.y), br)
)
return setStoredSolution(tl, br, best)
существует динамический подход к программированию, но он также не будет дешевым. Вам нужно заполнить загрузку таблиц, дающих для каждого размера и положения прямоугольника в главном квадрате минимальное количество делений, необходимых для полного разделения этого меньшего прямоугольника.
для прямоугольника размером 1x1 тогда ответ равен 0.
для прямоугольника размера AxB посмотрите, все ли его ячейки достаточно однородны, чтобы ответ был равен 0 для этого прямоугольника. Если так, прекрасно. Если не попробовать все возможные горизонтальные и вертикальные деления. Каждое из этих делений дает вам два меньших прямоугольника. Если вы разрабатываете ответы для всех прямоугольников размера A-1xB и меньше и размер AxB-1 и меньше, прежде чем попытаться разработать ответы для прямоугольников размера AxB вы все готовы знать ответы для двух меньших прямоугольников. Поэтому для каждого возможного деления сложите ответы для двух меньших прямоугольников и добавьте один, чтобы получить стоимость для этого деления. Выбрал подразделение, которое дает вам наименьшую стоимость, и это дает вам ответ для вашего текущего прямоугольника AxB.
разработка ответов для всех меньших прямоугольников перед большими прямоугольниками, самый последний ответ, который вы разрабатываете, дает вам оптимальное количество делений для полного квадрата. Самый простой способ выяснить, что такое лучшее деление, - это сохранить немного дополнительной информации для каждого прямоугольника, записывая, что такое лучшее деление.
для квадрата NxN есть O (N^4) прямоугольники-любые две точки в квадрате определяют прямоугольник как противоположные углы. Прямоугольник размера O(N)xO(N) имеет O(N) возможных делений, поэтому у вас есть что-то вроде алгоритма O(N^5) или O(N^2.5), если N-входной размер, так как квадрат NxN имеет входные данные размера O (N^2).
(вы также можете сделать что-то очень похожее, взяв исходный код и сохранив результаты от вызовов minBreaks () так, что если minBreaks () вызывается более одного раза с теми же аргументами, это просто возвращает сохраненный ответ вместо его пересчета с еще более рекурсивными вызовами minBreaks ()).
спасибо всем, кто помог мне, моя ошибка заключалась в том, что в этих вложенных циклах я пытался избежать некоторых ненужных перерывов, например,
1 1 -> 1 | 1
1 1 1 | 1
1 1 1 | 1
думая, что это ускорит время выполнения, но правильный подход был просто сломать плитку шоколада всегда везде, где это возможно. В любом случае для всех, кого это интересует, вот мой рабочий код:
#include <stdio.h>
#include <stdlib.h>
unsigned int M, N;
unsigned int ****pieces; ////already solved rectangles, the value of pieces[y0][x0][y1][x1] is the optimal number of pieces in which the particular rectangle(that has upperleft corner in [x0,y0] and bottomright corner in[x1,y1]) can be divided
unsigned int inf;
int isOneColor(int mat[M][N], unsigned int starti, unsigned int startj, unsigned int maxi, unsigned int maxj) {
int c = 2;
for (unsigned int i = starti; i < maxi; i++) {
for (unsigned int j = startj; j < maxj; j++) {
if (c == 2) {
if (mat[i][j] != 2) {
c = mat[i][j];
}
} else if (c != mat[i][j] && mat[i][j] != 2) {
return 0;
}
}
}
return 1;
}
unsigned int minbreaks(int mat[M][N], unsigned int starti, unsigned int startj, unsigned int maxi, unsigned int maxj) {
if (pieces[starti][startj][maxi][maxj] != 0) {
return pieces[starti][startj][maxi][maxj];
} else if (isOneColor(mat, starti, startj, maxi, maxj)) {
return pieces[starti][startj][maxi][maxj] = 1;
} else {
unsigned int currentmin = inf;
for (unsigned int j = startj; j < maxj - 1; j++) {
unsigned int c = minbreaks(mat, starti, startj, maxi, j + 1) + minbreaks(mat, starti, j + 1, maxi, maxj);
if (c < currentmin) {
currentmin = c;
}
}
for (unsigned int i = starti; i < maxi - 1; i++) {
unsigned int c = minbreaks(mat, starti, startj, i + 1, maxj) + minbreaks(mat, i + 1, startj, maxi, maxj);
if (c < currentmin) {
currentmin = c;
}
}
pieces[starti][startj][maxi][maxj] = currentmin;
return currentmin;
}
}
int main(void) {
FILE *file = stdin;
//FILE *file = fopen("inputfile", "r");
fscanf(file, "%u %u", &M, &N);
int mat[M][N];
pieces = malloc(sizeof (unsigned int***)*M);
for (unsigned int i = 0; i < M; i++) {
pieces[i] = malloc(sizeof (unsigned int**)*N);
for (unsigned int j = 0; j < N; j++) {
int x;
fscanf(file, "%d", &x);
mat[i][j] = x;
pieces[i][j] = malloc(sizeof (unsigned int*)*(M + 1));
for (unsigned int y = i; y < M + 1; y++) {
pieces[i][j][y] = malloc(sizeof (unsigned int)*(N + 1));
for (unsigned int x = j; x < N + 1; x++) {
pieces[i][j][y][x] = 0;
}
}
}
}
inf = M * N + 1; //number that is bigger by one than maximal theoretically possible number of divisions
unsigned int result = minbreaks(mat, 0, 0, M, N);
printf("%u\n", result);
return (EXIT_SUCCESS);
}