Наибольшее и наименьшее количество внутренних узлов в красно-черное дерево?
наименьшее количество внутренних узлов в красно-черном дереве с черной высотой k равно 2k-1, который является одним в следующим образом:
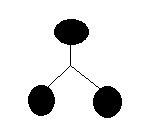
наибольшее количество внутренних узлов с черной высотой k равно 22k-1 который, если черная высота 2, должен быть 24 - 1 = 15. Однако рассмотрим этот образ:
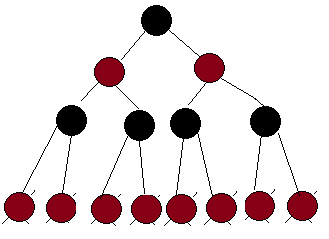
количество внутренних узлов 7. Что я делаю не так?
8 ответов
(Я полностью переписал этот ответ, потому что, как отметили комментаторы, он был изначально неверным.)
Я думаю, что это может помочь подумать об этой проблеме, используя изометрия между красно-черными деревьями и 2-3-4 деревьями. В частности, красно-черное дерево с черной высотой H соответствует 2-3-4 дерево с высотой H, в котором каждый Красный Узел соответствует одной из ключевых в нескольких ключевых узлов.
Это соединение облегчает нам сделать несколько аккуратных наблюдения. Во-первых, любой узел дерева 2-3-4 в нижнем слое соответствует черному узлу без красных детей, одного красного ребенка или двух красных детей. Это единственные узлы, которые могут быть листовые узлы красно-черных деревьев. Если бы мы хотели максимизировать количество общих узлов в дереве, мы бы хотели, чтобы дерево 2-3-4 не имело ничего, кроме 4-узлов, которые (под изометрией) сопоставляются с красным/черным деревом, где каждый черный узел имеет два красных дочерних элемента. Интересный эффект заключается в том, что слой дерева цвета чередуются между Черным и красным, причем верхний слой (содержащий корень) черный.
по существу, это сводится к подсчету количества внутренних узлов в полном двоичном дереве высоты 2h-1 (слои 2h чередуются между Черным и красным). Это равно количеству узлов в полном двоичном дереве высоты 2h - 2 (так как, если вы вытащите все листья, у вас останется полное дерево высоты на один меньше, чем вы начали). Это работает на 22h-1 - 1, который отличается от числа, которое вам дали (которое, я теперь убежден, неверно), но соответствует номеру, который вы получаете.
вам нужно подсчитать черные нулевые листья в дереве, если эта формула не будет работать. Корень не должен быть красным, что является нарушением одного из свойств красно-черного дерева.
после прочтения обсуждения выше, поэтому, если я добавлю корень с красным атрибутом, второй узел, который я добавлю, снова будет красным, что будет красным нарушением, и после реструктуризации узла я предполагаю, что мы снова достигнем корня черного и дочернего красного ! с помощью которого мы можем не получить (2^2k)-1 max внутренних узлов. Я что-то пропустил здесь , начал работать над rbt совсем недавно ...
проблема-это вы недопоняли черный высота. Черная высота узла в красно-черном дереве - это количество черных узлов от текущего узла до листа, не считая текущего узла. (Это будет одинаковое значение в каждом маршруте). Поэтому, если вы просто добавите два черных листа к каждому красному узлу, вы получите красно-черное дерево с черной высотой 2 и 15 внутренних узлов.
(тоже в красно-черном дереве каждый узел имеет два чернокожих детей, поэтому красные узлы не могут быть Лифс.)
похоже, вы не рассматривали "черные листья" (черные узлы) - 2 нулевых узла для каждого из красных узлов на последнем уровне. Если вы рассматриваете нулевые узлы как листья, красные узлы на последнем уровне теперь учитываются как внутренние узлы на общую сумму 15.
дерево, приведенное здесь, фактически имеет 15 внутренних узлов. Отсутствуют нулевые черные дочерние элементы красных узлов в последнем слое, которые фактически называются внешними узлами (узел без ключа ). Дерево черное-высота 2. Фактическое выражение для максимального числа внутренних узлов для дерева с черной высотой k равно 4^(k)-1. В этом случае, получается 15.
в красно-черных деревьях внешние узлы[нулевые узлы] всегда черные, но в вашем вопросе для второго дерева вы не упомянули внешние узлы, и, следовательно, вы получаете свой счет как 7, но если U упомянуть внешние узлы[нулевые узлы], а затем подсчитать внутренние узлы, вы можете увидеть, что это оказывается 15.
Не уверен, что понимаю вопрос. Для любого двоичного дерева, где все слои (кроме, возможно, последнего) имеют максимальное количество элементов, мы будем иметь 2^(k-1)-1 внутренних узлов, где k-количество слоев. На втором снимке у вас есть 4 слоя, поэтому количество внутренних узлов 2^(4-1)-1=7
